Постановка задач нелинейного программирования

В общем виде ЗНП формулируется следующим образом:

, (1)

, (2)

, (3)

где - управляющие переменные или решения ЗНП; - фиксированные параметры; - заданные функции от n переменных, причем целевая функция или (и) хотя бы одна из функций 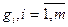являются нелинейными.

Решить задачу нелинейного программирования - это значит найти такие значения управляющих переменных , которые удовлетворяют системе ограничений (2),(3) и доставляют максимум или минимум целевой функции .

Для задачи нелинейного программирования, в отличие от линейных задач, нет единого метода решения. В зависимости от вида целевой функции (1) и ограничений (2) разработано несколько специальных методов решения, к которым относятся методы множителей Лагранжа, квадратичное и выпуклое программирование, градиентные методы, ряд приближенных методов решения, графический метод.

Процесс составления математической модели ЗНП принципиально не отличается от составления модели ЗЛП. Рассмотрим несколько примеров.

Задача 1.

На m предприятиях выпускается некоторый продукт. Себестоимость единицы этого продукта на каждом из указанных предприятий есть , где 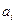- доля себестоимости, не зависящая от объема выпуска продукции, - план выпуска продукта на i-м предприятии.

Предприятия должны обеспечить n потребителей с потребностями 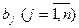, стоимость перевозки из i-го предприятия к j-му потребителю равна .

Требуется определить такой план распределения выпуска продукта предприятиями и план перевозок его потребителям, чтобы суммарная себестоимость выпуска и стоимость перевозки была минимальной.

Математическую модель задачи. Пусть - план перевозок от i-го предприятия к j-му потребителю.

Для удобства запишем данные и искомые величины задач в виде таблицы:

Потребители   Предприятия			...	n	План выпуска изделий
	x11	x12	...	x1n	x1
	x21	x22	...	x2n	x2
...
m	xm1	xm2		xmn	xm
Потребности заказчиков	b1	b2	...	bn

 

Система ограничений задачи:

(4)

Целевая функция f запишется так: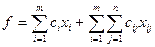

Вместо подставим значения, данные в условии задачи:

(5)

Надо найти минимальное значение функции (5) на множестве допустимых решений (4).

Задача 2.

На производство некоторого продукта расходуется два вида ресурсов. Определите оптимальное распределение величин затрачиваемых ресурсов, если цена ресурса первого вида 30 рублей, второго - 40 рублей, а всего выделено на производство 120 рублей. Известно, что из количества x₁ первого ресурса и x₂ второго ресурса можно получить единиц продукта.

Вообще, функция выражающая зависимость между количеством вырабатываемого продукта и величиной расходуемых на него ресурсов, называется производственной функцией. Простейшая производственная функция для продукта, получаемого из двух различных ресурсов имеет вид:

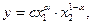
где - постоянные величины, причем

Функция y выведена в предположении, что существует только два ресурса: x₁ - труд, x₂ - капитал, где указывает на соответствующую долю использования каждого из этих ресурсов; c - некоторый постоянный коэффициент; y - это количество совокупного продукта, которое при определенных технологических условиях может быть получено из данных продуктов. Функция y простейшая производственная функция, так как рассматривает зависимость между двумя ресурсами и одним продуктом.

Математическая модель задачи. Пусть x₁ - количество ресурсов вида 1, x₂ - количество ресурсов вида 2. Система ограничений:

(6)

Целевая функция:

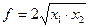(7)

Требуется найти наибольшее значение функции (7) на множестве решений системы (6).

⇐ Предыдущая6789101112131415Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: