Примеры решения типовых задач

Пример 1.

Имеются следующие данные о цене на нефть х (усл.ед) и индексе акций нефтяных компаний у (усл.ед).

Таблица 3

хi	17,3	17,0	18,3	18,8	19,2	18,5
yi

Предполагая, что между переменными х и у существует линейная зависимость, найти эмпирическую формулу y=ɑх + b методом наименьших квадратов.

Решение.

Перепишем таблицу в виде столбцов и проведем необходимые вычисления.

Таблица 4

n	xi	yi	xi2	xiyi
	17,3		299,29	9290,1
	17,0		289,00	9078,0
	18,3		334,89	10065,0
	18,8		353,44	10434,0
	19,2		368,64	10752,0
	18,5		342,25	10212,0
∑	109,1		1987,51	59831,1

Составим систему уравнений:

1987,51ɑ + 109,1 b = 59 831,1

109,1 ɑ + 6 b = 3288

 

Откуда ɑ=11,946, b=330,78, т.е

y = 11,94 x + 330,78.

Пример 2.

Найти квадратичную зависимость для следующих данных. Предприятие, производящее сельскохозяйственную технику, провело опрос дилеров и получила следующие сведения о спросе Q на свою продукцию в зависимости от цены P:

Таблица 5

P = х, млн. руб	1,7	1,9	2,0	2,1
Q = y, тыс. штук

 

Решение.

Перепишем таблицу в виде столбцов и проведем необходимые вычисления.

Таблица 6

п	xi	yi	xi2	xi3	xi4	xi yi	xi2 yi
	1,7		2,89	4,913	8,3521	45,9	78,03
	1,9		3,61	6,859	13,0321	47,5	90,25
	2,0		4,00	8,000	16,0000	38,0	76,00
	2,1		4,41	9,261	19,4481	18,9	39,69
∑	7,7		14,91	29,033	56,8323	150,3	283,97

Система линейных уравнений для определения величин ɑ, b, спримет вид

56,8323ɑ + 29,0330 b + 14,9100с = 283,97,

29,0330 ɑ + 14,9100 b + 7,7000с = 150,30,

14,9100 ɑ + 7,7000 b + 4 с = 80,00.

 

 

Решив систему, получим значения ɑ, b, с. Функция спроса будет иметь вид Q = 0,02 Р² - 16.64 Р - 6,67.

Пример 3.

Имеются следующие данные о величине пробега автомобиля х (тыс.км) и у – расходе масла (л/тыс.км):

 

Таблица 7

хi
yi	0,2	0,5	0,8	1,1	1,3

Полагая, что между переменными х и у существует линейная зависимость, найти эмпирическую формулу у=ɑх + b методом наименьших квадратов.

Решение.

Перепишем таблицу в виде столбцов и проведем необходимые вычисления.

Таблица 8

n	xi	yi	xi2	xiyi
		0,2
		0,5
		0,8
		1,1
		1,3
∑		3,9

Система нормальных уравнений имеет вид:

 

44500ɑ + 450b = 407

450ɑ + 5b = 3,9

 

Ее решения ɑ=0,014, b = -0,48. Таким образом, линейная зависимость имеет вид: y= 0,014x – 0,48

 

Пример 4.

Имеются следующие данные о расходах на рекламу x (тыс. усл.ед.) и сбыте продукции (тыс. ед.):

Таблица 9

хi
yi	1,6	4,0	7,4	12,0	18,0

 

Предполагая, что между переменными x и y существует квадратичная зависимость вида y = ɑx² + bx + c, найти значения параметров ɑ, b, c методом наименьших квадратов.

Перепишем таблицу в виде столбцов и проведем необходимые вычисления.

Таблица 10

n	xi	yi	xi2	xi3	xi4	xiyi	xi2 yi
		1,6 4,0 7,4 12,0 18,0				1,6 8,0 22,2 48,0 90,0	1,6 16,0 66,6 196,0 450,0
∑		43,0				169,8	680,2

Система нормальных уравнений имеет вид:

979ɑ + 225b + 55с = 680,2,

225 ɑ + 55b + 15 с = 169,8,

55 ɑ + 15 b + 5 с = 49,0.

Её решения ɑ=0,3, b=0,48, c=5,06.

Искомая зависимость имеет вид: y= 0,3x² + 0,48x +5,06.

 

Пример 5.

Имеется шесть измерений пары переменных (х,у) результаты которых приведены в таблице 11:

Таблица 11

xi
yi	0,2	0,3	1,0	1,2

 

Методом наименьших квадратов построить линейную зависимость у=ɑх + b. Сравнить полученную зависимость с зависимостью у= .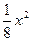

Решение.

Аналогично примерам 1,3 найдем уравнение линейной регрессии:

у= 0,37х – 0,25.

Сравним величины U = для найденной линейной зависимости и зависимости у= 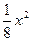. Промежуточные вычисления представим в таблице:

Таблица 12

n	xi	yi		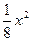0,37хi– 0,25	( - yi)2	(0,37xi – 0,25 – уi)2
		0,2 0,3 1,0 1,2	0,125 0,5 1,125	0,12 0,49 0,76 1,23	0,005625 0,040000 0,015625 0,640000	0,0064 0,0361 0,0576 0,0009
∑	-	-	-	-	0,701250	0,1010

 

Как видно U_лин< U_кв, следовательно, линейная зависимость предпочтительнее.

Задания для работы в аудитории

I. Имеются следующие данные о величинах x и y. Предполагая, что между

x и y существует линейная зависимость, найти эмпирическую формулу

у=ɑх + b методом наименьших квадратов.

Задача 1.

х – цена на товар (усл.ед.); у – уровень продаж (тыс.ед.):

 

Таблица 13

xi	3,0	4,0	5,0	6,0	7,0
yi

 

Задача 2.

х – уровень потребления электроэнергии на предприятии (млн.кВт ^. ч); у – себестоимость единицы продукции:

 

Таблица 14

xi
yi

 

 

II. По экспериментальным данным построить методом наименьших квадратов линейную зависимость у=ɑх + b. Сравнить полученную зависимость с альтернативной и определить, какая из них лучше соответствует экспериментальным данным.

 

Задача 3.

Таблица 15

xi		2,5		3,5
yi	4,2	5,5	6,9		9,5

 

Альтернативная зависимость y=2x + 0,1x².

 

Задача 4.

Таблица 16

xi
yi	1,0	1,4	1,7	2,0	2,2

 

Альтернативная зависимость y=

 

Задача 5.

Таблица 17

xi	1,0	1,5	2,0	2,5	3,0
yi	0,50	0,30	0,25	0,18	0,12

 

Альтернативная зависимость y=2^-х

⇐ Предыдущая891011121314151617Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: