Некоторые типы эмпирических формул

В практических применениях математики очень часто встречается такая задача. Зависимость между переменными величинами выра­жается в виде таблицы, полученной опытным путем. Это могут быть результаты эксперимента, данные наблюдений или измерений, ста­тистической обработки материала. Например, зависимости пути, пройденного телом, от времени; данные о цене на пшеницу и индексы акций перерабатывающих пшеницу компаний; прибыли предприятия по годам деятельности предприятия; динамики прироста массы сельскохозяйственных животных от количества кормов и т.п.

Пусть дана эмпирическая зависимость.

Таблица 1

X	x1	x2	…	xi	…	xn
У	y1	y2	…	yi	…	yn

Требуется выразить зависимость между переменными аналитически, т. е. дать формулу, связывающую между собой соответствующие значения переменных. Такая формула очень облегчает анализ изучаемой зависимости. Формулы, служащие для аналитического представления опытных данных, принято называть эмпирическими формулами.

Задача нахождения эмпирических формул заключается в следующем:

1) устанавливается вид зависимости y = f(x), т.е устанавливется, является ли она линейной, квадратичной, логарифмической или какой-либо другой, которая содержит ряд числовых параметров ɑ, b, c, …;

2) определяются неизвестные параметры функции, так чтобы кривая

y = f(x) наилучшим образом изображала зависимость, полученную в опыте.

Пусть результаты экспериментальных исследований нанесены на плоскость, паре чисел (x_i, y_i) соответствует точка с такими же координатами. Разумеется, существует множество кривых, проходящих через эти точки (см.рисунок 1).

 

Рисунок 1.

Предполагают, что кривая истиной зависимости – наиболее гладкая кривая (пунктир), согласованная с эмпирическими данными, поэтому именно ее предпочтет исследователь. Однако, для проверки правильности вывода проводится еще ряд одновременных измерений величин x и y. Дополнительные точки наносятся на плоскость. Если они оказываются достаточно близкими к выбранной кривой, то можно считать, что вид кривой установлен.

Кроме того, многих случаях характер зависимости между переменными величинами определяется из каких-либо теоретических соображений не математического характера (например, используя опыт предшествующих исследований). Например, известно, что при свободном падении тела в пустоте зависимость пути от времени дается формулой: s= .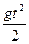

Здесь g —коэффициент пропорциональности, являющийся ускорением силы тяжести; его значение находится из опыта.

Измеряя фактически пройденный телом путь в разные моменты времени, мы получаем таблицу соответствующих значений перемен­ных t и s. Задача состоит теперь в том, чтобы, исходя из наблю­даемых значений, подобрать подходящее значение g. Если бы данные наблюдения были точными, то для нахождения величины g достаточно было иметь одно значение t и соответствующее значение s. Но полученные значения s содержат ошибки измерений и из каждого наблюдения будет получаться другое значение s; нужно подобрать значение s таким, чтобы оно наилучшим образом удовлетворяло всем наблюдениям.

Еще чаще приходится встречаться с более общей и более слож­ной задачей: в результате наблюдений получен ряд значений пере­менных х и у, однако истинный характер функциональной зависи­мости между ними остается неизвестным.

Здесь мы можем ставить перед собой цель подобрать какую-либо формулу, наилучшим образом отображающую полученные результаты. Применяются два различных метода построения таких формул. Один из них состоит в том, что строится многочлен, принимающий в заданных точках заданные значения, а именно: по двум известным точкам строится линейная функция (прямая), по трем - квадратич­ная (парабола) и т. п. Достоинство этого метода в том, что полу­ченная формула в точности воспроизводит заданные значения. Такого рода формулы носят название интерполяционных формул.

Другой метод подбора эмпирических формул состоит в том, что по данным результатам наблюдений подбирается наиболее простая формула того или иного типа, дающая наилучшее приближение к имеющимся данным. При этом формула не воспроизводит в точ­ности данных наблюдения, но этого и нет смысла требовать, учиты­вая, что полученные результаты могут содержать ошибки измерений.

Прежде чем переходить к вопросу о выборе типа подходящей формулы и подборе параметров, нужно уточнить, что следует пони­мать под словами «наилучшее совпадение с имеющимися данными». Этим словам можно придавать различный смысл, и тогда мы будем получать различные формулы для одних и тех же результатов наблюдений. Каждая из них будет в своем смысле «наилучшей».

Чаще всего при подборе эмпирических формул пользуются так называемым методом (принципом) наименьших квадратов. Он основан на том, что из данного множества формул вида у=f(х) наилучшим образом изображающей данные значения считается та, для которой сумма квадратов отклонений наблюдаемых значений от вычисленных является наименьшей.

Подбор параметров функции f (х), основанный на этом методе, называют способом наименьших квадратов.

Необходимо помнить, что способ наименьших квадратов приме­няется для подбора параметров после того, как вид функции у = [(х) определен. Если из теоретических соображений нельзя сделать никаких выводов о том, какой должна быть эмпирическая формула, то приходится руководствоваться наглядными представлениями, прежде всего графическим изображением наблюденных данных. Вид функции у = f(х) выбирается таким образом, чтобы график этой функции по возможности близко напоминал расположение на гра­фике данных наблюдения.

Покажем, как практически подбираются по способу наименьших квадратов коэффициенты для функций простейших видов. Ограни­чимся следующими видами функций: линейная функция, квадратичная функция, гипербола и показательная функция.

1) вида у = ах + b,

2) вида у = ах² + bх+с,

3) вида у = а+ ,

4) вида у= а ^. b ^х.

1) Линейная функция вида у = ах + b.

Пусть задана таблица 2 значений переменных и соответствующие

Таблица 2

x1	хг	…	xn-1	xn
y1	y2	…	yn-1	yn

точки располагаются вблизи прямой линии (рис. 2). В этом слу­чае нужно подбирать коэффициенты линейной функции у = ах + b

Рисунок 2.

 

 

так, чтобы сумма квадратов отклонений вычисленных значений ах_i + b от наблюдаемых значений у_i т. е. величина

U = (ах₁ + b - у₁)²+ (ах₂ + b—у₂)² +...+ (ах_n +b – у_п)²,

принимала наименьшее значение.

Сумма U= (ах_i +b – у_i)²

является функцией двух переменных а и b, а поэтому она прини­мает минимальное значение при тех значениях а и b, при которыхобращаются в нуль частные производные этой функции по каждой переменной, т. е. когда:

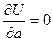и

 

Находим частные производные:

 

;

 

.

 

Приравнивая каждую частную производную нулю, получаем систему двух линейных уравнений относительно a и b

(1)

2) Квадратичная функция, вида: у = ах² + bх+с.

В случае квадратичной функции следует рассматривать сумму:

U= ,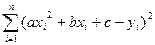

которая является функцией трех переменных a, b и c, а поэтому принимает минимальное значение при тех значениях a, b и c, при которых обращаются в нуль частные производные этой функции по каждой переменной, т.е когда

 

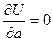, и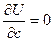

 

Находим частные производные

;

.

.

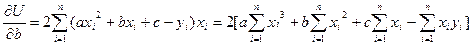Приравниваем каждую частную производную нулю, получаем нормальную систему:

,

,

.

3) Гипербола вида у = а+ b/x.

Применение метода наименьших квадратов приводит к рассмотрению суммы вида

 

U =

Являющейся функцией двух переменных параметров a и b.

Отыскание частных производных дает

 

 

 

Вводя условия экстремума 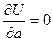и , получаем

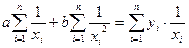или

и

или

nɑ + b .

Отсюда можно записать нормальную систему для определения параметров

a и b.

nɑ + b ,

.

4) Показательная функция, вида y = ɑ ^. b^x.

Используется логарифмическое преобразование функции y=ɑb^x к виду

lny = ln(ɑb^x) = xlnb + lnɑ,

выражающему lny как линейную функцию от x при параметрах lnɑ и lnb.

Определение этих параметров связывается здесь с отысканием по способу наименьших квадратов минимума суммы вида:

U =

Из условий

и .

Эти условия приводят к нормальной системе, которая по структуре своей аналогична системе, полученной в первом случае для линейной функции:

lnb ,
lnb .

 

Найденные из этой системы значения lnɑ и lnb позволяют легко с помощью таблиц логарифмов или калькулятора определить значения ɑ и b.

 

⇐ Предыдущая891011121314151617Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: