Особенности решения задач нелинейного программирования

Для решения ЗНП существенно знать: 1) выпукло или не выпукло множество допустимых решений задачи; 2) является ли целевая функция выпуклой или вогнутой или она не относится ни к тому, ни к другому классу.

Говорят, что множество выпукло, если оно вместе с любыми своими точками А и В содержит и все точки отрезка АВ. Примерами выпуклых множеств в пространстве могут служить сфера, пирамида, призма и т.д. В невыпуклом множестве можно указать хотя бы две точки, такие, что не все точки отрезка АВ принадлежат рассматриваемому множеству. Примером невыпуклого множества в пространстве является тор.

Функцию y = f(x) одной переменной будем называть выпуклой, если отрезок, соединяющий две любые точки ее графика, принадлежит графику или расположен выше его. Функция вогнута, если отрезок, соединяющий две любые точки графика, принадлежит ему или расположен ниже его.

Аналогично можно сформулировать определения понятий вогнутой и выпуклой функций нескольких переменных. Говорят, что гиперповерхность z=f(x₁,x₂,...,x_n) выпуклая, если отрезок, соединяющий две ее любые точки, лежит на поверхности или выше ее. Гиперповерхность z=f(x₁,x₂,...,x_n) вогнута, если отрезок, соединяющий две ее любые точки, лежит на поверхности или ниже ее. Пусть дана функция , определенная на замкнутом множестве Ф. Элементами множества Ф являются точки . Поэтому функцию можно записать так: .

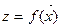Говорят, что функция 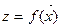, определенная на некотором множестве X, достигает в точке локального максимума (локального минимума), если найдется такое число , что для всех , удовлетворяющих неравенству , выполняется неравенство

Точка , в которой функция достигает локального максимума (минимума), называется точкой локального максимума (минимума).

Пусть функция 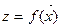определена на замкнутом множестве X. Если и для любой точки , то говорят, что в точке функция достигает глобального максимума (глобального минимума).

Точка , в которой все частные производные функции 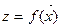равны 0, называется стационарной точкой.

Необходимое условие экстремума. Если в точке функция 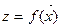имеет экстремум, то частные производные функции в этой точке равны нулю:

.

Как и в случае одной переменной, необходимое условие не является достаточным для того, чтобы стационарная точка была точкой экстремума. Для получения достаточных условий следует определить в стационарной точке знак дифференциала второго порядка. Дифференциал второго порядка обозначается и равен сумме произведений частных производных второго порядка на соответствующие приращения аргументов. Если от частной производной найти частную производную по переменной , то получим частную производную второго порядка по переменным , которая обозначается . В этом случае

.

Достаточные условия экстремума:

а) в стационарной точке функция 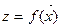имеет максимум, если 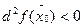, и минимум, если , при любых и , не обращающихся в нуль одновременно;

б) если может принимать в зависимости от и и положительные, и отрицательные значения, то в точке экстремума нет;

в) если может обращаться в нуль не только при нулевых приращениях и , то вопрос об экстремуме остается открытым.

Для функции двух переменных достаточные условия не очень сложны. Существуют четыре частные производные второго порядка:

Найдем значения частных производных второго порядка в стационарной точке :

 

Обозначим через определитель, составленный из

(8)

Тогда достаточные условия экстремума функции двух переменных имеют вид:

а) если >0 и a₁₁<0 (a₂₂<0), то в точке функция имеет максимум; если >0 и a₁₁>0 (a₂₂>0), то в точке функция имеет минимум;

б) если <0, то экстремума нет;

в) если , то вопрос об экстремуме остается открытым.

Если область Ф замкнута и ограничена, то дифференцируемая функция 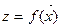достигает в этой области своих наибольшего и наименьшего значений или в стационарной точке, или в граничной точке области.

Таким образом, чтобы найти наибольшее (наименьшее) значение функции 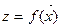в области Ф, нужно:

1) найти все стационарные точки внутри области Ф и вычислить значения функции в них:

2) исследовать функцию на экстремум на границе области Ф;

3) сравнить значения функции, полученные в п.1 и п.2: наибольшее (наименьшее) из этих чисел и будет наибольшим (наименьшим) значением функции во всей области.

Граница области Ф аналитически может быть задана системой уравнений (условий) относительно переменных . Поэтому, исследуя экстремальные свойства функции на границе, необходимо решить задачу определения условного экстремума.

Условный экстремум. Пусть необходимо найти экстремум функции 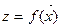при условии, что переменные удовлетворяют уравнениям:

)=0, (9)

Предполагается, что функции и имеют непрерывные частные производные по всем переменным. Уравнения (6.9) называются уравнениями связи.

Говорят, что в точке 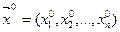, удовлетворяющей уравнениям связи (6.9), функция 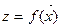имеет условный максимум (минимум), если неравенство имеет место для всех точек , координаты которых удовлетворяют уравнениям связи.

Для задач линейного программирования характерно следующее:

Множество допустимых решений выпукло. Это выпуклое множество имеет конечное число вершин, называемых обычно крайними (угловыми(точками.

Множество всех точек n-мерного пространства, в которых целевая функция принимает заданное значение, есть гиперплоскость (линия) уровня. Кроме того, гиперплоскости, соответствующие разным значениям целевой функции, параллельны.

Локальный max или min является также глобальным max или min целевой функции на множестве допустимых решений, т.е. не существует локального оптимума целевой функции, отличного от глобального оптимума.

Если оптимальное значение целевой функции ограничено, то по крайней мере одна крайняя точка множества допустимых решений является оптимальным решением. Кроме того, начав с произвольной вершины множества допустимых решений, можно достичь оптимума за конечное число шагов, причем на каждом шаге совершается переход только в соседнюю вершину. Окончательно данная вершина является оптимальной тогда и только тогда, когда значение целевой функции в ней по крайней мере не меньше, чем значения целевой функции во всех примыкающих вершинах.

У произвольной задачи нелинейного программирования некоторые или все приведенные выше свойства ЗЛП отсутствуют. Поэтому ЗНП гораздо сложнее задач линейного программирования и для них не существует общего универсального метода решения (аналогично симплексному методу).

Метод множителей Лагранжа

Среди задач (1)-(3) особое место занимают задачи типа

(10)

, (11)

для решения которых можно воспользоваться классическим методом оптимизации Лагранжа, или методом разрешающих множителей. При этом предполагают, что функции и непрерывны вместе со своими первыми частными производными.

Можно указать следующий порядок решения задачи (10)-(11) методом множителей Лагранжа:

1) составить функцию Лагранжа:

L (12)

здесь - множители Лагранжа;

2)Найти частные производные функции Лагранжа по всем переменным и приравнять их нулю. Тем самым получим систему:

(13)

 

Эта система состоит из m + n уравнений. Решить эту систему (если это окажется возможным) и найти таким образом все стационарные точки функции Лагранжа;

3) из стационарных точек, взятых без координат выбрать точки, в которых функция f( имеет условные локальные экстремумы при наличии ограничений (11). Этот выбор осуществляется, например, с применением достаточных условий локального экстремума. Часто исследование упрощается, если использовать конкретные условия задачи.

В основе метода Лагранжа решения классической задачи оптимизации (10)-(11) лежит утверждение, что если в точке 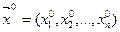имеет экстремум, то существует такой вектор , что точка

является решением системы (13). Следовательно, решая систему (13), получаем множество стационарных точек, в которых функция Z может иметь экстремальные значения. При этом, как правило, неизвестен способ определения точек глобального максимума или минимума. Однако, если решения системы найдены, то для определения глобального экстремума достаточно найти значения функции в соответствующих точках области определения.

Множителям Лагранжа можно придать следующий экономический смысл. Если - доход, соответствующий плану , а функция 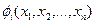- издержки i-го ресурса, соответствующие этому плану, то - цена (оценка) i-го ресурса, характеризующая изменение экстремального значения целевой функции в зависимости от изменения размера i-го ресурса.

Пример.По плану производства продукции предприятию необходимо изготовить 200 изделий. Эти изделия могут быть изготовлены двумя технологическими способами. Производственные затраты на изготовление n изделий первым способом равны 4n+n², а для второго способа - 8n+n². Сколько изделий надо изготовить каждым способом, чтобы общие затраты на производство продукции были бы минимальными.

Обозначим число изделий, изготовленных первым способом через х₁, вторым способом - х_2. Тогда суммарные затраты на изготовление продукции по плану составят:

f (x₁,x₂)=4x₁+x₁²+8x₂+x₂²

При этом общее число изделий должно быть равно 200, т.е.

x₁+x₂=200.

Получим математическую модель задачи:

f(x₁,x₂)=4x₁+x₁²+8x₂+x₂²

x₁+x₂=200

x₁ x₂ .

Для ее расчета применим метод множителей Лагранжа.

Составим функцию Лагранжа

L(x_1,x₂, )=4x₁+x₁²+8x₂+x₂²+ (200-x₁-x₂).

Найдем частные производные функции L по x₁,x₂, и приравняем их к нулю:

.

имеем систему:

.

Исключим из этой системы , например выразим из первого уравнения и подставим найденное значение во второе уравнение системы, получим:

.

Таким образом, по необходимому условию экстремума дифференцируемой функции получим стационарную точку М(101,99) возможного условного экстремума функции f(x₁,x₂).

Дальнейшее исследование этой точки будем проводить как и в случае безусловного экстремума.

Найдем частные производные второго порядка:

.

Для рассматриваемого примера производные постоянны и не зависят от значений х₁ и х₂. Поэтому a₁₁=2, a₁₂=a₂₁=0, a₂₂=2 (см. 6.8). Вычислим определитель

.

Так как определитель больше нуля и a₁₁=2>0, следовательно, в точке М(101,99) функция f(x₁,x₂) имеет минимум:

(ед.).

При изготовлении 101 детали первым способом и 99 деталей вторым способом затраты на производство будут минимальными и равными 21198 денежным единицам.

⇐ Предыдущая78910111213141516Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: