Подбор эмпирических формул по выборочным данным

Прибыль предприятия за некоторый период деятельности по годам приведена ниже. Год: x_i, прибыль (млн. руб): y_i.

Таблица 18

xi	yi
	3,5

Требуется подобрать тип зависимости, используя метод наименьших квадратов, исходя из условия минимума суммы квадратов отклонений. Сделать чертеж одной из наиболее подходящих зависимостей, нанести на график исходные данные.

 

1.Линейная зависимость: у=ax+b.

Запишем нормальную систему для определения параметров ɑ и b зависимости: у = ɑx + b

D_i= y_расч - y_i..

Таблица 19

i	xi	yi	xi2	xiyi	yiрасч	Di	Di2
					4,79	0,21	0,0441
					4,33	-0,33	0,1089
		3,5			3,41	0,09	0,0081
S		12,5					0,1611

ɑ» -0,46; b» 5,25

y = - 0,46х + 5,25.

Вычисляем y_iрасч :

x₁= 1; y_1расч=-0,46×1+5,25=4,79

x₁= 2; y_{2 расч} =-0,46×2+5,25=4,33

x₁= 4; y_{3 расч} =-0,46×4+5,25=3,41.

 

2. Квадратичная зависимость: y = ax² + bx + с.

Запишем нормальную систему для определения параметров ɑ, b и c данной зависимости:

,

, D_i= y_расч - y_i.

,

Таблица 20

i	xi	yi	xi yi	xi2	xi2 yi	xi3	xi4	yiрасч	Di	Di2
		3,5						3,5
S		12,5

 

ɑ = 0,25; b = -1,75; c = 6,5

y = 0,25x² - 0,75x + 6,5

Вычисляем y_iрасч:

x₁=1; y_1расч =0,25× 1² – 1,75 1 + 6,5 =5

x₂=2; y_2расч =0,25× 2² - 1,75 2 + 6,5 =4

x₃=4; y_3расч =0,25× 4² - 1,75 4 + 6,5 =3,5.

3. Дробно-линейная зависимость: y = ɑ + .

Запишем нормальную систему для определения параметров ɑ и b данной зависимости:

D_i= y_расч - y_i.

Таблица 21

i	xi	yi	xi2	1/xi	1/xi2	yi /xi	yiрасч	Di	Di2
				0,5	0,25
		3,5		0,25	0,0625	0,875	3,5
S		12,5		1,75	1,3125	7,875

 

a=3; b=2

y=3 + .

Вычисляем y_iрасч:

x₁=1; y_1расч =3 + = 5

x₂=2; y_2расч =3 + = 4

x₃=4; y_3расч =3 + =3,5

4. Показательная зависимость: y = ɑ × b^x

Запишем нормальную систему для определения параметров ɑ и b данной зависимости:

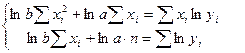
D_i= y_расч - y_i.

Таблица 22

i	xi	yi	xi2	lnyi	xi lnyi	yiрасч	Di	Di2
				1,61	1,61	4,86	0,14	0,0196
				1,39	2,78	4,37	-0,37	0,1369
		3,5		1,25		3,54	-0,04	0,0016
S		12,5		4,25	9,39			0,1581

 

lnb=-0,11; b=e^-0,11»0,9; lna=1,68; a=e^1,68»5,4

y = 5,4×0,9^x

Вычисляем y_iрасч:

 

x₁=1; y_1расч =5,4× 0,9¹»4,86

x₂=2; y_2расч = 5,4× 0,9²»4,37

x₃=4; y_3расч =5,4× 0,9⁴»3,54

 

Суммы квадратов отклонений расчетных данных от теоретических данных для найденных зависимостей записаны в табл.23.

 

Таблица 23

i	Зависимость	åDi2
	y=-0,46х+5,25	0,1611
	y=0,25x2-0,75x+6,5
	y=3 +
	y=5,4×0,9x	0,1581

ВЫВОД: Наилучшим образом подходит дробно-линейная зависимость (y=3 + ) и квадратичная зависимость (y=0,25x²-0,75x+6,5).

Сделаем чертеж одной из наиболее подходящих зависимостей, нанесем на график исходные данные.

 

 

Задание для самостоятельной работы

 

Задача.

В ходе исследования покупательского спроса, получены следующие данные, где х – цена товара, а y – количество товара. Требуется подобрать тип зависимости, используя метод наименьших квадратов, исходя из условия минимума суммы квадратов отклонений. Сделать чертеж одной из наиболее подходящих зависимостей, нанести на график исходные данные.

 

№1

xi	yi
-1
	1.5

 

№2

xi	yi
-1	-2

 

№3

xi	yi
-1
	-1

№4

xi	yi
-1	-1
0.5

 

№5

xi	yi
-2	-4
-1	-1

 

№6

xi	yi
-1
	1.5

 

№7

xi	yi
-1	-2

 

№8

xi	yi
-1
0.5

 

№9

xi	yi
-1	0.5

 

№10

xi	yi
-2
-1

 

№11

xi	yi
-1	-1

 

 

№12

xi	yi
-1
0.5

 

№13

xi	yi
-1
0.5

 

№14

xi	yi
-1

 

№15

xi	yi
-2	-5/2
-1	-3/2
	-1/2

 

№16

xi	yi
-1	-2
	-1

 

№17

xi	yi
-1
	-1

4 Элементы сетевого планирования

 

Многие проекты: строительство здания или другого сооружения, выполнение крупных ремонтных работ, разработка и создание сложной системы оружия, изготовление крупной единицы оборудования и выполнение научно-исследовательской или опытно-конструкторской работы имеют ряд общих характеристик:

1. Проекты состоят из хорошо определенной совокупности работ, выполнение которых означает завершение проекта.

2. Работы упорядочены таким образом, что они должны выполняться в определенной последовательности.

3. Продолжительность выполнения каждой работы известна заранее либо может быть оценена достаточно точно.

4. Предполагается, что начатая работа продолжается без перерыва до завершения.

5. Выполнение последующей работы не обязательно должно начинаться сразу же после завершения непосредственно предшествующей ей, однако она не может начинаться, пока не будет завершена предыдущая работа.

При управлении такими проектами применяются специальные способы изображения сетей, позволяющие разработать очень эффективные и простые процедуры вычислений информации о состоянии проекта.

 

Построение сетевой модели

Для полного описания проекта необходимо:

1. Задать список работ, входящих в проект, S={s₁,s₂,…,s_n}, и длительность их выполнения t(s_i).

2. Задать для каждой работы s_iÎS список непосредственно предшествующих ей работ Г^-1(s_i).

При анализе комплекса работ возникает задача определения минимальной продолжительности проекта и отвечающего ему плана выполнения работ. Наиболее простой метод решения этой задачи получаем, используя представление проекта в виде сети.

Сетевая модель проекта представляет собой графическое описание плана, показывающее взаимосвязь между всеми работами, выполнение которых необходимо для завершения проекта. Сеть состоит из ориентированных дуг, соединяющих пару узлов. Дугам сети отвечают работы. Узлы являются событиями. Событие выступает связующим звеном между предшествующими и последующими работами. Оно представляет собой момент свершения одной или большего числа работ и может быть отправным моментом для начала последующих работ.

Каждая дуга имеет определенную ориентацию и вес, равный затратам времени на выполнение работы, соответствующей этой дуге. Любая работа не может начинаться раньше, чем будут завершены все предыдущие работы. Сеть проектаявляется бесконтурной. В сети может быть только одно событие, определяемое моментом начала исполнения проекта, и одно событие, которому отвечает момент завершения проекта.

Направление дуги определяет соотношения предшествования. На отрезке сети

i-е событие должно произойти до начала работы А. Аналогично, j-е событие не может произойти до завершения работы А.

Отношение предшествования между узлами является транзитивным. Если i-е событие предшествует j-му событию, а j-е событие предшествует k-му событию, то i-e событие предшествует k-му событию:

Иногда отношение предшествования между работами нельзя представить точно с помощью обычной структуры работ и событий. Тогда предлагается вводить фиктивные работы нулевой продолжительности и фиктивные события.

	Неправильное представление предшествования.		Сетевая модель с фиктивной работой.

 

Рисунок 1. Рисунок 2.

 

Допустим, например, что фрагмент сетевой модели, показанный на рис. 1, соответствует такой последовательности выполнения работ: работа G следует за работами В и С, и работа Е следует за работой В (но не за работойС)]. Очевидно, что тогда схема на рис.1 является неправильной, поскольку она показывает, что как работа G, так и работа Е следуют за работами С и В. Чтобы получить правильное представление, необходимо ввести фиктивную работу, продолжительность которой равна нулю. Фиктивная работа обозначена штрихпунктиром. Правильное представление дано на рис. 2, где через X обозначена фиктивная работа. При необходимости фиктивные работы могут использоваться для изображения соотношений между работами, которые невозможно представить другим способом. Введение в проект фиктивных работ - это прием, позволяющий показать требуемое соотношение без изменения фактической продолжительности проекта. Для иллюстрации построения сетевой модели рассмотрим следующий пример.

Пример 1.

Требуется построить сетевой график проекта. Информация о проекте представлена в таблице 1.

Таблица 1

Работа si	Продол-житель-ность работы	Непосред-твенно предшеству-ющие работы
Обозна-чение	Описание	t(si)	Г-1(si)
A	Закупка деталей для узла 1		Нет
B	Закупка деталей для узла 2		Нет
C	Закупка деталей для узла 3		Нет
D	Изготовление узла 1		A
E	Изготовление узла 2		B
F	Изготовление узла 4		D,E
G	Изготовление узла 3		C,D
H	Сборка		F,G
I	Проверка и испытание		H

Сетевой график, соответствующий проекту, изображен на рис.3. В нем буквами X и Y обозначены фиктивные работы, наличие которых здесь обязательно. Действительно, если убрать дугу X, то получим сеть для проекта, в котором работе G непосредственно предшествуют работы E,D,C. Однако, это не соответствует проекту, описанному в таблице 1. Аналогичный результат получим, исключив фиктивную дугу Y: работе F будут непосредственно предшествовать работы E,D,C.

Сетевой график для примера 1.

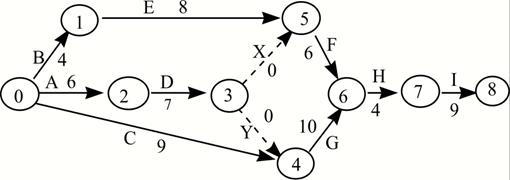Рисунок 3.

Около каждой дуги указаны имя соответствующей работы и ее продолжительность.

Для построения наиболее эффективного метода анализа сети требуется определить правильную нумерацию событий.

Нумерация событий сети называется правильной, если каждая дуга исходит из узла с меньшим номером, чем входит.

События сети на рис.3 имеют правильную нумерацию.

При большом размере сети определение правильной нумерации событий может вызвать затруднения.

Алгоритм правильной нумерации событий.

Начинаем просмотр сети с начального события (узла, для которого Г^-1(s_i)=Æ), которому присваиваем номер 1 и считаем событием 0-го ранга. Полагаем i =0, k₀=0.

Вычеркиваем все дуги, исходящие из событий i-го ранга. Если таких дуг нет, переходим к шагу 4.

События s¢, для которых Г^-1(s¢)=Æ, объединяем в группу событий (i+1)-го ранга и присваиваем им в произвольном порядке номера k_i+1,k_i+2,k_i+3,…,k_i+1. Увеличиваем i на единицу и переходим к шагу 2.

Конечной целью анализа сетевой модели является получение инфор­мации о плановых сроках выполнения отдельных работ. Остановимся на решении этой задачи методом критического пути (МКП).

 

⇐ Предыдущая891011121314151617Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: