Особенности движения автомобиля на кривой

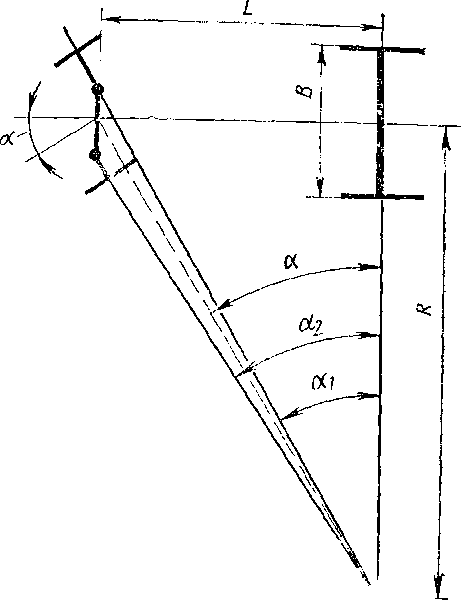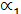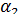При движении автомобиля по кривой все четыре его колеса двигаются по дугам окружности разных радиусов, при этом про­должение передней и задней осей колес автомобиля пересекается в одной точке (рис. 13). Поскольку разница между углами и невелика, то в расчет принимается средний для обоих колес угол поворота α, который может быть определен по про­стейшей формуле .

 

Рис.13 Схема поворота автомобиля

 

Очевидно, угол поворота 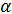, следовательно, и угловое ускоре­ние тем больше, чем меньше радиус поворота.

Движение автомобиля по кривой весьма сложно, так как, кроме положения осей, на движение оказывают значительное воздействие колебания рессор, распределение нагрузок между колесами, скорость поворота передних колес, деформации шин и другие причины.

Рассмотрим условие устойчивости движущегося автомобиля по наклонной поверхности проезжей части дороги на кривой (рис. 14).

 

 

 

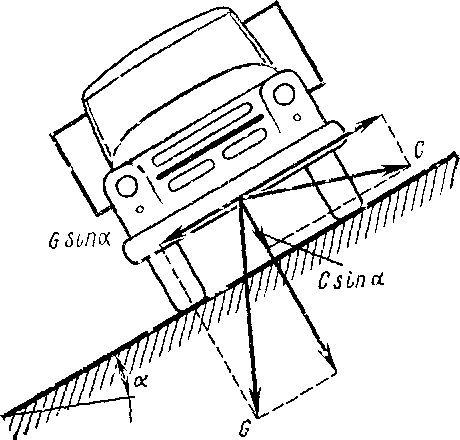
Рис. 14 Силы, действующие на автомобиль, движущийся по кривой

 

На автомобиль в поперечной плоскости к направлению дви­жения действуют следующие силы: вес автомобиля G, направ­ленный вертикально, и центробежная сила С, направленная го­ризонтально. Центробежной силе, стремящейся сдвинуть или оп­рокинуть автомобиль во внешнюю сторону от центра кривой, противодействует сила трения (сцепление между покрытием до­роги и шиной автомобиля). Если центробежная сила меньше сил сцепления, то поперечного скольжения не будет и устойчивость обеспечивается.

Условие устойчивости автомобиля при прохождении его по кривой получим, проектируя все найденные силы на наклонную поверхность покрытия, разделяя силы на сдвигающие и препят­ствующие сдвигу. Для этого разложим вес автомобиля на две составляющие: перпендикулярную к поверхности проезжей части Gcosα и параллельную поверхности Gsinα. Последняя при двускатном профиле будет иметь разные направления: внутрь кривой при движении автомобиля по внутренней полосе проез­жей части и во внешнюю сторону кривой при движении автомо­биля по внешней полосе, т. е. сила будет иметь один из знаков - плюс или минус.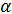

Разложим также и центробежную силу на перпендикуляр­ную к поверхности проезжей части С sinα и параллельную ей Ccosα.

Условие устойчивости автомобиля на кривой

 

Ccos G sin (G cos 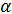+ Csi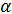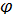n ) _n,

где 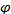_п - коэффициент поперечного сцепления, который по опыт­ным данным составляет часть от общего коэффициента; 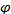_п = 0,3 .

 

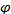Разделив обе части неравенства на cos α и выразив через по­перечный уклон i, после преобразований получим

 

C . ппппппппп

 

Последним членом С 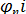ввиду его малости пренебрегаем. Тогда условие устойчивости автомобиля при прохождении его по кривой с учетом двускатного поперечного профиля примет вид

 

(). (11)

 

Пользуясь данным выражением, легко получить расчетные формулы для определения минимального радиуса кривой, попе­речного уклона проезжей части или допустимой скорости движе­ния автомобиля на кривой.

Подставляя в полученное выражение значение центробежной силы С получим

ппппппп

Отсюда

R 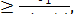(12)

 

где R— радиус кривой в плане, м; — скорость движения ав­томобиля м/с; g— ускорение свободного падения, м/с²; i— поперечный уклон проезжей части.

 

Знак плюс перед поперечным уклоном принимается при прохождении ав­томобиля по внутренней полосе проезжей части, минус — при прохождении его по внешней полосе. В первом случае попереч­ный уклон противодействует центробежной силе, во втором спо­собствует скольжению или опрокидыванию автомобиля во внеш­нюю сторону кривой.

Заменяя в формуле (12) размерность 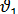(м\с) на 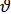(км\ч), получим

 

. (13)

 

Пользуясь полученной формулой, можно просле ­ дить, как изменяется ра ­ диус кривой, обеспечива ­ ющий безопасное движе­ние автомобиля с расчетной скоростью в зависи­мости от того, по какой полосе двускатной проез­жей части перемещайся автомобиль. Обычно в до­рожных расчетах прини­мают продольный коэф­фициент сцепления =0,2, соответствующий неблагоприятным усло­виям, мокрому и грязно­му покрытию.

 

Пример Если принять расчетную скорость движения автомобиля равной 100 км/ч (дорога III технической кате­гории) и поперечный уклон проезжей части i= 0,02, то на­именьший радиус кривой при движении автомобиля по внешней полосе движения: 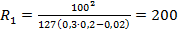; То же, по внутренней полосе: ппппппп

Очевидно, в этих условиях расчетный радиус кривой при­нимается равным 2000 м.

 

При особо неблагопри­ятных условиях, т. е. при гололеде, когда

φ=0,1, разница в радиусах для рассмотренных двух слу­чаев будет еще большей. Очевидно и водителям, и работникам дорожной службы необходимо при­нимать меры по обеспече­нию безопасности движе­ния, водители должны снижать скорость движения автомобилей, а работники дорожной службы повышать ше­роховатость поверхности дорожной одежды.

Решая основное выражение (13) относительно скорости, по­лучим формулу, по которой можно определить наибольшую ско­рость движения автомобиля на кривой определенного радиуса

 

мммммм 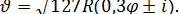(14)

 

Пример При R= 1000 м, i=0,03 и φ 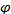=0,2 наибольшая скорость дви­жения автомобиля по внешней полосе движения ограничивается

мммммммммммммммм

На этом участке дороги работники дорожной службы должны установить знак ограничения скорости движения.

 

Лекция 8

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: