Алгоритм обработки результатов прямых измерений с многократными независимыми наблюдениями

Измерение состоит в получении информации о числовом значении измеряемой величины на основе сравнения известной величины (единица физической величины) и исследуемой величины. При этом узнают во сколько раз значение измеряемой величины больше или меньше единицы измерения. Например, при измерении длины объекта путем сравнения определили, что один метр меньше измеряемой величины в 5 раз, т.е. l = 5:1 (м); при измерении массы некоторого объекта определили, что один килограмм больше неизвестной величины в 4 раза, т.е. m=1:4 (кг). Таким образом вместо качественной характеристики величины (больше – меньше, легче – тяжелее, длиннее – короче и т.д.) получаем ее количественное значение.

Необходимость измерения обусловлена дефицитом информации о количественной характеристике измеряемой величины.

Подавляющее большинство измерений являются однократными. В обычных условиях (в быту, в торговле, во многих областях производственной деятельности) их точность вполне приемлема, а простота, высокая производительность (количество измерений в единицу времени) и низкая стоимость (по оценке трудозатрат) ставят их вне конкуренции. Многие люди до конца своей жизни остаются знакомыми только с однократными измерениями.

Многократное измерение одной и той же величины постоянного размера производится при повышенных требованиях к точности измерений. Такие измерения характерны при тонких научных экспериментах, высоких технологиях, в оборонной промышленности, для профессиональной метрологической деятельности и т.д. Это сложные, трудоемкие и дорогостоящие измерения, целесообразность которых должна быть всегда убедительно обоснована.

К многократным относятся измерения одного и того же размера физической величины, следующие друг за другом. Они могут быть обработаны в соответствии с требованиями математической статистики, согласно которой число отдельных измерений должно быть не менее четырех, входящих в ряд. Применение такого вида измерений дает возможность уменьшить влияние случайных погрешностей. Результат каждого наблюдения при этом дает оценку измеряемой величины.

Многократному измерению предшествует анализ априорной информации (информация, которой располагают до измерения) и тщательная подготовка к измерительному эксперименту.

Порядок выполнения многократных измерений рассмотрим на примере измерений с равноточными значениями отсчета. Если изменением измеряемой величины по времени можно пренебречь, то все значения отсчета проще всего получить путем многократного повторения операции сравнения с помощью одного и того же средства измерений. Отсчет в этом случае будет описываться эмпирической плотностью распределения вероятности р (х₁, х₂,…, х_i,…, x_n), где согласно основному постулату метрологии каждое значение отсчета является случайным числом, подчиняющимся этому закону распределения вероятности.

Такие значения отсчета х_i, имеющие одинаковую дисперсию, называются равноточными.

В процессе многократного прямого измерения получают n результатов наблюдений. При этом необходимо установить, подчиняются ли результаты наблюдений нормальному закону распределения. Применение этого закона объясняется тем, что рассеивание получаемых результатов вызывается множеством случайных факторов.

Для обработки полученных данных в целях определения значения исследуемой величины применяют стандартный метод (ГОСТ 8.207-76) с использованием следующего алгоритма (рис. 1.).

 

 

п/п	Действия по алгоритму
	Получение n результатов наблюдений (х1,х2,…хi,…xn)
	Исправление результатов наблюдений исключением (по возможности) система - тической погрешности ()
3	Вычисление среднего арифметического исправленных результатов наблюдений, принимаемых за результат измерения ()
4	Оценка среднего квадратического отклонения результата измерения (G)
	Исключение промахов (грубых погрешностей)
6	Принятия значения доверительной ве - роятности Р=0,95
	Определение коэффициента Стьюдента в зависимости от Р и n (tp,n)
	Оценка доверительных границ случайной составляющей погрешности результата измерения (оценка точности)
	Оценка неисключенной систематической составляющей погрешности (неисключен- ных остатков систематической погреш- ности) результатов измерения
	Оценка погрешности результата измерения ()
	Запись результата измерения с использованием правил округления

 

Рис. 1. Алгоритм обработки результатов многократных измерений

 

1. Наблюдения будем считать независимыми в том случае, если вероятность того или иного исхода каждого наблюдения не зависит от того, какие исходы имели другие опыты. Количество выполняемых наблюдений зависит от возможности проведения не одного, а ряда наблюдений, от требований к точности результата измерения.

2. Систематической () называют составляющую погрешности измерений, остающуюся постоянной или закономерно изменяющуюся при повторных измерениях одной и той же величины. Результаты наблюдений, полученные при наличии систематической погрешности, называют неисправленными. Постоянная систематическая погрешность не устраняется при многократных наблюдениях. Постоянная систематическая погрешность не искажает ни показателей точности измерений, ни результат нахождения переменной составляющей систематической погрешности. Постоянные () могут быть обнаружены лишь путем сравнения результатов измерений с другими, полученными с помощью более высокоточных методов и средств (например, с эталонами). Если известно, что все результаты наблюдений имеют одинаковую систематическую погрешность, ее исключают из результата измерений.

Наличие существенной переменной систематической погрешности искажает оценки характеристик случайной погрешности и аппроксимацию ее распределения. Поэтому она должна обязательно выявляться и исключаться из результатов измерений.

Систематическая погрешность может возникнуть на любом этапе измерительного эксперимента. Опасность представляет именно не выявленная систематическая погрешность. Все источники возникновения систематических погрешностей перечислить невозможно, но не существует также и универсальных методов их выявления и оценки. Известен ряд способов исключения систематической погрешности, которые условно можно разделить на четыре основные группы:

- устранение источников погрешностей до начала измерений (самый рациональный способ);

- исключение погрешностей в процессе измерения способами замещения, компенсацией погрешностей по знаку, противопоставления, симметричных наблюдений;

- внесение известных поправок в результат измерения (исключение погрешностей вычислением);

- оценка границ систематических погрешностей, если их нельзя исключить.

Неизвестность значений неисключенных остатков систематических погрешностей приводит к тому, что их вынуждены оценивать как случайные, что дает возможность определять доверительную погрешность в общем виде не конкретного средства измерений или объекта контроля, а любого из их совокупности. Это очень важно при разработке технической документации (методик выполнения измерений), а также и при проведении метрологической экспертизы.

Если известны границы систематической погрешности и нет оснований для того, чтобы приписать ей тот или иной закон распределения, принимается равномерное распределение.

Результат наблюдений, в который введены поправки с целью устранения систематических погрешностей, считается исправленным. Поправкой называют значение величины, одноименной с измеряемой, которые прибавляют или вычитают к полученному при измерении значению полученной величины с целью исключения систематической погрешности.

Если многократное измерение выполняется одним средством измерений, то поправки могут отличаться друг от друга из-за изменения во времени влияющих факторов. Если же используются одновременно несколько средств измерений, то поправки отличаются из-за индивидуальных особенностей каждого из них.

3. За результат измерения принимается среднее арифметическое значение результатов наблюдений, которое вычисляется по формуле:

, (6)

где: n – число наблюдений, x_i – результат i-го наблюдения в ряду наблюдений.

Среднее арифметическое при любом законе распределения вероятности результата измерения, является не только состоятельной, но и несмещенной оценкой среднего значения.

Точность результата многократного измерения зависит от эффективности оценки среднего значения. Чем она эффективнее (чем меньше ее рассеяние), тем выше точность. Для оценки эффективности служат различные критерии.

Вычисленные средние арифметические значения неисправленных результатов наблюдений и отклонений от них результатов наблюдений будут также неисправленными. Среднее арифметическое результатов наблюдений, в которые предварительно введены поправки для исключения систематических погрешностей, принимают за результат измерений.

Следует заметить, что введением поправки устраняют влияние только одной определенной систематической погрешности, а поэтому в результаты измерений приходится иногда вводить большое число поправок. Ограниченная точность определения поправок приводит к накоплению случайных погрешностей, в результате чего дисперсия результата измерения увеличивается. Поэтому экспериментатор должен определить оптимальную границу значений поправок, которые следует вводить в результаты наблюдений для получения более достоверных сведений о действительном (истинном) значении измеряемой величины.

При достаточном большом числе наблюдений среднее арифметическое стремится к действительному (истинному) значению измеряемой величины: _{действит.} при n . Среднее арифметическое обладает самым близким значением к действительному (истинному) значению измеряемой величины в отличие от результатов наблюдений, получаемых при многократном измерении.

4. После проведения серии измерений конкретной физической величины должно быть получено число, определяющее ее значение, и указана степень его достоверности, т.е. должен быть получен результат измерения. Но в данной серии из n измерений среднее арифметическое () является линейной функцией результатов отдельных наблюдений х₁,х₂,…х_i,…x_n и, если произвести новую серию из n измерений, то вследствие влияния отдельных факторов значения второй серии измерений будут отличаться от полученных в первой серии, а следовательно и новое значение будет иным.

Следовательно , полученное в одной из серии измерений, является случайным приближением к действительному (истинному) значению (). Чтобы иметь представление о возможных отклонениях среднего арифметического каждой серии измерений от , необходимо определить среднее отклонение значений средних арифметических каждого ряда измерений от . Например, при проведении трех серий измерений исследуемой величины получаем три ряда данных (m=3, m - число рядов), соответственно будем иметь три значения среднего арифметического ( _{1, 2, 3} ) по каждому ряду. Для определения среднего отклонения полученных от необходимо провести следующий расчет:

(7)

где m – число рядов измерений; j – номер ряда.

Простое усреднение значения ( - ), приведет к получению нуля (среднее значение случайной величины находится как раз посередине между отклонениями в ту или иную сторону), поэтому в качестве отклонения целесообразно взять квадрат указанной разницы ( - )². При усреднении получится величина большая нуля, и она уже может характеризовать меру отклонения случайной величины от .

Прежде, чем установить среднее отклонение от , рассмотрим отдельную серию измерений. Изложенное выше имеет место и в отношении отдельной серии измерений, т.е. нам необходимо рассчитать приближенное значение среднего квадратического отклонения среднего арифметического от каждого результата наблюдения в ряду – S (стандартное отклонение). При обработке результатов ограниченного числа наблюдений получаем:

, откуда . (8, 9)

Производя оценку действительного (истинного) значения измеряемой величины по результатам наблюдений, мы пользуемся методами теории вероятностей, применяемыми для оценки неизвестных параметров функции распределения случайной величины. Не вдаваясь в подробности теории вероятности, отметим, что появление в знаменателе выражения n-1 вместо n связано с заменой математического ожидания () средним арифметическим () незначительного числа наблюдений и введением в расчеты поправки , используемой при определении несмещенности оценки измеряемой величины.

Среднее арифметическое отличается от математического ожидания (действительного)/истинного значения) на величину случайной погрешности (погрешности среднего значения), которая подчиняется тому же закону распределения, что и погрешности результатов отдельных наблюдений, т.е. S – стандартное отклонение характеризует случайную погрешность каждого результата наблюдения.

Как упоминалось ранее, за результат измерения принимается среднее арифметическое значений результатов в ряду наблюдений. Оценка среднего квадратического отклонения результата измерения от действительного (истинного) значения осуществляется по формуле:

(10)

- характеризует погрешность окончательного результата измерения, т.е. дает представление о возможных отклонениях среднего арифметического от действительного (истинного) значения, а значит характеризует погрешность метода измерений.

5. Если есть подозрение о наличии грубых погрешностей, то их исключают из результатов наблюдений.

Грубая погрешность (промах) – это случайная погрешность результата отдельного наблюдения, входящего в ряд наблюдения, которая для данных условий резко отличается от остальных результатов этого ряда. Если промахи обнаруживаются в процессе измерений, то результаты, их содержащие, отбрасывают. Но необдуманное отбрасывание резко отличающихся от других результатов наблюдений при многократном измерении может привести к существенному искажению характеристик наблюдений. Однако чаще всего грубые погрешности выявляют только при окончательной обработке результатов наблюдений, при этом иногда учесть все обстоятельства, при которых они были получены, не представляется возможным. В таком случае при оценке грубых погрешностей прибегают к обычным методам проверки статистических гипотез (методы математической статистики).

Проверяемая гипотеза состоит в утверждении, что результат измерений Х_i не содержит грубой погрешности, а является одним из значений случайной величины. Обычно проверяют наибольшее Х_max и наименьшее Х_min значения результатов наблюдений.

Для проверки гипотез используют ряд критериев, предварительно определив, какому виду распределения соответствует результат наблюдения.

В зависимости от количества результатов наблюдений можно применять, например, следующие критерии, позволяющие обнаружит наличие промахов:

-при n 10 может быть использован критерий Шовенэ (Шовине);

-при 10 < n < 20 – критерий Романовского (критерий Греббса/Смирнова), критерий Диксона;

-при n 20…50: критерий Шарлье, критерий Райта (критерий трех сигм 3 –три стандартных отклонения 3S; различия заключаются только в символике, присваиваемой стандартному отклонению в различных источниках).

1,6S при n=3; 1,7S при n=6; 1,9S при n=8; 2,0S при n=10,

При использовании критерия Шовенэ промахом считается результат Х_i, если разность превышает значения S, определяемые в зависимости от числа измерений:

 

 

 

где S – стандартное отклонение, рассчитанное по формуле:

. (11)

Критерий Диксона (К_Д) – удобный и достаточно мощный критерий. При использовании этого критерия выполняют следующий порядок действий:

-результаты наблюдений располагают в вариационный возрастающий ряд х₁<х₂<…<x_n;

-определяют К_Д по формуле

(12)

-сравнивают значение К_Д и Z_дикс(q, n): если К_Д > Z_дикс(q, n), то результат отбрасывают как содержащий грубую погрешность; если К_Д < Z_дикс(q, n), то результат не содержит промаха с вероятностью Р=1-q.

Z_дикс(q, n) – критическая область критерия Диксона (приложение 3, табл.2).

Р (К_Д > Z_дикс(q, n))=q, (13)

где q – уровень значимости.

Уровень значимости – вероятность того, что появление сомнительного результата практически невозможно. Обычно q выбирается из ряда: 0,10;0,05;0,01 и т.д. Уровень значимости q=0,01 называют однопроцентным; q=0,02 – двухпроцентным и т.д.

Для данного q определяют критическую область значений критерия проверки нулевой гипотезы. Если значение критерия попадает в эту область, то гипотеза отвергается. Нулевая гипотеза заключается в утверждении, что «сомнительный» результат в действительности принадлежит к возможной совокупности полученных в заданных условиях результатов наблюдений, и получение такого результата вероятно.

Можно использовать также критерий Романовского:

; (14)

Вычисленное значение сравнивается с теоретическим значением 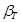, при выбираемом уровне значимости q (приложение 3, табл. 3). Напомним, что уровень значимости – это вероятность отвергнуть верную гипотезу при статистической проверке гипотезы. Если 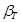, то результат Х_i считается промахом и отбрасывается.

Критерий 3 (или 3S) – наиболее распространенный. При этом считается, что результат, полученный с вероятность Р=0,003, маловероятен и его можно квалифицировать как промах, т.е. сомнительный результат Х_i должен быть исключен из результатов наблюдений, если > 3 (или > 3S).

6. Обычно при технических измерениях значения доверительной вероятности принимают равным Р=0,95. Если речь идет о безопасности, научных исследованиях, то доверительная вероятность принимается равной 0,99 и даже 0,999.

 

Доверительные вероятности, а также доверительные интервалы используются с целью увеличения достоверности замены действительного (истинного) значения измеряемой величины средним арифметическим значением. Доверительная вероятность Р (Р=1-q, где q – уровень значимости) есть вероятность того, что доверительный интервал со случайными границами «накроет» действительное (истинное) значение измеряемой величины.

Большая доверительная вероятность получается при большом доверительном интервале, поэтому, как показывает опыт, доверительная вероятность, равная 0,95 и даже 0,90, вполне достаточна для практических целей.

7. Вероятность того, что результаты измерения не выйдут за границы какого-либо интервала погрешности, определяется по площади, ограниченной кривой распределения и границами этого интервала, отложенными по оси абсцисс. Такой интервал (рис. 2) называют доверительным, а соответствующую ему вероятность появления случайной погрешности (заштрихованная площадь) P(t) – доверительной вероятностью.

0

 

Рис. 2. Доверительный интервал

Нижнюю и верхнюю границы доверительного интервала называют доверительными границами (- ; + ).

При определении доверительных границ случайной составляющей погрешности результата измерения проверяется гипотеза о том, что результаты наблюдений принадлежат нормальному распределению. Если это условие не выполняется, то методы вычисления доверительного интервала случайной погрешности должны быть указаны в методике выполнения конкретных измерений.

При n 15 гипотеза о нормальности распределения не проверяется.

Если 15<n<50, то используют составной критерий (ГОСТ 8.207-76). При числе результатов наблюдений n>50 для проверки гипотезы используют критерий 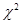(«хи-квадрат» или критерий Пирсона) или (Мизеса-Смирнова).

Точность измерений характеризуется средним квадратическим отклонением S случайных погрешностей, поэтому задача сводится к отыскиванию доверительного интервала , показывающего S c заданной доверительной вероятностью (надежностью) Р.

Если заранее известно, что результаты наблюдений подлежат нормальному распределению, доверительные границы (без учета знака) случайной погрешности результата измерения находят по формуле:

, (15)

где: t_s – коэффициент Стьюдента, который в зависимости от доверительной вероятности Р и числа результатов наблюдений n находят по таблице (см. приложение 3, табл. 1).

8. Неиключенная систематическая погрешность (НСП) результата образуется из неисключенных систематических погрешностей метода, средств измерений, погрешностей поправок и др.

При суммировании эти составляющие рассматриваются как случайные величины. При отсутствии данных о виде распределения неисключенных составляющих систематических погрешностей их распределения принимают за равномерные. Доверительную вероятность для вычисления границ НСП принимают той же, что при вычислении границ случайной погрешности результата измерения.

В случае равномерного распределения НСП доверительные границы (без учета знака) вычисляют по формуле:

(16)

где - граница i-ой НСП; К- коэффициент, определяемый принятой Р- доверительной вероятностью; m – число суммируемых НСП. При Р=0,95 К=1,1.

9. Если , то НСП пренебрегают и в качестве границы погрешности результата измерения принимают .

Если 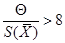, то пренебрегают случайной погрешностью и считают, что .

Если 0,8< 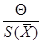<8, то при определении погрешности необходимо учитывать и случайную и систематическую.

10. Результат измерения представляют в виде и погрешности .

Для случая симметричных доверительных границ .

При исключенных систематических погрешностях результат измерения запишется как или .

11. Точность измерения равна разности между средним выборочным значением и средним генеральной совокупности :

. (17)

Генеральной средней называют среднее арифметическое значение признака генеральной совокупности (совокупности объектов, из которых производится выборка). Выборочной средней называют среднее арифметическое значение признака выборочной совокупности (совокупности случайно отобранных объектов из генеральной совокупности).

Чтобы установить адекватность описания выборочной совокупностью поведения генеральной совокупности, необходимо проверить гипотезу о том, значимо ли отличаются между собой 2 средних значения ( и ). Если сравнивать с (при нормальном распределении), то по формуле:

(18)

вычисляют критерий t. Вычисленную величину t сравнивают со значением t_s, найденным в таблице коэффициентов Стьюдента, для выбранной доверительной вероятности и числа степеней свободы f=n-1. Если t > t_s, то различие между и является значимым, т.е. выборочная совокупность неадекватно описывает поведение генеральной совокупности, исходя из чего необходимо изменять объем выборочной совокупности (выборки).

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: