 |
Обработка результатов экспертизы
|
|
|
|
Основным результатом обработки результатов экспертизы является вектор весов факторов:
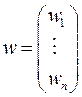
который строится в два этапа.
1)Построение системы векторов или матрицы Х = (хij)
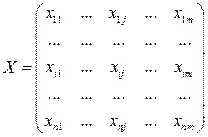
Это матрица индивидуальных весов, где j-й столбец описывает веса, приписанные j-м экспертом j=1...m,повсем n факторам, причем
для j=1,…m
2)Построение групповых весов (при использовании метода ранжирования обычно получают также групповые ранги).
Если мнения экспертов представлены в виде матриц парных сравнений, матрица нормированных весов Х на базе последовательности матриц В: { В',..., Вj,..., Вm }. Вначале определяется сумма в каждой строке матрицы В, дающая вектор-столбец β:
β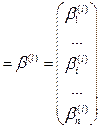 
где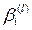 
— сумма элементов по i-й строке;
= 
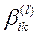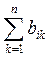(bik—элемент матрицы В = В j).
Затем осуществляется нормирование элементов вектора, приводящее к весам:
причем
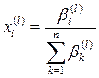
В случае, если используется метод ранжирования, матрица строится в два этапа:
1)Строится матрица преобразованных рангов
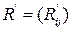
элементы которой Rij вычисляются по следующему правилу:
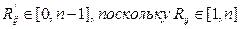
2)Строится матрица нормированных весов Х= (хij), где
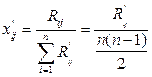
поскольку
для j=1,2,…m
1.2.4 Построение центроида
Центроид (групповое мнение) находится где-то внутри области, ограниченной крайними мнениями», а фактическое его местонахождение зависит от выбора меры или критерия расстояния между векторами х 1... х m.
Классической мерой близости является квадрат отклонения. Поэтому наиболее распространенный метод построения центроида есть нахождение вектора-столбца w, такого, что
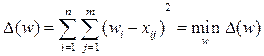
Известно, что это выполняется тогда и только тогда, когда
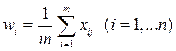
т. е.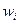 
является средним арифметическим оценок варианта ai экспертами Э1,..., Эj,..., Эm.
|
|
|
При использовании метода ранжирования в качестве результата часто приводят групповые ранги.
Анализ результатов
На этапе анализа пытаются оценить, можно ли доверять полученным результатам. А именно, насколько плотно расположенными друг к другу оказались мнения экспертов.
Традиционной мерой оценки плотности области мнений для случая голосования методом ранжирования является коэффициент конкордации Кендалла(W ).
Коэффициент конкордации W изменяется от 1 до приблизительно нуля, при этом он равен 1, если все ранжировки комонотонны, т. е. совпадают, и наоборот, равен нулю, если они образуют все возможные перестановки, т. е. они все контрамонотонны (это в точности возможно только при п=т).
Строится W следующим образом.
Вначале в каждой строке матрицы рангов R={Rj) вычисляется сумма элементов (рангов):
По матрице R в целом вычисляется среднее значение R;.
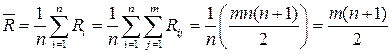
Далее определяется сумма s квадратов отклонений значений в строке матрицы R от 
Коэффициент конкордации W вычисляется на основе выражения:
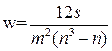
Для случая наличия связанных рангов W приобретает более сложный вид, поэтому данное выражение дает только приближенное значение.
Содержание работы
Вариант работы определяется порядковым номером в списке группы.
Работа выполняется с помощью табличного редактора Microsoft Excel.
Парные оценки
Для данных экспертизы, представленных в виде матриц парных оценок, требуется:
1) построить групповое мнение (центроид);
2) определить коэффициент конкордации.
Перечень вариантов приведен в разделе 1.6.1.
Ранжирование
Для данных экспертизы, представленных в виде матрицы рангов, требуется:
1) построить групповое мнение (центроид);
2) определить коэффициент конкордации.
Перечень вариантов приведен в разделе 1.6.2.
Отчет по работе
Отчет по работе должен включать исходные данные и результаты.
|
|
|
1) Расчеты и результаты для заданий по пп. 1.3.1, 1.3.2 должны быть размещены на отдельных листах с именами 1 и 2 соответственно.
2) Исходные, промежуточные и итоговые данные для экспертов (п. 1.3.1) должны располагаться по левой стороне листа друг под другом в соответствии со структурой:
А - матрица парных сравнений
Б - матрица сумм элементов строк
В - вектор-столбец нормированных весов
Г - вектор-столбцов рангов
å - контрольная сумма элементов столбца.
3) Результаты помещаются в нижней части листа также по левой стороне.
Групповое мнение:
А - матрица весов,
Б - вектор-столбец группового мнения (веса),
В - вектор-столбец группового мнения (ранги),
å - контрольная сумма элементов столбца.
Коэффициент конкордации:
А - матрица рангов,
Б - суммы элементов строк А,
В – сумма квадратов разностей элементов Б и среднего по матрице А,
Г – коэффициент конкордации,
å - контрольная сумма элементов столбца.
Точность вычислений и результата – два десятичных знака.
1.5 Контрольные вопросы
1) Что такое экспертиза?
2) Из каких основных шагов состоит процесс проведения экспертного оценивания?
3) Экспертное оценивание относится к качественным или количественным методам оценивания?
4) Какие методы сбора данных экспертизы являются наиболее употребительными?
5) Какие сложности могут возникать при использовании сбора данных на основе метода парных оценок?
6) Каким образом определяется групповое мнение на основании собранных данных экспертизы?
7) Как определяется и как рассчитывается коэффициент конкордации?
Варианты
Метод парных сравнений
Номера матриц с результатами экспертизы
| № | Номера матриц | ||||
| Э1 | Э2 | Э3 | Э4 | Э5 | |
Матрицы с результатами экспертизы
|
|
|
Метод ранжирования
|
|
|
|
|
|
Результаты экспертизы (матрицы рангов)
| 1. | Э1 | Э2 | Э3 | Э4 | Э5 |
| Ф1 | 3,0 | 2,0 | 2,0 | 2,0 | 2,0 |
| Ф2 | 1,0 | 1,0 | 1,0 | 1,0 | 4,0 |
| Ф3 | 6,0 | 4,0 | 4,5 | 4,0 | 3,0 |
| Ф4 | 5,0 | 5,0 | 3,0 | 6,0 | 6,0 |
| Ф5 | 3,0 | 3,0 | 4,5 | 3,0 | 1,0 |
| Ф6 | 3,0 | 6,0 | 6,0 | 5,0 | 5,0 |
| 2. | Э1 | Э2 | Э3 | Э4 | Э5 |
| Ф1 | 2,0 | 3,0 | 2,0 | 2,0 | 2,0 |
| Ф2 | 3,0 | 1,0 | 1,0 | 1,0 | 1,0 |
| Ф3 | 1,0 | 6,0 | 4,0 | 4,5 | 4,5 |
| Ф4 | 5,0 | 5,0 | 5,0 | 3,0 | 3,0 |
| Ф5 | 4,0 | 3,0 | 3,0 | 4,5 | 4,5 |
| Ф6 | 6,0 | 3,0 | 6,0 | 6,0 | 6,0 |
| 3. | Э1 | Э2 | Э3 | Э4 | Э5 |
| Ф1 | 2,0 | 3,0 | 3,0 | 2,0 | 2,0 |
| Ф2 | 3,0 | 2,0 | 1,0 | 1,0 | 1,0 |
| Ф3 | 1,0 | 4,0 | 6,0 | 4,0 | 4,0 |
| Ф4 | 5,0 | 6,0 | 5,0 | 5,0 | 5,0 |
| Ф5 | 4,0 | 1,0 | 3,0 | 3,0 | 3,0 |
| Ф6 | 6,0 | 5,0 | 3,0 | 6,0 | 6,0 |
| 4. | Э1 | Э2 | Э3 | Э4 | Э5 |
| Ф1 | 2,0 | 2,0 | 3,0 | 3,0 | 2,0 |
| Ф2 | 3,0 | 1,0 | 2,0 | 3,0 | 1,0 |
| Ф3 | 1,0 | 4,0 | 1,0 | 1,0 | 4,0 |
| Ф4 | 5,0 | 5,0 | 5,0 | 5,0 | 6,0 |
| Ф5 | 4,0 | 3,0 | 6,0 | 3,0 | 3,0 |
| Ф6 | 6,0 | 6,0 | 4,0 | 6,0 | 5,0 |
| 5. | Э1 | Э2 | Э3 | Э4 | Э5 |
| Ф1 | 3,0 | 3,0 | 4,0 | 2,0 | 3,0 |
| Ф2 | 2,0 | 3,0 | 3,0 | 4,0 | 2,0 |
| Ф3 | 1,0 | 1,0 | 1,0 | 3,0 | 1,0 |
| Ф4 | 5,0 | 5,0 | 5,0 | 6,0 | 6,0 |
| Ф5 | 6,0 | 3,0 | 2,0 | 1,0 | 5,0 |
| Ф6 | 4,0 | 6,0 | 6,0 | 5,0 | 4,0 |
| 6. | Э1 | Э2 | Э3 | Э4 | Э5 |
| Ф1 | 2,0 | 3,5 | 3,0 | 2,5 | 3,5 |
| Ф2 | 4,0 | 3,5 | 2,0 | 4,0 | 3,5 |
| Ф3 | 3,0 | 1,0 | 1,0 | 2,5 | 2,0 |
| Ф4 | 6,0 | 5,0 | 6,0 | 5,0 | 5,0 |
| Ф5 | 1,0 | 2,0 | 5,0 | 1,0 | 1,0 |
| Ф6 | 5,0 | 6,0 | 4,0 | 6,0 | 6,0 |
| 7. | Э1 | Э2 | Э3 | Э4 | Э5 |
| Ф1 | 3,5 | 2,0 | 2,5 | 3,0 | 2,0 |
| Ф2 | 3,5 | 4,0 | 4,0 | 4,0 | 3,0 |
| Ф3 | 2,0 | 1,0 | 2,5 | 2,0 | 4,0 |
| Ф4 | 5,0 | 6,0 | 5,0 | 6,0 | 6,0 |
| Ф5 | 1,0 | 3,0 | 1,0 | 1,0 | 1,0 |
| Ф6 | 6,0 | 5,0 | 6,0 | 5,0 | 5,0 |
| 8. | Э1 | Э2 | Э3 | Э4 | Э5 |
| Ф1 | 3,0 | 3,0 | 2,0 | 2,0 | 2,0 |
| Ф2 | 2,0 | 1,0 | 1,0 | 1,0 | 1,0 |
| Ф3 | 4,0 | 6,0 | 4,0 | 4,5 | 4,0 |
| Ф4 | 6,0 | 5,0 | 5,0 | 3,0 | 6,0 |
| Ф5 | 1,0 | 3,0 | 3,0 | 4,5 | 3,0 |
| Ф6 | 5,0 | 3,0 | 6,0 | 6,0 | 5,0 |
| 9. | Э1 | Э2 | Э3 | Э4 | Э5 |
| Ф1 | 2,0 | 3,0 | 2,0 | 3,0 | 2,0 |
| Ф2 | 1,0 | 2,0 | 3,0 | 1,0 | 1,0 |
| Ф3 | 4,0 | 6,0 | 4,0 | 5,0 | 4,5 |
| Ф4 | 5,0 | 5,0 | 6,0 | 6,0 | 3,0 |
| Ф5 | 3,0 | 1,0 | 1,0 | 3,0 | 4,5 |
| Ф6 | 6,0 | 4,0 | 5,0 | 3,0 | 6,0 |
| 10. | Э1 | Э2 | Э3 | Э4 | Э5 |
| Ф1 | 3,0 | 2,0 | 3,0 | 2,0 | |
| Ф2 | 3,0 | 3,0 | 3,0 | 3,0 | |
| Ф3 | 1,0 | 1,0 | 1,0 | 3,5 | 1,0 |
| Ф4 | 5,0 | 6,0 | 5,5 | 5,5 | |
| Ф5 | 3,0 | 4,0 | 5,5 | 3,5 | 5,5 |
| Ф6 | 6,0 | 5,0 | 3,0 | 4,0 | |
| 11. | Э1 | Э2 | Э3 | Э4 | Э5 |
| Ф1 | 2,0 | 3,0 | 2,0 | 3,0 | 2,0 |
| Ф2 | 1,0 | 3,0 | 3,0 | 2,0 | 3,0 |
| Ф3 | 4,0 | 1,0 | 1,0 | 1,0 | 1,0 |
| Ф4 | 5,0 | 5,0 | 6,0 | 5,5 | 5,5 |
| Ф5 | 3,0 | 3,0 | 4,0 | 5,5 | 5,5 |
| Ф6 | 6,0 | 6,0 | 5,0 | 4,0 | 4,0 |
| 12. | Э1 | Э2 | Э3 | Э4 | Э5 |
| Ф1 | 2,0 | 2,0 | 2,0 | 2,0 | 1,0 |
| Ф2 | 1,0 | 4,0 | 3,0 | 1,0 | 3,0 |
| Ф3 | 4,5 | 3,0 | 1,0 | 4,0 | 3,0 |
| Ф4 | 3,0 | 6,0 | 6,0 | 5,0 | 5,0 |
| Ф5 | 4,5 | 1,0 | 4,0 | 3,0 | 3,0 |
| Ф6 | 6,0 | 5,0 | 5,0 | 6,0 | 6,0 |
| 13. | Э1 | Э2 | Э3 | Э4 | Э5 |
| Ф1 | 2,0 | 3,0 | 1,0 | 2,0 | 3,0 |
| Ф2 | 1,0 | 2,0 | 3,0 | 3,0 | 2,0 |
| Ф3 | 4,5 | 1,0 | 3,0 | 1,0 | 1,0 |
| Ф4 | 3,0 | 6,0 | 5,0 | 5,5 | 5,0 |
| Ф5 | 4,5 | 5,0 | 3,0 | 5,5 | 6,0 |
| Ф6 | 6,0 | 4,0 | 6,0 | 4,0 | 4,0 |
| 14. | Э1 | Э2 | Э3 | Э4 | Э5 |
| Ф1 | 3,0 | 2,0 | 2,0 | 3,5 | 2,5 |
| Ф2 | 3,0 | 1,0 | 4,0 | 3,5 | 4,0 |
| Ф3 | 1,0 | 4,0 | 3,0 | 1,0 | 2,5 |
| Ф4 | 5,0 | 6,0 | 6,0 | 5,0 | 5,0 |
| Ф5 | 3,0 | 3,0 | 1,0 | 2,0 | 1,0 |
| Ф6 | 6,0 | 5,0 | 5,0 | 6,0 | 6,0 |
| 15. | Э1 | Э2 | Э3 | Э4 | Э5 |
| Ф1 | 4,0 | 2,0 | 3,5 | 3,0 | 2,0 |
| Ф2 | 3,0 | 4,0 | 3,5 | 2,0 | 4,0 |
| Ф3 | 1,0 | 3,0 | 1,0 | 1,0 | 1,0 |
| Ф4 | 5,0 | 6,0 | 5,0 | 6,0 | 6,0 |
| Ф5 | 2,0 | 1,0 | 2,0 | 5,0 | 3,0 |
| Ф6 | 6,0 | 5,0 | 6,0 | 4,0 | 5,0 |
| 16. | Э1 | Э2 | Э3 | Э4 | Э5 |
| Ф1 | 3,0 | 3,0 | 2,0 | 2,0 | 1,0 |
| Ф2 | 2,0 | 4,0 | 3,0 | 1,0 | 3,0 |
| Ф3 | 1,0 | 2,0 | 1,0 | 3,5 | 3,0 |
| Ф4 | 6,0 | 6,0 | 6,0 | 5,0 | 5,0 |
| Ф5 | 5,0 | 1,0 | 4,0 | 3,5 | 3,0 |
| Ф6 | 4,0 | 5,0 | 5,0 | 6,0 | 6,0 |
| 17. | Э1 | Э2 | Э3 | Э4 | Э5 |
| Ф1 | 3,0 | 3,5 | 2,0 | 3,0 | 3,0 |
| Ф2 | 2,0 | 3,5 | 1,0 | 2,0 | 2,0 |
| Ф3 | 1,0 | 1,0 | 4,5 | 1,0 | 1,0 |
| Ф4 | 5,0 | 5,0 | 3,0 | 4,5 | 6,0 |
| Ф5 | 6,0 | 2,0 | 4,5 | 4,5 | 5,0 |
| Ф6 | 4,0 | 6,0 | 6,0 | 6,0 | 4,0 |
| 18. | Э1 | Э2 | Э3 | Э4 | Э5 |
| Ф1 | 2,0 | 2,5 | 3,5 | 2,0 | 3,0 |
| Ф2 | 3,0 | 4,0 | 3,5 | 4,0 | 2,0 |
| Ф3 | 4,0 | 2,5 | 2,0 | 1,0 | 6,0 |
| Ф4 | 6,0 | 5,0 | 5,0 | 6,0 | 5,0 |
| Ф5 | 1,0 | 1,0 | 1,0 | 3,0 | 1,0 |
| Ф6 | 5,0 | 6,0 | 6,0 | 5,0 | 4,0 |
| 19. | Э1 | Э2 | Э3 | Э4 | Э5 |
| Ф1 | 2,0 | 2,0 | 2,5 | 3,5 | 3,0 |
| Ф2 | 3,0 | 4,0 | 4,0 | 3,5 | 2,0 |
| Ф3 | 1,0 | 3,0 | 2,5 | 2,0 | 6,0 |
| Ф4 | 5,0 | 6,0 | 5,0 | 5,0 | 5,0 |
| Ф5 | 4,0 | 1,0 | 1,0 | 1,0 | 1,0 |
| Ф6 | 6,0 | 5,0 | 6,0 | 6,0 | 4,0 |
| 20. | Э1 | Э2 | Э3 | Э4 | Э5 |
| Ф1 | 3,0 | 4,0 | 3,5 | 2,5 | 2,0 |
| Ф2 | 2,0 | 3,0 | 3,5 | 4,0 | 4,0 |
| Ф3 | 1,0 | 1,0 | 1,0 | 2,5 | 1,0 |
| Ф4 | 5,0 | 5,0 | 5,0 | 5,0 | 6,0 |
| Ф5 | 6,0 | 2,0 | 2,0 | 1,0 | 3,0 |
| Ф6 | 4,0 | 6,0 | 6,0 | 6,0 | 5,0 |
| 21. | Э1 | Э2 | Э3 | Э4 | Э5 |
| Ф1 | 2,0 | 4,0 | 3,5 | 2,0 | 2,5 |
| Ф2 | 1,0 | 3,0 | 3,5 | 4,0 | 4,0 |
| Ф3 | 4,0 | 1,0 | 2,0 | 1,0 | 2,5 |
| Ф4 | 6,0 | 5,0 | 5,0 | 6,0 | 5,0 |
| Ф5 | 3,0 | 2,0 | 1,0 | 3,0 | 1,0 |
| Ф6 | 5,0 | 6,0 | 6,0 | 5,0 | 6,0 |
| 22. | Э1 | Э2 | Э3 | Э4 | Э5 |
| Ф1 | 2,0 | 3,0 | 3,0 | 2,0 | 2,0 |
| Ф2 | 4,0 | 4,0 | 1,0 | 3,0 | 1,0 |
| Ф3 | 1,0 | 2,0 | 5,0 | 1,0 | 3,5 |
| Ф4 | 6,0 | 6,0 | 6,0 | 6,0 | 5,0 |
| Ф5 | 3,0 | 1,0 | 3,0 | 4,0 | 3,5 |
| Ф6 | 5,0 | 5,0 | 3,0 | 5,0 | 6,0 |
| 23. | Э1 | Э2 | Э3 | Э4 | Э5 |
| Ф1 | 2,5 | 3,0 | 2,0 | 3,0 | 3,0 |
| Ф2 | 4,0 | 2,0 | 3,0 | 3,0 | 2,0 |
| Ф3 | 2,5 | 6,0 | 4,0 | 1,0 | 1,0 |
| Ф4 | 5,0 | 5,0 | 6,0 | 5,5 | 5,5 |
| Ф5 | 1,0 | 1,0 | 1,0 | 5,5 | 5,5 |
| Ф6 | 6,0 | 4,0 | 5,0 | 3,0 | 4,0 |
| 24. | Э1 | Э2 | Э3 | Э4 | Э5 |
| Ф1 | 2,0 | 3,0 | 3,0 | 2,0 | 2,0 |
| Ф2 | 3,0 | 2,0 | 3,0 | 1,0 | 4,0 |
| Ф3 | 1,0 | 4,0 | 1,0 | 4,0 | 3,0 |
| Ф4 | 5,0 | 6,0 | 5,0 | 6,0 | 6,0 |
| Ф5 | 4,0 | 1,0 | 3,0 | 3,0 | 1,0 |
| Ф6 | 6,0 | 5,0 | 6,0 | 5,0 | 5,0 |
Метод анализа иерархий
Цель работы
Практическое изучение метода анализа иерархий
Теоретические сведения
Метод анализа иерархий, разработанный и опубликованный в 1970 году американским математиком Саати [3], относится к классу критериальных. Он получил очень широкое распространение и в настоящее время продолжает активно применяться - см., например, [6] (задача составления оптимального производственного плана нефтепереработки), [7] (задача оценки недвижимости).
На первом этапе применения метода предусматривается структурирование проблемы в виде иерархии или сети. Иерархия строится с вершины (целей — с точки зрения управления), через промежуточные уровни (критерии, от которых зависят последующие уровни) к самому низкому уровню (который обычно является перечнем вариантов выбора).
Иерархия считается полной, если каждый элемент заданного уровня функционирует как критерий для всех элементов нижестоящего уровня. В противном случае иерархия — неполная. Нетрудно понять процесс определения весов в случае неполной иерархии, так как используются приоритеты соответствующего элемента, по отношению к которому производится оценка, т. е. иерархия может быть разделена на подиерархии, имеющие общим самый верхний элемент.
Для объяснения метода анализа иерархий рассмотрим пример, иллюстрирующий иерархическое представление задачи. Предположим, что перед нами стоит задача выбора автомобиля из совокупности, члены которой (модели автомобилей) обозначаются как А, Б, В и Г.
Определив на первом (высшем) уровне общую цель — «Автомобиль» - на втором уровне находятся пять факторов или критериев, уточняющих цель, и на третьем (нижнем) уровне находятся четыре автомобиля - кандидата, которые должны быть оценены по отношению к критериям второго уровня.
В качестве критериев, определяющих наш выбор, используются такие критерии:
1) Вместительность салона и багажника
2) Экономичность (расход горючего)
3) Ходовые качества
4) Дизайн
5) Стоимость
Следующим шагом метода после выполнения шага иерархического или сетевого воспроизведения проблемы производится установление приоритетов критериев и оценка каждого вариантов альтернативы по критериям. В методе анализа иерархий элементы задачи сравниваются попарно по отношению к их воздействию («весу», или «интенсивности») на общую для них характеристику. Проведем парные сравнения, приводящие к матричной форме. Сравнивая набор составляющих проблемы друг с другом, получаем следующую квадратную матрицу:
Очевидно, что эта матрица имеет свойства обратной симметричности, т. е.
где индексы i и j относятся к строке и столбцу соответственно.
Пусть А1, А2, Аз,..., Аn — множество из n элементов и w1, w2w3,..., wn — соответственно их веса, или интенсивности. С использованием метода анализа иерархий вес, или интенсивность, каждого элемента сравниваются с весом, или интенсивностью, любого другого элемента множества по отношению к общему для них свойству или цели. Сравнение весов можно представить квадратной таблицей, в которой числа могут быть расположены следующим образом
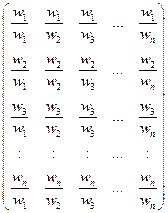
Если w1, w2, w3..., wn неизвестны заранее, то попарные сравнения элементов производятся с использованием субъективных суждений, оцениваемых численно по некоторой шкале, а вслед за чем решается проблема нахождения компонент w.
Для фиксации результата сравнения пары альтернатив может использоваться, в частности, шкала, предложенная автором метода:
1 - равноценность
3 - умеренное превосходство
5 - сильное превосходство
7 - очень сильное превосходство
9 - высшее (крайнее) превосходство
Значения 2,4,6,8 используются для обозначения промежуточной между перечисленными значениями степени превосходства.
Если элемент i важнее элемента j, то в клетку заносится положительное целое (от 1 до 9); в противном случае — обратное число (дробь). Относительная важность любого элемента, сравниваемого с самим собой, равна 1; поэтому диагональ матрицы (элементы от левого верхнего угла до нижнего правого) содержит только единицы. Симметричные клетки заполняются обратными в
|
|
|
