Уровень 2 - матрицы парных сравнений критериев

Кр1

Кр2

Кр3

Кр4

Кр5

Кр6

Кр1

1/2

Кр2

1/3

1/2

Кр3

1/4

1/2

1/2

1/2

Кр4

Кр5

1/5

1/3

1/3

Кр6

1/2

Кр1

Кр2

Кр3

Кр4

Кр5

Кр6

Кр1

1/2

Кр2

1/2

Кр3

Кр4

1/2

1/3

1/2

Кр5

1/3

1/2

1/2

1/2

Кр6

1/2

Кр1

Кр2

Кр3

Кр4

Кр5

Кр6

Кр1

1/2

Кр2

1/2

1/5

1/2

Кр3

1/5

1/2

1/9

1/3

Кр4

Кр5

Кр6

1/2

1/2

1/2

Кр1

Кр2

Кр3

Кр4

Кр5

Кр6

Кр1

1/4

1/2

Кр2

1/2

1/2

1/3

1/2

Кр3

1/3

1/2

1/7

1/5

1/2

Кр4

Кр5

1/2

Кр6

1/2

1/5

1/3

Кр1

Кр2

Кр3

Кр4

Кр5

Кр6

Кр1

1/2

1/5

Кр2

1/2

Кр3

1/3

1/5

1/2

1/9

Кр4

1/2

1/4

1/7

1/2

Кр5

Кр6

1/5

1/9

1/2

1/9

Кр1

Кр2

Кр3

Кр4

Кр5

Кр6

Кр1

1/2

1/5

Кр2

Кр3

1/3

1/6

1/7

Кр4

1/5

1/5

1/2

1/3

1/9

Кр5

1/3

1/2

1/3

Кр6

Кр1

Кр2

Кр3

Кр4

Кр5

Кр6

Кр1

1/2

1/5

Кр2

1/3

1/5

1/7

Кр3

1/3

Кр4

Кр5

1/2

1/2

1/5

1/7

Кр6

1/4

1/7

1/9

1/3

Кр1

Кр2

Кр3

Кр4

Кр5

Кр6

Кр1

1/3

1/5

Кр2

1/5

1/7

1/3

1/9

1/2

Кр3

1/2

Кр4

1/3

1/7

1/9

1/2

Кр5

Кр6

1/2

1/7

1/5

 

Уровень 3 - матрицы парных сравнений объектов

Вариант 1

	А	Б	В
А
Б	1/5
В	1/7	1/2
	А	Б	В
А			1/4
Б	1/4		1/7
В
	А	Б	В
А
Б	1/4
В	1/5	1/2
	А	Б	В
А			1/2
Б			1/2
В
	А	Б	В
А
Б	1/4		1/3
В	1/3
	А	Б	В
А
Б	1/4		1/2
В	1/2

 

 

Вариант 2

	А	Б	В
А		1/2
Б
В	1/3	1/3
	А	Б	В
А			1/5
Б			1/8
В
	А	Б	В
А		1/2	1/2
Б
В		1/2
	А	Б	В
А		1/2
Б
В		1/3
	А	Б	В
А
Б
В	1/2	1/3
	А	Б	В
А		1/2
Б
В	1/2	1/2

 

Вариант 3

	А	Б	В
А		1/2	1/3
Б			1/2
В
	А	Б	В
А			1/2
Б	1/2		1/2
В
	А	Б	В
А
Б	1/2
В	1/3	1/2
	А	Б	В
А			1/3
Б			1/2
В
	А	Б	В
А			1/2
Б	1/2		1/3
В
	А	Б	В
А		1/2	1/5
Б			1/5
В

Количественное оценивание сложных систем

Цель работы

Изучение:

1) использования частных и обобщенных показателей сложных систем;

2) критериев оценивания сложных систем;

3) выбора существенного множества альтернатив;

4) методов свертки частных показателей.

Теоретические сведения

Каждое i- ое качество j -ой системы, i= 1,..., п; j = 1,..., т, может быть описано с помощью некоторой переменной отображающей опре­де­ле­н­ное свойство системы, значение которой характеризует меру этого ка­чества. Эта мера на­зы­вается показателем свойства или час­т­ным по­казателем качества си­с­те­мы. Каждый показатель y_i может при­ни­мать зна­чения из множества (области) до­пустимых значений .

Обобщенным показателем качества j -ой системы называется век­тор , компонентами которого являются показатели отдельных си­с­темных свойств. Размерность этого вектора определяется числом сущест­­ве­н­­ных свойств системы (обратим внимание на то, что обобщенным по­ка­за­те­лем качества является именно вектор, а не про­стое множество ча­с­т­ных по­ка­зателей, поскольку ме­ж­ду отдель­ными свойствами могут су­ще­ст­во­вать свя­­зи, которые в рамках те­о­рии множеств описать весьма сложно).

Частные показатели имеют различную физическую природу и в соответствии с этим различную размерность. Поэтому при переходе к обобщенному по­ка­за­телю качества следует опери­ровать не с самими показателями, а с их нор­ми­рован­ными значениями, обеспечивающими приведение показателей к одному масштабу, что необходимо для их сопоставления.

Задача нормировки решается, как правило, введением отно­сительных без­раз­ме­рных показателей, представляющих собой отношение измеренного ча­с­т­ного показателя к некоторой нормирующей величине, измеряемой в тех же единицах, что и сам показатель

где - некоторое «идеальное» значение i -го показателя.

Выбор нормирующего делителя для перевода частных пока­зателей в безраз­ме­р­ную форму в значительной мере носит субъек­тивный характер и должен обосновываться в каждом конкрет­ном случае.

Возможны несколько подходов к выбору нормирующего де­лителя. Укажем следующие.

1) может задаваться ЛПР. Такой способ задания означает, что значе­ние сле­дует воспринимать как об­разцовое.

2) Можно положить .

3) В качестве может быть взята разность между максимальным и ми­­­ни­­мальным до­пустимыми значениями частного показателя.

Требуемое качество системы задается правилами (условиями), которым дол­ж­ны удовлетворять показатели существенных свойств, а проверка их выпол­не­ния называется оцениванием ка­чества системы. Таким образом, кри­те­рий ка­чества есть показа­тель существенных свойств системы и правило его оценивания.

Все критерии в общем случае могут принадлежать одному из трех классов.

Критерий пригодности

Согласно этому критерию j -ая система считается пригодной, если значения всех частных показателей этой системы принадлежат области допустимых значений частных показателей.

Критерий оптимальности

Согласно этому критерию j -ая система считается оптимальной по i-му по­ка­за­телю качества, если все зна­че­ния частных показателей качества при­на­д­ле­жат допустимой области и существует хотя бы один част­ный по­ка­за­тель ка­чества , по которому достигается оптимум.

Критерий превосходства

Согласно этому критерию j -ая система считается превосходной, если все зна­че­ния частных показателей качества принадлежат допустимой области и система оптимальна по всем показателям.

Иллюстрация приведенных формулировок приведена на Рис. 3‑1 где по свойствам у_х и у₂ сравниваются характеристики пяти систем { S¹, S², S³, S⁴, S⁵ },

Рис. 3‑1. Примеры критериев оценивания

 

имеющие допустимые области адекватности значений у₁ и у₂, для которых оп­тимальные значения определе­ны как и соответственно.

Из рисунка видно, что системы S¹, S², S³, S⁴ пригодны по показателям у₁ и у₂. Система S⁵ не является пригодной.

Системы S³, S⁴ оптимальны по показателю у₂.

Система S³ является превосходной.

Оцен­ка сложных систем в условиях определенности на основе мето­дов векторной оптимизации проводится в три этапа.

На первом этапе с использованием системного анализа опре­деляются част­ные показатели и критерии эффективности.

На вто­ром этапе находится множество Парето и формулируется задача мно­го­­кри­териальной оптимизации.

На третьем этапе задача решается путем скаляризации критериев с устра­не­­нием многокритериальности.

Множество Парето определяется как подмножество А* мно­жес­тва альтер­на­тив А. Множество А * (переговорное множество, множество ко­м­­п­­ро­­мис­сов) включает альтернативы, ко­торые всегда более предпоч­ти­те­ль­ны по срав­не­­нию с любой аль­тернативой из множества А\А *. При этом лю­бые две аль­те­рнати­вы из множества Парето по предпочтению не­сра­в­нимы. Альтер­на­ти­вы 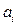и 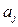называются не­сравнимыми, если альтернати­ва пре­во­схо­дит аль­тер­нативу по одним критериям, а альтернатива пре­во­схо­дит аль­те­р­на­ти­ву по другим. Выражение К(а*) > К(а) означает, что

и хотя бы одно из этих неравенств является строгим.

Понятие множества Парето можно пояснить на примере. Пусть имеем задачу оп­тимизации по двум критериям , 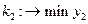где и - по­ка­за­те­ли свойств системы (параметры), значения которых можно выбирать. Це­лью является выбор оптимальных (в данном случае минимальных) зна­чений параметров. Если изобразить множество критериев в виде многоугольника (Рис. 3‑2):

 

Рис. 3‑2. Множество Парето

и рассмотреть пару точек и 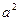как показано на рисунке, то легко заметить, что для этих точек справедливо:

т.е., точка является более предпочтительной по отношению к точке 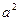. По­э­тому оставлять для рассмотрения точку 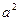не имеет смысла.

Продолжая рассмотрение других точек области многоугольника, придем к то­му, что для выбора остаются только точки стороны AE. Для каждой пары этих точек предпочтение по одному показателю со­про­во­ж­да­ется ухудшением по другому.

Методы, основанные на свертке векторного критерия в скалярный, пре­д­по­ла­га­ют переход к решению задачи

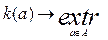
где - скалярный критерий, представляющий собой некоторую функцию от значений компонентов векторного критерия:

Основной проблемой этого подхода является пост­роение функции f, назы­ва­е­мой сверткой. Свертка производится в несколько этапов.

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: