Порядок расчета вероятностной модели методом PERT

После того, как осуществлена нумерация вершин и собраны данные по tmax и tmin проводятся следующие расчеты.

1) Вершины графа нумеруются;

2) Для всех работ собираются данные по tmax и tmin;

3) Определяются моменты распределений длительностей работ tож(i,j), ;

4) На основании совокупности значений t(i,j) = tож(i,j) проводится обыч­ный расчет характеристик, как для детерминированной сетевой модели;

5) Определяется критический путь Lкр и его среднее значение

6) Определяется дисперсия длительностей Lкр как сумма дисперсий дли­те­ль­но­­стей критических ра­бот (предположение о независимости работ)

7) Поскольку длительности t(i,j) – независимые случайные величины, их сумма Tкр может тракто­ваться как случайная величина, распре­де­лен­ная по нор­ма­ль­но­му закону 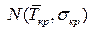с матожи­да­ни­ем и дис­пер­си­­ей , для ко­то­ро­го фу­н­кция плотности вероятности имеет вид:

8) Поскольку из свойств нормального распределения следует (правило «трех си­гма»), что с вероят­но­с­тью 0,9974 значение Ткр будет нахо­ди­ть­ся в интервале

,

можно утверждать, что

,

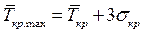
9) Пусть определен некоторый плановый срок выполнения всего проекта – Тпл.

Вероят­ность P (Tкр ≤ Tпл) выполнения работы в срок определяется сле­ду­ю­щим образом:

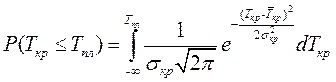
Для того, чтобы получить конкретные значения для этой функции, не­об­хо­ди­­мо перейти от 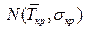к ста­ндартному табулированному ра­спре­де­ле­­нию . С этой целью осуществляется замена переменной:

что приводит к изменению подинтегральной функции и пределов интегрирования:

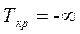
y=0

Тогда

и

где Ф(х) называется функцией Лапласа и табулирована. Значение ее мо­ж­но та­к­­же получить с ис­по­льзованием библиотечных функций, ко­то­рые при­­сут­ствуют во многих компиляторах и про­г­рам­м­ных пакетах. В час­т­но­сти, в таб­ли­чном процессоре Microsoft Excel она представлена функцией нормстрасп().

Содержание работы

Вариант работы определяется порядковым номером студента в списке группы.

Работа выполняется с помощью табличного редактора Microsoft Excel.

1. Согласно указаниям столбца Топология таблицы вариантов работ по­ст­рой­те сетевой граф для своего варианта работы.

В записи, определяющей вид графа, используется следующая нотация.

A-B Граф образуется из частичных графов A и B таким об­разом, что сли­­ва­ются правая вершина частичного графа с но­ме­ром A и левая ве­­р­ши­на частичного графа с номером B, а все дуги остаются в об­ра­зо­ванном графе.

Например, обозначение 2-3 в результате дает граф:

(A:B) Граф образуется из частичных графов A и B таким образом, что сливаются правая вершина частичного графа с номе­ром A и правая ве­­ршина частичного графа с номером B, левая вер­ши­на частичного гра­фа с номером A и левая вершина частичного гра­фа с номером B, а все дуги остаются в образованном графе.

Например, обозначение (2:3) подразумевает граф:

Поскольку такой граф недопустим (две работы начинаются и за­ка­н­чи­ваются в одной и той же паре вершин), то такой граф требуется пре­образовать, например, так:

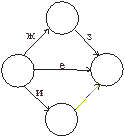
Для исключения неоднозначности здесь добавлена фиктивная работа.

Желательно готовить электронный вариант изображения графа в каком-ли­бо графическом редакторе (например, MS Visio).

2. Пронумеруйте вершины графа, используя алгоритм вычеркивания дуг.

3. В приложении Microsoft Excel подготовьте таблицу следующего вида

Код	i	j	Tмин(ij)	Tмакс(ij)	Tож(ij)	σ2(ij)
a
b
…	..	..	…	…	…..	…

В ячейках каждой строки таблицы размещаются:

Код - код работы

i - номер начальной вершины работы, обозначенной кодом

j - номер конечной вершины работы, обозначенной кодом

Tмин(ij) – минимальная продолжительность работы, значение берется из та­­б­­ли­цы для минимальных продолжительностей работ из ячей­ки, сто­я­щей на пересечении строки с кодом работы и столбца с но­ме­ром, указанном в ячейке на пересечении столбца Tмин и строки с но­мером варианта таблицы вариантов.

Tмакс(ij ) – максимальная продолжительность работы, значение берется из таб­ли­цы для максимальных продолжительностей работ из ячей­ки, сто­­я­щей на пересечении строки с кодом работы и столбца с но­ме­ром, указанном в ячейке на пересечении столбца Tмакс и стро­ки с но­мером варианта таблицы вариантов

Tож(ij) – мате­матическое ожидание продолжительности работы, зна­че­ние рассчитывается на основании выражения раздела 4.2.7

σ2(ij) – дисперсия продолжительности работы, значение рассчиты­вает­ся на основании выражения раздела 4.2.7

Заполните таблицу числовыми значениями для своего варианта.

4. Подготовьте таблицу для расчета детерминированной модели:

i	j	Tрн(ij)	Tож(ij)	Tро(ij)	Tпн(ij)	Tож(ij)	Tпо(ij)	Rп(ij)

Для каждой работы внесите в таблицу рассчитанные в предыдущем пун­к­те значения T ож (ij) и выражения для нахождения T ро (ij),T пн (ij),R п (ij).

5. С помощью таблицы проведите расчет детерминированной модели.

6. С использованием полученных результатов проведите расчет параметров вероят­но­стной модели:

Ткр.ож = _______

σ 2кр = _______

Ткр.мин = _______

Ткр.макс = _______

Тпл1 = _______

P(Тпл1> Т кр) = _______

Тпл2 = _______

P(Тпл2> Т кр) = _______

Оценивание P(Т пл>Т кр) проводится для двух значений плановых сроков Тпл1 и Тпл2. В качестве Тпл1 и Тпл2 берутся значения:

1) Тпл 1= Entier (Ткр.ож / 5) * 5.

2) Тпл2 = Entier (Ткр.ож / 5) *5+5

Например, если Ткр.ож =98, то следует взять

1) Тпл1=95;

2) Тпл2=100

Отчет по работе

Отчет по работе должен включать исходные данные и результаты.

1. Таблицу с исходными данными варианта.

№	Топология	Строка таблицы Tмин	Строка таблицы Tмакс

 

Таблица содержит одну строку – копию из таблицы раздела 4.6 с дан­ны­ми варианта работы.

2. Таблицу с временными параметрами работ (см. раздел 4.3)

3. Таблицу с временными параметрами детермини­ро­ванной модели (см. раз­дел 4.3)

4. Результаты расчета временных параметров вероят­но­стной модели (см. ра­з­дел 4.3)

4.5 Контрольные вопросы

1) Что называется сетевой моделью?

2) Какие задачи решаются с помощью сетевой модели?

3) Как определяется событие?

4) Что называется работой?

5) Что такое фиктивное работа и для чего она используется?

6) В чем заключается суть алгоритма расстановки пометок?

7) Что такое путь?

8) Какой путь называется критическим, каков его физический смысл?

9) Какие временные параметры событий используются для описания се­те­вой модели?

10) Какие временные параметры работ используются для описания сете­вой модели?

11) В чем могут состоять отличия вероятностной сетевой модели от де­тер­минированной?

12) На каких предположениях основан метод расчета вероятностных мо­де­лей с помощью средних?

13) Из каких основных шагов состоит метод расчета вероятностных мо­де­лей с помощью средних?

Варианты

Варианты задания

№	Топология	Строка таблицы Tмин	Строка таблицы Tмакс
	(1: 2) – 3 – 4 – 5
	1 – (2: 5) – 3 – 4
	3 – 4 – (1: 5) – 2
	(2: 3) – (1: 4) – 5
	5 – (1: 4) – 3 – 2
	4 – (1: 2) – 5 – 3
	(1: 4) – 5 – 3 – 2
	4 – (5: 1) – 2 – 3
	2 – 3 – 5 – (4: 1)
	4 –3 – (2: 5) – 1
	3 – 4 – (2: 1) – 5
	(5: 3) – (2: 4) – 1
	3 – (4: 5) – 1 – 2
	1 – 2 – 3 – (5: 4)
	5 – 4 – 3 – (1: 2)
	3 – 4 – 5 – (1: 2)
	3 – (2: 5) – 4 – 1
	(4: 5) – 1 – 3– 2
	2 – 1 – (4: 5) – 3
	(2: 5) – 1 – 4 – 3
	2 – 5 – (1: 4) – 3
	(1: 4) – 2 – 3 – 5
	3 – 1 – (2: 5) – 4
	(5: 1) – 4 – 2 – 3
	2 – 3 – (1: 5) – 4
	4 – 3 – 2 – (1: 5)
	(2: 4) – 5 – 3 – 1
	2 – 5 – 3 – (1: 4)
	3 – (1: 5) – 4 – 2
	5 – 3 – (2: 4) – 1

 

Частичные сетевые графики

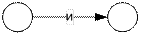
Минимальные оценки длительности работ Tмин

а

б

в

г

д

е

ж

з

и

к

л

м

н

о

п

р

 

Максимальные оценки длительности работ Tмакс

а

б

в

г

д

е

ж

з

и

к

л

м

н

о

п

р

 

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: