Временные параметры событий

Ранний срок:

tp(i)=max(T(L(I,i))

Поздний срок:

tп(i) = Tкр- T (max L(i,C)) = min(Tкр-T (L(i,C)))

Резерв событияR(i), или резерв времени:

R(i)= tп(i) - t p(i)

Временные параметры работ

Ранний срок начала tpн(i,j) (раннее начало):

tpн(i,j) = tp(i)

Ранний срок окончания(ранее окончание):

tpо(i,j) = tpн(i,j) + t(i,j) = tp(i) + t(i,j)

Поздний срок окончанияt по(i,j) (позднее окончание):

tпо(i,j) = tп(j)

Поздний срок начала tпн(i,j) (позднее начало):

tпн(i,j)= tп(j)- t (i,j)

Резерв работы(полный резерв):

Rп(i,j) = tп(j) - tр(i)- t(i,j)

Порядок расчета детерминированной сетевой модели

Графический метод

Метод основан на использовании графа модели, где вершины для удобства ра­з­де­лены на четыре сектора для записи значений:

i – номер события,

tp(i) – раннее время события

tп(i) – позднее время события

R(i) – резерв

Процесс расчета сетевой модели начинается с нумерации событий, затем осу­ще­ст­вляется по­сле­­довательный проход по цепочке событий справа налево с за­по­л­нением поля tp(i), затем – обратный проход с заполнением поля tп(i). После это­го запол­ня­ется поле R(i).

При заполнении полей tp(i) и tп(i) вместо используются рекуррентные формулы:

tp(j) = max{ tp(i)+ t (ij), … tp(l)+ tp(lj)}

tп(j) = min{ tп(m) - tp(jm), … tп(k) - tp(jk)}

что позволяет свести процесс к просмотру окрестностей текущего события.

Табличный метод

Табличный метод основан на использовании более детализиро­ван­ного по сра­внению с информацией о событиях реестра работ, представленного в виде та­блицы с вре­ме­н­ными характеристики работ, например:

Работы	Временные характеристики работ
i	j	t рн(i,j)	t(i,j)	t ро(i,j)	t пн(i,j)	t(i,j)	t по (i,j)	R п(i,j)
Порядок заполнения колонок

 

В нижней строке таблицы указан порядок выполнения расчетов, включающий:

- нумерацию событий (i,j);

- занесение в таблицу длительностей работ t(i,j) (колонки дублируются, что­бы облегчить последую­щее заполнение колонок tро(i,j) и tпн(i,j);

- сортировка строк в лексикографическом порядке (десятичные числа, обра­зу­емые парами (i,j) должны возрастать);

- проход слева направо и заполнение колонок tрн(i,j) и tро(i,j) (tро(i,j) = tрн(i,j) + t (i,j) );

- проход справа налево и заполнение колонок tпо(i,j) и tпн(i,j) (tпн(i,j) = tпо(i,j) - t (i,j) );

- заполнение колонки Rп(i,j).

Вероятностная сетевая модель

В реальной дейст­ви­те­ль­ности имеет место неопределенность как в структуре гра­фа (те или иные события или работы могут при­сутствовать или же нет), так и во временных параметрах - времена выполнения работ, моменты на­сту­п­ления событий, резервы и пр. Одним из распространенных методов расчета является метод PERT , использующий ряд упрощающих предположений по сравнению с общей постанов­кой задачи ра­счета вероятностных сетей:

1) Предполагается, что времена работ t(i,j) подчиняются β-распределению, в котором параметры αijи γijодинаковы для всех работ, причем

αij=α =1

γij=γ=2

Тогда функция распре­деле­ния длительности работы (i,j) принимает вид:

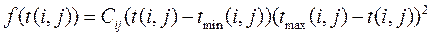
где

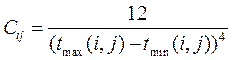
Для таких распределений в качестве приближенных значений для моментов могут быть приняты следующие оценки

Математическое ожидание:

Дисперсия:

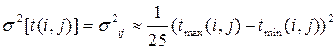
2) Предполагается статистическая независимость длительностей работ.

3) Предполагается, что длительность критического пути настолько пре­во­с­хо­дит (в среднем) дли­те­ль­ности прочих полных путей, что практически невоз­мо­жен его случайный «перескок» на другие пути.

---

Рекомендуемые страницы:

Воспользуйтесь поиском по сайту: