Оценивание в условиях риска

Для каждого варианта приводятся:

- значения вероятностей появления исхода для каждой аль­те­р­на­ти­вы 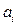(таблица),

- значения показателей исходов для каждой альтернативы (под таблицами).

 

	p (yk / ai)
a1	0.30
0.40
0.30
a2	0.20
0.65
0.15
a3	0.25
0.60
0.15

F(y1)= 0.70

F(y2)= 0.50

F(y3)= 0.60

	p (yk / ai)
a1	0.20
0.50
0.30
a2	0.40
0.50
0.10
a3	0.15
0.30
0.55

F(y1)= 0.90

F(y2)= 0.60

F(y3) = 1.0

	p (yk / ai)
a1	0.20
0.50
0.30
a2	0.40
0.50
0.10
a3	0.15
0.30
0.55

F(y1)= 0.7

F(y2)= 0.5

F(y3)= 0.6

	p (yk / ai)
a1	0.30
0.40
0.30
a2	0.20
0.65
0.15
a3	0.25
0.60
0.15

F(y1)= 0.9

F(y2)= 0.6

F(y3)= 1.0

	p (yk / ai)
a1	0.30
0.20
0.50
a2	0.55
0.35
0.10
a3	0.25
0.60
0.15

F(y1)= 0.7

F(y2)= 0.5

F(y3)= 0.6

	p (yk / ai)
a1	0.30
0.40
0.30
a2	0.20
0.65
0.15
a3	0.25
0.60
0.15

F(y1)= 1.2

F(y2)= 0.6

F(y3)= 1.0

	p (yk / ai)
a1	0.30
0.40
0.30
a2	0.20
0.65
0.15
a3	0.45
0.45
0.10

F(y1)= 1.2

F(y2)= 0.8

F(y3)= 1.0

	p (yk / ai)
a1	0.25
0.45
0.30
a2	0.50
0.35
0.15
a2	0.25
0.60
0.15

F(y1)= 3.2

F(y2)= 2.4

F(y3)=3.5

	p (yk / ai)
a1	0.55
0.30
0.15
a2	0.25
0.55
0.20
a3	0.25
0.60
0.15

F(y1)= 0.9

F(y2)= 0.6

F(y3)=1.0

	p (yk / ai)
a1	0.30
0.20
0.50
a2	0.55
0.35
0.10
a3	0.25
0.60
0.15

F(y1)= 0.7

F(y2)= 0.5

F(y3)= 0.6

	p (yk / ai)
a1	0.30
0.40
0.30
a2	0.25
0.45
0.30
a3	0.55
0.30
0.15

F(y1)= 1.2

F(y2)= 0.6

F(y3)=1.0

	p (yk / ai)
a1	0.20
0.50
0.30
a2	0.40
0.50
0.10
a3	0.15
0.30
0.55

F(y1)= 1.6

F(y2)= 1.9

F(y3)=2.0

	p (yk / ai)
a1	0.30
0.40
0.30
a2	0.20
0.65
0.15
a3	0.25
0.60
0.15

F(y1)= 4.9

F(y2)= 5.6

F(y3)=4. 0

	p (yk / ai)
a1	0.50
0.25
0.25
a2	0.40
0.45
0.15
a3	0.45
0.30
0.25

F(y1)= 1.2

F(y2)= 0.8

F(y3)=1.0

	p (yk / ai)
a1	0.25
0.45
0.30
a2	0.50
0.35
0.15
a3	0.25
0.60
0.15

F(y1)= 0.8

F(y2)= 0.6

F(y3)=1.0

	p (yk / ai)
a1	0.55
0.30
0.15
a2	0.25
0.55
0.20
a3	0.25
0.60
0.15

F(y1)= 0.9

F(y2)= 1.0

F(y3)=1.3

	p (yk / ai)
a1	0.30
0.40
0.30
a2	0.20
0.65
0.15
a3	0.45
0.45
0.10

F(y1)= 3.2

F(y2)= 2.8

F(y3)=2.9

	p (yk / ai)
a1	0.25
0.45
0.30
a2	0.50
0.35
0.15
a3	0.25
0.60
0.15

F(y1)= 5.2

F(y2)= 3.4

F(y3)=4.5

	p (yk / ai)
a1	0.30
0.40
0.30
a2	0.20
0.65
0.15
a3	0.15
0.70
0.15

F(y1)= 1.9

F(y2)= 3.6

F(y3)=4.0

	p (yk / ai)
a1	0.10
0.50
0.40
a2	0.50
0.35
0.15
a2	0.25
0.60
0.15

F(y1)= 0.9

F(y2)= 0.6

F(y3)=1.0

	p (yk / ai)
a1	0.20
0.50
0.30
a2	0.20
0.65
0.15
a3	0.25
0.60
0.15

F(y1)= 2.8

F(y2)= 3.6

F(y3)=4.0

	p (yk / ai)
a1	0.30
0.20
0.50
a2	0.55
0.35
0.10
a3	0.25
0.60
0.15

F(y1)= 1.7

F(y2)= 2.5

F(y3)=0.6

	p (yk / ai)
a1	0.25
0.45
0.30
a2	0.50
0.35
0.15
a3	0.25
0.60
0.15

F(y1)= 7.6

F(y2)= 6.6

F(y3)=8.0

	p (yk / ai)
a1	0.55
0.30
0.15
a2	0.25
0.55
0.20
a3	0.25
0.60
0.15

F(y1)= 1.7

F(y2)= 2.1

F(y3)=3.7

	p (yk / ai)
a1	0.50
0.35
0.15
a2	0.25
0.40
0.35
a3	0.10
0.50
0.40

F(y1)= 1.7

F(y2)= 2.2

F(y3)=0.6

Оценивание в условиях неопределенности

Для каждого варианта приводятся:

- матрица значений Kijэффек­ти­в­но­сти применения аль­тернативы aiдля внеш­него воздействия Nj(первые пять строк таблицы);

- веро­ят­но­сти pjпоявления каждого из воздействий Nj(по­сле­дняя стро­ка таб­лицы);

- коэффициенты оптимизма a1и a2(записаны под таблицей) для двух ва­­­риантов оце­ни­вания по критерию Гурвица).

	N1	N2	N3	N4	N5	N6
a1	13,1	9,8	23,3	17,7	19,9	16,4
a2	15,7	10,1	16,8	13,3	15,5	16,9
a3	10,4	9,7	23,6	17,0	21,3	15,0
a4	17,6	7,8	19,6	17,7	19,9	18,3
a5	19,2	8,4	21,4	15,8	16,7	20,0
Pj	0,10	0,11	0,32	0,11	0,24	0,12

a1= 0,1 a2= 0,9

	N1	N2	N3	N4	N5	N6
a1	9,7	22,3	17,7	18,8	14,3	13,1
a2	10,2	16,8	13,3	14,6	16,9	15,7
a3	9,7	22,2	17,0	22,3	11,9	10,4
a4	7,8	21,6	17,7	19,8	17,3	17,6
a5	7,5	22,4	14,8	17,6	21,0	19,2
Pj	0,20	0,09	0,12	0,25	0,11	0,23

a1=0,1 a2=0,9

	N1	N2	N3	N4	N5	N6
a1	12,3	9,7	17,7	18,8	14,3	13,1
a2	14,8	10,2	13,3	14,6	16,9	15,7
a3	13,4	9,7	17,0	19,4	11,9	10,4
a4	15,6	7,8	18,7	19,4	17,3	17,6
a5	16,4	7,5	15,8	18,6	19,0	19,2
Pj	0,11	0,15	0,20	0,21	0,10	0,23

a1=0,4 a2=0,6

	N1	N2	N3	N4	N5	N6
a1	10,4	15,7	10,3	13,1	13,3	14,4
a2	17,6	10,4	17,6	15,7	15,7	13,3
a3	17,3	17,6	19,2	14,7	15,7	16,9
a4	15,7	18,9	17,3	19,3	10,4	11,8
a5	12,0	15,7	17,8	18,9	17,6	17,0
Pj	0,12	0,19	0,11	0,23	0,22	0,13

a1=0,4 a2=0,6

	N1	N2	N3	N4	N5	N6
a1	9,4	15,7	14,4	15,1	18,4	17,5
a2	11,6	12,4	17,6	15,7	17,3	15,3
a3	13,2	17,6	18,2	14,6	17,0	15,8
a4	8,7	19,9	17,3	18,3	18,0	14,8
a5	11,9	15,7	17,8	17,9	19,3	17,6
Pj	0,12	0,26	0,11	0,23	0,03	0,25

a1=0,4 a2=0,6

	N1	N2	N3	N4	N5	N6
a1	13,4	15,5	14,6	15,5	18,4	17,3
a2	12,6	12,7	17,6	15,6	17,1	15,7
a3	13,2	17,6	18,3	14,5	16,9	14,9
a4	10,7	19,8	17,9	18,6	15,9	13,3
a5	15,0	13,3	17,8	17,7	19,6	17,6
Pj	0,12	0,19	0,31	0,23	0,03	0,12

a1=0,3 a2=0,8

	N1	N2	N3	N4	N5	N6
a1	13,2	17,4	18,3	14,5	16,9	14,9
a2	10,7	19,7	17,9	18,6	15,9	13,3
a3	15,0	13,3	17,8	17,7	19,1	17,6
a4	13,4	15,5	14,6	15,5	18,4	17,3
a5	12,6	12,7	17,6	15,6	17,1	15,7
Pj	0,11	0,20	0,29	0,24	0,04	0,12

a1=0,9 a2=0,4

	N1	N2	N3	N4	N5	N6
a1	18,3	17,4	13,2	14,1	14,9	16,9
a2	17,9	14,7	10,7	18,6	13,3	15,9
a3	17,8	13,0	15,0	17,7	17,1	17,6
a4	16,6	15,5	13,4	14,1	17,3	18,4
a5	17,6	12,7	12,6	15,6	15,7	17,1
Pj	0,20	0,18	0,11	0,05	0,12	0,34

a1=0,9 a2=0,5

	N1	N2	N3	N4	N5	N6
a1	14,2	15,5	13,4	16,6	17,3	18,4
a2	18,7	12,7	12,6	17,6	15,7	17,1
a3	17,8	13,0	15,0	17,8	17,1	17,6
a4	14,1	12,7	12,6	17,6	15,7	17,1
a5	15,6	15,5	13,4	16,6	17,3	18,4
Pj	0,08	0,17	0,12	0,20	0,12	0,31

a1=0,8 a2=0,2

	N1	N2	N3	N4	N5	N6
a1	15,6	15,6	13,4	16,6	17,3	18,4
a2	17,1	15,7	12,7	17,6	15,7	18,7
a3	17,6	17,1	13,0	17,8	17,1	17,8
a4	17,1	15,7	12,7	17,6	15,7	14,1
a5	14,2	15,5	13,4	16,6	17,3	18,4
Pj	0,31	0,12	0,17	0,20	0,12	0,08

a1=0,8 a2=0,4

	N1	N2	N3	N4	N5	N6
a1	15,7	12,7	17,6	15,7	18,7	18,4
a2	17,1	13,0	16,2	16,1	17,8	18,7
a3	15,7	12,7	17,6	15,7	14,1	18,8
a4	15,5	13,4	16,6	17,3	18,4	14,1
a5	14,2	15,5	13,4	16,6	17,3	18,4
Pj	0,21	0,18	0,25	0,16	0,12	0,08

a1=0,8 a2=0,1

	N1	N2	N3	N4	N5	N6
a1	15,8	12,3	15,7	17,6	18,7	18,4
a2	17,2	12,3	16,1	16,1	17,8	18,7
a3	15,8	12,6	15,7	17,6	14,1	18,8
a4	15,1	12,4	17,3	16,6	18,4	14,1
a5	14,5	15,5	16,6	13,4	17,3	18,4
Pj	0,26	0,25	0,12	0,16	0,08	0,13

a1=0,7 a2=0,3

	N1	N2	N3	N4	N5	N6
a1	23,3	17,7	19,9	16,4	13,1	9,8
a2	16,8	13,3	15,5	16,9	15,7	10,1
a3	23,6	17,0	21,3	15,0	10,4	9,7
a4	19,6	17,7	19,9	18,3	17,6	7,8
a5	21,4	15,8	17,7	20,0	19,2	8,4
Pj	0,32	0,11	0,24	0,12	0,10	0,11

a1=0,2 a2=0,9

	N1	N2	N3	N4	N5	N6
a1	14,3	13,1	17,7	18,8	9,7	22,3
a2	16,9	15,7	13,3	14,6	10,2	16,8
a3	14,9	10,4	17,0	22,3	9,7	22,2
a4	17,3	17,6	17,7	19,8	7,8	21,6
a5	21,0	19,2	14,8	17,6	7,5	22,4
Pj	0,11	0,23	0,12	0,25	0,20	0,09

a1=0,1 a2=0,9

	N1	N2	N3	N4	N5	N6
a1	13,3	14,6	16,9	15,7	14,8	10,2
a2	17,0	19,4	11,9	10,4	13,4	9,7
a3	18,7	19,4	17,3	17,6	15,6	7,8
a4	15,8	18,6	19,0	19,2	16,4	7,5
a5	17,7	18,8	14,3	13,1	12,3	9,7
Pj	0,20	0,21	0,10	0,23	0,11	0,15

a1=0,4 a2=0,6

	N1	N2	N3	N4	N5	N6
a1	14,4	17,6	17,6	15,7	15,7	13,3
a2	17,6	17,2	17,3	14,7	15,7	16,9
a3	15,7	10,3	10,4	13,1	13,3	14,4
a4	18,9	17,3	15,7	19,3	10,4	11,8
a5	15,7	17,8	12,0	18,9	17,6	17,0
Pj	0,19	0,11	0,12	0,23	0,22	0,13

a1=0,3 a2=0,8

	N1	N2	N3	N4	N5	N6
a1	13,2	17,6	18,2	13,6	17,0	15,8
a2	8,7	19,9	17,3	18,3	18,0	14,8
a3	9,4	15,7	14,4	15,1	18,4	17,5
a4	11,6	12,4	17,6	15,7	17,3	15,3
a5	11,9	15,7	17,8	17,9	19,3	17,6
Pj	0,12	0,27	0,11	0,23	0,03	0,24

a1=0,4 a2=0,6

 

	N1	N2	N3	N4	N5	N6
a1	13,4	15,5	14,6	15,5	18,4	13,4
a2	10,7	19,8	17,9	18,6	15,9	10,7
a3	13,2	17,6	18,3	14,5	16,9	13,2
a4	12,6	12,7	17,6	15,6	17,1	12,6
a5	15,0	13,3	17,8	17,7	19,6	15,0
Pj	0,12	0,19	0,31	0,23	0,03	0,12

a1=0,2 a2=0,8

 

	N1	N2	N3	N4	N5	N6
a1	14,6	15,5	18,4	17,3	13,4	15,5
a2	17,6	15,6	17,1	15,7	12,6	12,7
a3	17,9	18,6	15,9	13,3	10,7	19,7
a4	17,8	15,5	19,1	17,6	15,0	13,3
a5	18,3	15,5	16,9	14,9	13,2	17,4
Pj	0,29	0,24	0,04	0,12	0,11	0,20

a1=0,9 a2=0,4

	N1	N2	N3	N4	N5	N6
a1	15,0	15,5	17,1	17,6	17,8	13,0
a2	13,4	14,1	17,3	18,4	16,6	15,5
a3	12,6	15,6	15,7	17,1	17,6	12,7
a4	13,2	14,1	14,9	16,9	18,3	17,4
a5	10,7	18,6	13,3	15,9	17,9	14,7
Pj	0,15	0,05	0,12	0,34	0,20	0,14

a1=0,9 a2=0,5

 

	N1	N2	N3	N4	N5	N6
a1	17,6	13,0	15,0	17,8	17,1	17,8
a2	18,4	15,5	13,3	16,6	17,3	14,2
a3	17,1	12,7	12,6	17,6	15,7	18,7
a4	17,1	14,7	12,6	17,6	15,7	14,1
a5	18,4	15,5	13,2	16,6	17,3	15,6
Pj	0,31	0,17	0,12	0,20	0,12	0,08

a1=0,8 a2=0,2

 

	N1	N2	N3	N4	N5	N6
a1	17,1	17,1	13,0	17,8	16,8	17,6
a2	15,7	15,7	12,7	17,6	14,1	17,1
a3	17,3	15,6	13,4	16,6	18,4	15,6
a4	15,7	15,7	12,7	17,6	18,7	17,1
a5	17,3	15,5	13,4	16,6	18,4	14,2
Pj	0,12	0,12	0,17	0,20	0,08	0,31

a1=0,8 a2=0,4

 

 

Литература

	Анфилатов В.С., Емельянов А.А., Кукушкин А.А., Системный анализ в управлении. Учебное пособие. – М.: Финансы и статистика, 2005.
	Теория систем и системный анализ в управлении организациями / Под ред. В.Н. Волковой и А.А. Емельянова. – М.: Финансы и статистика, 2006.
	Саати Т. Принятие решений. Метод анализа иерархий. – М.: Радио и связь, 1993
	Т.Л.Партыка, И.И.Попов Математические методы – М., ФОРУМ – ИНФРА-М, 2005
	Моудер Дж., Филлипс С. Метод сетевого планирования и организации работ (Перт) – М-Л,: Энергия 1966
	Технологии принятия решений: метод анализа иерархий. ЗАО «Нейросплав» –http://data.mf.grsu.by/citforum/htdocs/consulting/BI/resolution/index.shtml
	О. А. Ахметов, М. Б. Мжельский Метод анализа иерархий как сос­та­в­ная часть методологии проведения оценки недвижимости ООО «Си­бирс­кий Центр Оценки», г.Новосибирск –http://www.nsk.su/~estate/articles/art001.html

 

⇐ Предыдущая12345678

Поделиться:

Воспользуйтесь поиском по сайту: