Обоснование допустимости свертки

Требует подтвержде­ния, что рассматриваемые показатели эффективности яв­ля­ются однородными. Известно, что показатели эффективности разде­ляются на три группы: показатели результативности, ресурсоем­кости и опе­ра­ти­в­но­сти. В общем случае разрешается свертка по­казателей, входящих в обоб­ще­н­ный показатель для каждой груп­пы отдельно. Свертка показателей раз­ных групп может привести к потере физического смысла такого критерия.

Нормализация критериев.

Проводится аналогично нормиров­ке показателей.

Учет приоритетов критериев.

Осуществляется в большин­стве методов свертывания путем задания вектора ко­эффициен­тов важности критериев l:

.

где - коэффициент важности критерия , обычно совпадающий с коэф­фи­ци­ентом значимости частного показателя качества.

Определение коэффициентов важности критериев, как и в слу­чае с пока­за­те­ля­ми, сталкивается с серьезными трудностями и сводится либо к исполь­зо­ва­нию формальных процедур, либо к применению экспертных оценок.

В результате нормализации и учета приоритетов критериев вместо исходной ве­кторной оценки К(а) альтернативы а образу­ется новая векторная оценка

где 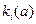- нормированный критерий, он находится аналогично нормирован­ному показателю. Именно эта полученная векторная оценка подлежит пре­об­ра­­зованию с использованием функции свертки.

Свертка показателей.

Способ свертки зависит от характера показателей и целей оценивания сис­тем. Известны несколько ви­дов свертки. Наиболее часто использую адди­тив­ная и мультипликативная све­р­тки компонентов векторного критерия.

Аддитивная свертка компонентов векторного критериясостоит в пред­став­ле­нии обобщенного скалярного критерия в виде суммы взвешенных нор­ми­ро­ванных частных критериев:

(3‑1)

Такие критерии образуют группу аддитивных критериев, их свертка ос­но­вана на использовании принципа справедливой компенсации абсо­лю­т­ных зна­че­ний нормированных частных критериев. Сутью этого принципа яв­ля­ет­ся ут­вер­ждение: справедливым следует считать такой компромисс, при кото­ром су­м­марныйуровень абсолютного снижения значений одного или нес­ко­ль­ких по­казателей не превышает суммарного уровня абсолютного увели­че­ния зна­че­ний других показателей. Главный недостаток аддитивных крите­риев со­сто­ит в том, что они не вытекают из объективной роли частных кри­териев в оп­ре­де­лении качества системы и поэтому выступают как фо­р­ма­ль­ный матема­ти­че­ский прием, придающий задаче удобный вид.Кроме того, низ­кие оценки по одним критериям могут компенсироваться высокими оцен­ка­ми по другим кри­териям. Это значит, что уменьшение одного из критериев вплоть до ну­ле­во­го значения может возмещаться возрастанием другого.

Мультипликативная свертка критерия состоит в представлении обобщен­но­го скалярного критерия в виде произведения:

(3‑2)

Мультипликативный критерий образуется путем перемножения частных кри­те­риев возведенных в степени . Если все частные критерии имеют оди­наковую важность, то =1. При разной важности критериев ≠1.

В мультипликативных критериях компромисс достигается по отношению не к абсолютным, а к относительным изме­нениям частных критериев, а именно, сум­марный уровень относительного снижения значений одного или нес­ко­ль­ких критериев не превышает суммарного уровня относи­тельного увеличения зна­­чений других критериев.

Достоинством мультипликативного критерия является то, что при его ис­по­ль­зовании не требуется нормировки частных критериев. К его недостаткам от­носится то, что он компенсирует недо­статочную величину одного частного кри­терия избыточной ве­личиной другого и имеет тенденцию сгла­живать уро­в­ни частных критериев за счет неравнозначных первоначальных значений ча­с­тных критериев.

Выбор между аддитивной и мультипликативной свертками частных кри­те­ри­ев определяется степенью важности абсолютных или относительных изме­не­ний значений частных критериев со­ответственно.

Содержание работы

В работе необходимо провести оценивание шести систем по четырем кри­те­ри­ям качества. В качестве исходных данных задаются:

- условие оптимальности (max или min) для каждого критерия;

- вектор приоритетов критериев l =(l1,… l4);

- вектор значений критериев ) для каждого оцениваемого образца.

Вариант исходных данных определяется порядковым номером студента в спи­ске группы.

1) Откройте приложение Microsoft Excel.

2) Подготовьте рабочую таблицу со структурой, показанной на Рис. 3‑3:

В ячейки подраздела Натуральные раздела Критерии заносятся ис­хо­д­ные дан­ные .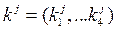

Ячейки подраздела Формула A раздела Критерии предназначены для занесения в них нормированных значений критериев, вычисленных по формуле:

 

Критерии

Парето

Оптимальность

Превосходство

Аддитивная свертка

Мультипликативная свертка

Натуральные

Формула A

Формула B

Формула A

Формула B

li=1

l≠1

k1

k2

k3

k4

k1

k2

k3

k4

k1

k2

k3

k4

К

К*

К

К*

К

К*

К

К*

 

Рис. 3‑3. Структура Excel-таблицы для проведения расчетов по оцениванию систем

Ячейки подраздела Формула A раздела Критерии предназначены для занесения в них нормированных значений критериев, вычисленных по формуле:

В ячейки столбца Парето заносятся:

В ячейки столбца Оптимальность заносятся:

В ячейки столбца Превосходство заносятся:

Ячейки подраздела Формула A раздела Аддитивная свертка пред­назна­чены для занесения в них скалярных значений критериев, вычи­сленных по формуле (3‑1) на основе значений критериев, нормированных на ос­нове формулы A. В столбце K заполняются все ячейки, столбце K* за­по­л­­няются ячейки для систем (строк), входящих в множество Парето.

Ячейки подраздела Формула B раздела Аддитивная свертка пред­назна­че­ны для занесения в них скалярных значений критериев, вычи­сленных по формуле (3‑1) на основе значений критериев, нормированных на ос­нове формулы B. В столбце K заполняются все ячейки, в столбце K* за­по­л­­няются ячейки для систем (строк), входящих в множество Парето.

Для вычисления значения скалярного критерия используются значения при­оритета , заданные в исходных данных 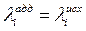, где - зна­че­ние приоритета, заданное в исходных данных.

Ячейки подраздела l=1 раздела Мультипликативная свертка пред­наз­на­­­чены для занесения в них скалярных значений критериев, вычи­слен­ных по формуле (3‑2) в предположении равных приоритетов кри­териев (li=1). В столбце K заполняются все ячейки, в столбце K* запол­няются яче­й­ки для систем (строк), входящих в множество Парето.

Ячейки подраздела l≠1 раздела Мультипликативная свертка пред­назна­чены для занесения в них скалярных значений критериев, вычи­сленных по формуле (3‑2) в предположении равных приоритетов кри­териев. В сто­лбце K заполняются все ячейки, в столбце K* запол­няются ячейки для систем (строк), входящих в множество Парето. Приоритеты критериев на­значаются по правилу:

где

- значение приоритета, заданное в исходных данных

-минимальное значение, заданное в исходных данных

3) Проведите все необходимые расчеты (заполните все ячейки с вычи­сляе­мы­ми значениями необходимыми выражениями) и определите оптима­ль­ную систему для всех восьми случаев.

4) Проанализируйте полученные результаты.

Отчет о работе

Отчет должен содержать таблицу с исходными данными, промежуточными расчетами и полученными результатами.

Образец отчета показан на Рис. 3‑4.

 

Рис. 3‑4. Пример отчета

Левая нижняя часть excel-листа содержит исходные и данные и ячейки для вспомогательных значений, используемых в выражениях для подсчета нужных значений.

В правой нижней части excel-листа приводятся полученные результаты – вычисленные значения скалярного критерия и номера наилучшей системы.

3.5 Контрольные вопросы

1) Что называется частным показателем качества системы?

2) Что такое обобщенный показатель качества системы?

3) На какие основные классы распадаются критериев оценки сложных систем?

4) Какие элементы образуют множество Парето?

5) Как определяется аддитивный критерий свертки?

6) Из каких основных этапов состоит процедура свертки?

7) Как определяется мультипликативный критерий свертки?

8) В чем заключаются преимущества и недостатки аддитивного и муль­ти­пли­кативного критериев свертки?

Варианты

 

	k1	k2	k3	k4
li	0.25	0.20	0.20	0.35
Kопт	max	max	min	max

 

	k1	k2	k3	k4
li	0.15	0.40	0.20	0.25
Kопт	max	max	min	max

 

	k1	k2	k3	k4
li	0.30	0.30	0.15	0.25
Kопт	min	min	min	max

 

	k1	k2	k3	k4
li	0.10	0.40	0.10	0.35
Kопт	min	max	min	max

 

	k1	k2	k3	k4
li	0.35	0.20	0.10	0.35
Kопт	min	min	min	max

 

	k1	k2	k3	k4
li	0.15	0.40	0.20	0.25
Kопт	max	max	min	max

 

	k1	k2	k3	k4
li	0.20	0.40	0.15	0.25
Kопт	min	max	min	min

 

	k1	k2	k3	k4
li	0.30	0.30	0.15	0.25
Kопт	min	min	min	max

 

	k1	k2	k3	k4
li	0.20	0.40	0.15	0.25
Kопт	min	max	min	min

 

	k1	k2	k3	k4
li	0.50	0.20	0.15	0.15
Kопт	min	max	max	min

 

	k1	k2	k3	k4
li	0.20	0.40	0.15	0.25
Kопт	max	max	min	min

 

	k1	k2	k3	k4
li	0.30	0.30	0.15	0.25
Kопт	min	min	max	max

 

	k1	k2	k3	k4
li	0.10	0.40	0.15	0.35
Kопт	max	min	min	max

 

	k1	k2	k3	k4
li	0.35	0.20	0.10	0.35
Kопт	min	min	min	max

 

	k1	k2	k3	k4
li	0.30	0.30	0.15	0.25
Kопт	min	max	min	max

 

	k1	k2	k3	k4
li	0.25	0.20	0.25	0.30
Kопт	max	min	min	min

 

	k1	k2	k3	k4
li	0.50	0.20	0.15	0.15
Kопт	min	min	max	min

 

	k1	k2	k3	k4
li	0.20	0.40	0.15	0.25
Kопт	max	max	min	min

 

	k1	k2	k3	k4
li	0.35	0.30	0.15	0.20
Kопт	min	min	min	max

 

	k1	k2	k3	k4
li	0.25	0.35	0.20	0.20
Kопт	min	max	min	min

 

	k1	k2	k3	k4
li	0.25	0.25	0.15	0.35
Kопт	min	min	max	max

 

	k1	k2	k3	k4
li	0.15	0.35	0.15	0.35
Kопт	min	max	min	max

 

	k1	k2	k3	k4
li	0.10	0.35	0.20	0.35
Kопт	max	max	min	max

 

	k1	k2	k3	k4
li	0.30	0.30	0.15	0.25
Kопт	max	max	min	min

 

 

4 Сетевое планирование и управление

Цель работы

Изучение детерминированной и вероятностной сетевой моде­ли планирования и управления.

Теоретические сведения

Основные понятия

Сетевое планирование и управление [5] – метод исследования и проек­ти­ро­ва­ния сло­ж­ных систем. Метод позволяет провести анализ и оптимизацию про­цес­сов, состоящих из связанных подсистем или совокупности по­сле­­до­ва­те­ль­ных и взаимосвязанных работ и событий. Основой для анализа и расчетов про­­цес­сов является математическая модель в виде ориен­тированного графа [Рис. 4‑1], на­зы­ва­е­мая сетевой моделью.

Рис. 4‑1 Пример простейшей сетевой модели

Основными элементами сетевой модели являются событие, работа и путь.

Работа - процесс, связанный с затратами времени и ресурсов, и приводящий к достижению опре­де­ле­н­ных результатов. (Работами следует считать также процессы, не требующие расходов ресурса, но только времени).

Ресурсы -материалы, сырье, оборудование, контингент исполнителей, не­об­хо­ди­мые для про­изводства работы, финансовые средства и прочее.

Фиктивная работа отображает логическую связь работ и не требует ра­схода вре­ме­ни и ресурсов (работа (1,3) на Рис. 4‑1). Она только констатирует, что событие (3) не может произойти, пока не све­р­ши­тся событие (1).

В сетевых моделях работы отображаются направленными стрелками, фик­ти­в­ная работа – пунк­ти­ром, рядом с ними изображаются длительности работ t (i,j).

Событие - факт завершения всех предшест­вую­щих работ и готовности к выпол­не­нию всех последующих.

Каждая работа в сети характеризуется:

- начальным событием – (i);

- конечным событием – (j);

Работы кодируются в терминах событий, т.е. каждая из них иден­тифи­ци­ру­ет­ся своими начальным и конечным событиями. Работы с одинаковыми i j не допускаются. В этом случае следует ввести фик­тивные работы, которые обе­с­пе­чивают необхо­димую развязку.

Исходное событие («самое начальное») сети (0) иногда обозначается (I); за­ве­р­шающее событие («са­мое конечное») – (С).

Нумерация событий

Для любой работы сетевой модели:

- номер начального события должен быть меньше номера конечного события (i < j) и

- каждый путь должен проходить по возрастающей последовательности номе­ров событий.

Для нумерации событий используется алгоритм вычеркивания дуг, который также позволяет обна­ру­живать структурные ошибки:

- отыскивается начальное событие (в него не входит ни одна работа), ко­то­рому присваивается но­мер 0.

- зачеркиваются работы, выходящие из него;

- определяются события, не имеющие входящих работ (первый ранг),

- выявленные события нумеруются в произвольном порядке (1, 2 или 2, 1);

- зачеркиваются работы, выходящие из них, определяются события вто­рого ранга;

- по достижении конечного события процесс прекращается.

Критический путь

Путь – последовательность работ в сети, в которой конечное событие любой ра­боты совпадает с на­ча­­льным событием следующей за ней работы.

Путь кодируется в событиях, через которые он проходит, например, путь (3,5,6), иногда он обозна­ча­ет­­ся начальным и конечным событиями пути – L(3,6).

Наибольший интерес представляют собой полные пути (в дальнейшем – про­сто путь), идущие от начального события до конечного события.

Если известны все длительности работ на сетевой модели, то можно опре­де­лить про­должи­тель­ность любого пути T(L) как:

Например, для путей Рис. 4‑1:

- T(L(0,1,4,6))=28;

- T(L(0,1,3,5,6))=30;

- T(L(0,3,5,6))=27;

- T(L(0,2,5,6))=23;

- T(L(0,2,6))=21.

Путь, имеющий наибольшую продолжительность, называется критическим. Lкр, и длительность его обо­з­начается Tкр.

В рассматриваемом примере Lкр=(0, 1, 3, 5, 6), Tкр =30.

Работы, находящиеся на критическом пути, называются критическими. В рассматриваемом случае это работы (0,1), (1,3), (3,5), (5,6).

Критические работы выделяются на сетевой модели жирными или двойными стрелками.

Время выполнения проекта в целом не может быть меньше Tкр, поэтому пер­вая задача при анализе сетевых моделей – выявление Lкр и критических ра­бот и по­иск возможностей по сокра­ще­нию их длите­льно­сти. Нахождение кри­ти­ческого пу­­ти является основной задачей метода критического пути. В методах ана­ли­за сетевой модели используются временные характеристики со­бытий и работ.

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: