 |
Если две пересекающиеся прямые одной плоскости параллельны второй плоскости, то эти плоскости параллельны.
|
|
|
|
Если две пересекающиеся прямые одной плоскости параллельны второй плоскости, то эти плоскости параллельны.
Рассмотрите различные случаи взаимного расположения данных прямых.
15. Воспользуйтесь свойствами параллельного проектирования.
Параллельной проекцией прямой является прямая, а проекцией отрезка — отрезок.
Проекции параллельных прямых — параллельны или совпадают.
Воспользуйтесь свойства параллельных проекций плоских фигур:
Проекцией угла является угол.
Проекцией треугольника является треугольник.
Проекцией параллелограмма является параллелограмм.
Проекцией трапеции является трапеция.
Проекцией п-угольника является п-угольник.
16. Чтобы построить сечение куба, тетраэдра, п-угольной пирамиды и т. п., необходимо построить пересечение каждой грани с секущей плоскостью.
17. Воспользуйтесь признаком перпендикулярности двух плоскостей, определением угла между двумя плоскостями.
Если одна из двух плоскостей проходит через прямую, перпендикулярную второй плоскости, то эти плоскости перпендикулярны.
Углом между пересекающимися плоскостями называется угол между прямыми, образующимися при пересечении данных плоскостей плоскостью, перпендикулярной линии их пересечения.
18. Сравните отрезки, длинами которых измеряются данные величины
19. Воспользуйтесь сечением двугранного угла плоскостью, проходящей через данную точку перпендикулярно его ребру.
20. Вначале укажите в плоскости трапеции, если существует, точку, равноудалённую от всех её вершин или от всех её сторон.
Повышенный уровень Вариант 1
1. Чему равно произведение log32× log43× … log109× log1110?
|
|
|
А. log211. Б. log113. В. log310. Г. log112.
2. Если tgj + ctgj = m, то sinj + cosj при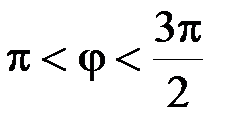 
равно …
А. . Б. . В. . Г. .
3. Первая цифра после запятой в десятичной записи числа 
заключена в интервале…
А. (6; 9). Б. (4; 7). В. (3; 6). Г. (5; 8).
4. Среди участников лыжной гонки число сошедших с дистанции оказалось заключенным между 2, 6% и 2, 7%. Какое минимально возможное число участников гонки?
А. 40. Б. 39. В. 38. Г. 37.
5. Множеством значений функции f(x) = x2 – 2x + sina + 1 не может быть промежуток …
А. [2; +¥ ). Б. 
. В. [–1; +¥ ). Г. [0; +¥ ).
6. График функции 
симметричен относительно …
А. оси у. Б. оси х. В. начала координат. Г. прямой у = 1.
7. Сумма корней уравнения 
, лежащих на промежутке [0; 2p], равна …
А. 2p. Б. p. В. . Г. .
8. Сколько решений имеет система уравнений 
?
А. Ни одного. Б. Два. В. Шесть. Г. Четыре.
9. Найдите все значения параметра а, при которых неравенство x2 – 2x + 2a < 0 не имеет решений.
А. [1; +¥ ). Б. [0; +¥ ). В. (0; 1). Г. (–¥; 1).
10. Сколько существует двузначных чисел в 4 раза больших суммы их цифр?
А. Четыре. Б. Три. В. Два. Г. Одно.
11. Даны две скрещивающиеся прямые а и b. Сколько существует пар взаимно перпендикулярных плоскостей, одна из которых проходит через а, а другая через b?
А. Ни одной. Б. Одна. В. Бесконечно много. Г. Ни одной или одна.
12. Из трех точек, лежащих в горизонтальной плоскости на расстоянии a, b, c от основания телевизионной вышки, эту вышку видно под углами сумма которых равна 90°. Высота вышки равна …
А. 
. Б. 
. В. 
. Г. 
.
13. Через вершину В прямоугольника ABCD со сторонами АВ = 2 и ВС = 5 проведен перпендикуляр ВР к плоскости ABCD. Сравните углы a и β, образованные, соответственно, плоскостями ADP и CDP с плоскостью АВС.
А. a < β. Б. a > β. В. a = β. Г. Сравнить невозможно.
|
|
|
14. Сколько осей симметрии имеет пространственная фигура, состоящая из двух пересекающихся прямых?
А. Ни одной. Б. Одна. В. Две. Г. Три.
15. Ортогональная проекция куба, имеющая наибольшую площадь, является …
А. квадратом. Б. шестиугольником.
В. прямоугольником. Г. пятиугольником.
|
|
|
