 |
Подсказки к заданиям тестов продвинутого уровня
|
|
|
|
Подсказки к заданиям тестов продвинутого уровня
1. Вначале определите знак логарифма, а затем подбором найдите искомые числа.
2. Приведите вначале оба корня к обшему показателю, а затем перемножьте их подкоренные выражения и запишите произведение под знаком корня с тем же показателем. Обратите внимание на связь подкоренных выражений. Применив основное свойство корня, приведите сомножители к одинаковому показателю корня.
Если а ³ 0, то для натуральных п, m и k, п > 1, справедливо равенство 
3. Примените формулы приведения к некоторым парам слагаемых и основное тригонометрическое тождество.
Примените следствия из основного тригонометрического тождества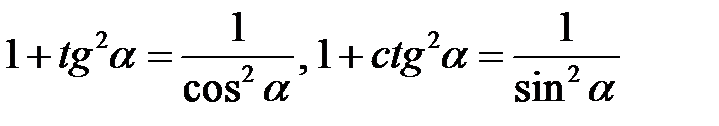 
. Обратите внимание на то, что sina и cosa имеют одинаковые знаки. При необходимости вначале преобразуйте данное выражение.
4. Выразите искомое выражение через данное возведением искомого выражения в квадрат, воспользовавшись тем, что ах× а-х = а0 = 1. Если же дано значение а4х + а-4х, то этот приём повторите дважды.
5. Воспользуйтесь основным логарифмическим тождеством 
и следующими свойствами логарифмов:
Для произвольных положительных а, b, с, a ¹ 1, с ¹ 1 и произвольного действительного р справедливы равенства: 
, 
.
6. Воспользуйтесь тем, что оборот колеса составляет 360° или 2p радиан, и за один оборот колесо проходит путь, равный длине окружности колеса.
7. Можно последовательно находить значение рассматриваемой величины через 1. 2, 3, … единицы времени. Проконтролируйте выдвинутую гипотезу подстановкой нескольких значений t.
8. Воспользуйтесь тем, что область определения функции 
, где а — некоторое число, совпадает с множеством решений неравенства ах ³ 0. Определите знак числового множителя, стоящего под корнем.
|
|
|
9. Воспользуйтесь тем, что график функции y = f(аx + b) = (a > 0) получают из графика функции у = f (х) сжатием его к оси у в а раз при а > 1 и растяжением в раз от оси у при 0 < а < 1), затем параллельным переносом вдоль оси х на | | единиц: в направлении оси х, если < 0 и в противоположном направлении, если > 0. Если а < 0, то применяют ещё симметричное отражение относительно оси у.
10. Воспоьзуйтесь определениями чётной и нечётной функций.
Функция у = f(х) называется чётной, если:
1) её область определения вместе с каждой точкой х содержит и точку –х;
2) для каждого х из области определения функции выполняется равенство:
f(–х) = f(x).
Функция у = f(х) называется нечётной, если:
1) ее область определения вместе с каждой точкой х содержит и точку –х;
2) для каждого х из области определения функции выполняется равенство:
f(–х) = – f(x).
Сравните значения функции в точках х и –х.
11. Обычно уравнение f(x)× g(x) = 0 решают так:
а) находят область опрежеления уоравнения;
б) решают каждое из уравнений совокупности 
;
в) из найденных решений совокупности отбирают те, которые входят в область определения данного уравнения.
12. Сначала найдите зависимость решения от параметра. Далее воспользуйтесь тем, что линейное уравнение ах = b:
а) имеет единственное решение, если а 
б) имеет бесконечное множество решений, если а = b = 0;
в) не имеет решений, если а = 0, b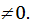 
13. Воспользуйтесь тем, что логарифмическое неравенство 
при
0 < a < 1 равносильно системе неравнств 
а при а > 1 — системе неравенств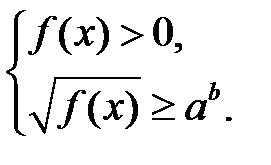 
14. Воспользуйтесь признаком параллельности плоскостей.
|
|
|
