 |
Подсказки к заданиям тестов основного уровня
|
|
|
|
А. [-0, 001; 1000]. Б. .
В. [1000; +¥ ). Г. (0; 1000].
16. Ежегодно зарплата молодого специалиста возрастает на р%. Выразите через р количество лет п, через которое зарплата возрастёт в 5 раз.
А. 
. Б. 
. В. 
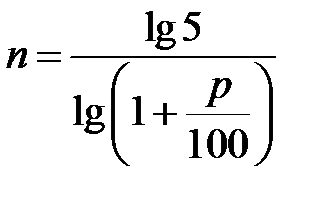. Г.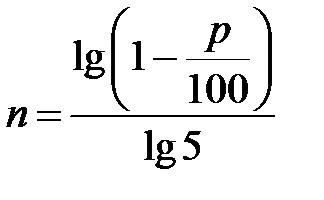 
.
17. Сколько корней имеет уравнение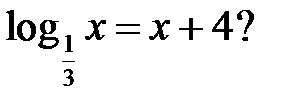 
А. Ни одного. Б. Один. В. Два. Г. Три.
18. Плоскости a и b пересекаются по прямой а, прямая b лежит в плоскости a и не пересекает плоскость b. Как расположены прямые а и b?
А. Скрещиваются. Б. Пересекаются. В. Параллельны.
Г. Могут быть расположены как угодно.
19. Известно, что прямая а параллельна прямой b, а прямая b параллельна плоскости g. Как расположены прямая а и плоскость g?
А. Обязательно параллельны. Б. Могут пересекаться.
В. Прямая а лежит в плоскости g.
Г. Прямая а или параллельна плоскости g, или лежит в ней.
20. Сколько плоскостей можно провести через одну из двух скрещивающихся прямых параллельно другой прямой?
А. Одну. Б. Две. В. Бесконечно много.
Г. Ответ зависит от расположения прямых.
21. Сколько плоскостей, перпендикулярных данной плоскости, проходит через прямую, перпендикулярную к данной плоскости?
А. Одна. Б. Две. В. Три. Г. Бесконечно много.
22. Плоскости правильных треугольников ABC и ABC1 перпендикулярны, АВ = а. Длина СС1 равна …
А. 
. Б. 
. В. 
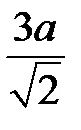. Г. 
.
23. Длина перпендикуляра, проведенного из некоторой точки к плоскости a, равна длине проекции наклонной, проведенной из той же точки, на ту же плоскость. Чему равен угол между наклонной и плоскостью?
А. 30°. Б. 45°. В. 60°. Г.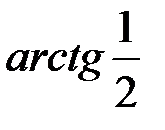 
.
24. Точка М, не лежащая в плоскости равнобедренной трапеции, удалена от всех ее сторон на расстояние 10 см, а от ее плоскости на 8 см. Высота трапеции равна...
|
|
|
А. 6 см. Б. 12 см. В. 
см. Г. 2 
см.
25. Из центра О правильного треугольника ABC восстановлен перпендикуляр OS, который вдвое короче стороны треугольника. Угол между плоскостями SВС и ABC равен...
А. 30°. Б. 45°. В. 60°. Г. .
Подсказки к заданиям тестов основного уровня
1. Обратите внимание на то, что колесо вращается равномерно и что один оборот составляет 360°.
2. Найдите на тригонометрической окружности точку с указанной координатой (или соответствующую данному значению) и определите наименьшее положительное число, соответствующее этой точке. Если существуют и другие числа, соответствующие этой точке, то они отличаются от найденного на 2pп, п Î Z. Координаты найденной точки можно найти, применив соотношения между сторонами и углами в прямоугольном треугольнике.
3. Примените основное тригонометрическое тождество sin2a + cos2a = 1 или следствия из него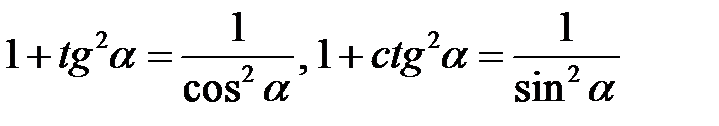 
. По заданному условию, воспользовавшись знаками тригонометрических функций, установите знак искомого значения.
4. Определите знаки заданных чисел, проверьте, нет ли среди них равных нулю.
5. В первую очередь необходимо привести логарифмы к одному основанию, пользуясь формулой 
. Затем воспользуйтесь следующими свойствами логарифмов положительных чисел и определением логарифма.
Для произвольных положительных а, b, с, a ¹ 1 и произвольного действительного р справедливы равенства:
, 
, 
.
6. Используйте формулы приведения: в формуле приведения название функции не меняется, если к аргументу t прибавлять ±pили же ±2p, и меняется (синус на косинус, тангенс на котангенс, косинус на синус, котангенс на тангенс), если прибавлять числа ± или ±. Полученная функция в правой части равенства берется со знаком, совпадающим со знаком значения левой части, если считать, что 0 < t < . При необходимости примените основное тригонометрическое тождество sin2a + cos2a = 1.
|
|
|
Можно воспользоваться геометрическими соображениями — точки тригонометрической окружности, которые соответствуют заданным углам, симметричны относительно оси х, их проекции на одну и ту же ось или противоположны, или равны.
7. Воспользуйтесь тем, что синус острого угла прямоугольного треугольника равен косинусу другого острого угла этого треугольника, а тангенс острого угла прямоугольного треугольника равен котангенсу другого острого угла этого треугольника. Не забудьте и о прямом угле.
8. Воспользуйтесь тем. что множеством значений функций у = sin х и у = cos х является отрезок [–1; 1] и свойствами неравенств. Обратите внимание на то, принимает ли на заданном промежутке sina или cosa все значения из промежутка [–1; 1].
9. Воспользуйтесь тем, что область определения функции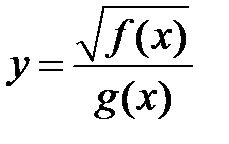 
состоит из тех и только тех значений х, при которых f(x) ³ 0, g(x) ¹ 0.
10. Для нахождения функции, график которой задан, воспользуйтесь правилами преобразования графика функции.
|
|
|
