 |
Повышенный уровень Вариант 2. Повышенный уровень Вариант 2 . А. Б.2p. В.p. Г.
|
|
|
|
Повышенный уровень Вариант 2
1. Чему равно произведение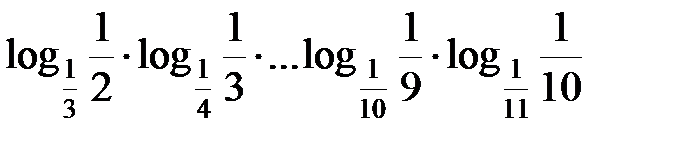 
?
А. log211. Б. log113. В. log310. Г. log112.
2. Если tgj + ctgj = m, то cosj – sinj при 
равно …
А. . Б. . В. . Г. .
3. Первая цифра после запятой в десятичной записи числа 
заключена
в интервале …
А. (1; 4). Б. (2; 5). В. (3; 6). Г. (5; 8).
4. В некотором регионе среди выпускников школ, сдававших ЕГЭ по
определённому предмету число несдавших оказалось заключенным
между 2, 4% и 2, 8%. Какое минимально возможное число выпускников,
сдававших ЕГЭ по этому предмету?
А. 35. Б. 36. В. 39. Г. 41.
5. Множеством значений функции f(x) = x2 + 2x + cosa + 1 не может
быть промежуток …
А. [1; +¥ ). Б. [2; +¥ ). В. [0; +¥ ). Г. [–1; +¥ ).
6. График функции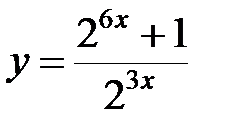 
симметричен относительно …
А. начала координат. Б. оси х. В. оси у. Г. прямой у = 1.
7. Сумма корней уравнения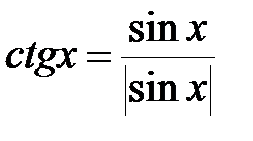 
, лежащих на промежутке [0; 2p],
равна …
А. 2p. Б. p. В. 
. Г. 
.
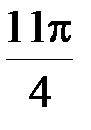8. Сколько решений имеет система уравнений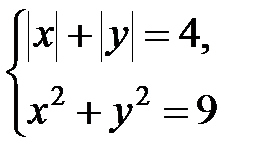 
?
А. Четыре. Б. Восемь. В. Два. Г. Шесть.
9. Найдите все значения параметра b, при которых неравенство
x2 + 2bx + 1 £ 0 не имеет решений.
А. (–¥; 1). Б. (0; 1). В. (–1; 1). Г. (–¥; –1).
10. Сколько в первой сотне чисел, равных сумме их цифр?
А. 12. Б. 11. В. 10. Г. 9.
11. Даны две скрещивающиеся прямые а и b. Сколько существует плоскостей, проходящих через прямую а и перпендикулярных прямой b?
А. Ни одной. Б. Одна. В. Бесконечно много. Г. Ни одной или одна.
12. Из трех точек, лежащих в горизонтальной плоскости на расстоянии
a, b, c от основания телевизионной вышки, эту вышку видно под углами
сумма которых равна 180°. Высота вышки равна …
А. 
. Б. 
. В. 
Г. 
.
13. Через вершину А прямоугольника ABCD со сторонами АВ = 3 и
|
|
|
ВС = 4 проведен перпендикуляр AS к плоскости ABCD. Сравните углы
a и β, образованные, соответственно, плоскостями SBC и SDC
с плоскостью АВС.
А. Сравнить невозможно. Б. a < β. В. a = β. Г. a > β.
14. Сколько осей симметрии имеет пространственная фигура, состоящая
из двух параллельных прямых?
А. Ни одной. Б. Две. В. Три. Г. Бесконечно много.
15. Ортогональная проекция куба, имеющая наименьшую площадь, является …
А. шестиугольником. Б. квадратом.
В. треугольником. Г. пятиугольником.
Повышенный уровень Вариант 3
1. Сравните числа 
и 
.
А. a < b. Б. a = b. В. a > b. Г. Сравнить нельзя.
2. Упростите выражение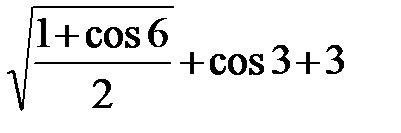 
.
А. 2cos3 + 3. Б. sin3 + cos3 + 3. В. –sin3 + cos3 + 3. Г. 3.
3. Первая цифра после запятой в десятичной записи числа 
заключена в интервале …
А. (3; 6). Б. (6; 9). В. (4; 7). Г. (8; 11).
4. При выборочном контроле партии изделий число бракованных изделий оказалось заключенным между 2, 5% и 2, 6%. Какое минимально возможное число изделий в партии?
А. 38. Б. 40. В. 39. Г. 41.
5. Множеством значений функции y = 4x + cosa – x2 – 4 может быть промежуток …
А. (–¥; 2] Б. (–¥; 1, 5]. В. (1; +¥ ). Г. (–¥; 0, 5).
6. Укажите все значения а, при которых функция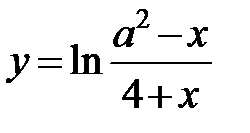 
нечетна.
А. 4. Б. 4; –4. В. 2; –2. Г. Таких значений нет.
7. Сумма корней уравнения 
, лежащих на промежутке [0; 2p], равна…
А. . Б. 2p. В. p. Г. .
8. Сколько решений имеет система уравнений 
?
А. Ни одного. Б. Одно. В. Два. Г. Четыре.
9. Укажите все значения параметра а, при которых неравенство tg2x – 2tgx + 0, 2a < 0 не имеет решений.
А. [0; +¥ ). Б. (–¥; –1]. В. [1; +¥ ). Г. (–¥; 0].
10. Сколько существует двузначных чисел, в 3 раза больших суммы их цифр?
А. Ни одного. Б. Одно. В. Два. Г. Четыре.
11. Даны три попарно скрещивающиеся прямые а, b и с. Сколько существует прямых, пересекающих все эти три прямые?
А. Бесконечно много. Б. Одна. В. Ни одной. Г. Ни одной или одна.
|
|
|
12. Найдите расстояние между диагональю А1С куба АВСDA1B1C1D1 с ребром 8 и прямой, проходящей через середины ребер ВС и В1С1.
А.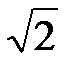 
. Б. 
. В. 4. Г. 
.
13. В кубе АВСDA1B1C1D1 проведено сечение плоскостью A1C1D. Сравните угол a между этой плоскостью и гранью A1B1C1D1 и угол β = Ð A1DC1.
А. a < β. Б. a = β. В. a > β. Г. Сравнить невозможно.
14. Сколько осей симметрии имеет пространственная фигура, состоящая из двух равных правильных четырёхугольных пирамид, вершины которых расположены по разные стороны от общего основания, а боковые ребра не равны ребрам основания?
А. Десять. Б. Шесть. В. Пять. Г. Одну.
15. Длины ребер прямоугольного параллелепипеда равны 1, 2, 3. Чему равно наибольшее значение площади ортогональной проекции этого параллелепипеда на некоторую плоскость?
А. 3, 5. Б. 14. В. 7. Г. 5, 25.
|
|
|
