 |
Лекция 7 (продолжение). Примеры решения на сложное сопротивление
|
|
|
|
Выбрать язык ▼
Главная
Лекция 7 (продолжение). Примеры решения на сложное сопротивление
Расчет стержней при внецентренном сжатии-растяжении
Пример 1.
Чугунный короткий стержень сжимается продольной силой F = 600 кН, приложенной в точке В.
Требуется:
1. Определить положение нейтральной линии;
2. Вычислить наибольшие растягивающие и наибольшие сжимающие напряжения.
Решение.
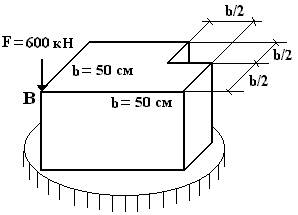
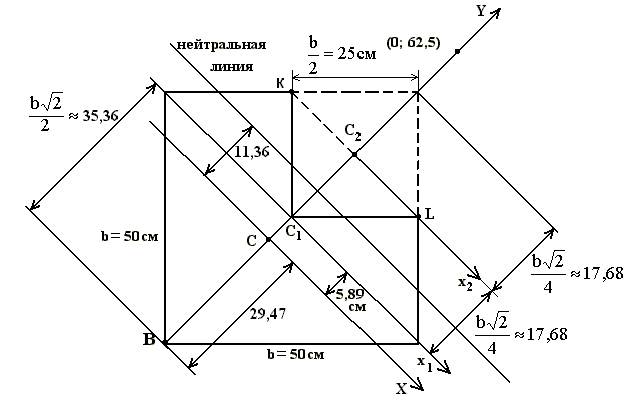
1. Изобразим сечение в масштабе.
2. Определим положение главных центральных осей. Сечение обладает осью симметрии, поэтому ось Y можем показать сразу.
3. Определим положение центра тяжести фигуры (фигура состоит из двух квадратов). Выберем произвольную вспомогательную систему координат.
х1С1Y – вспомогательная система координат;
определим координаты точек С1 и С2 в системе х1С1Y.
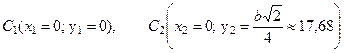
Тогда,
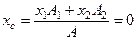
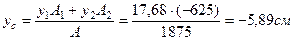
А1, А2 – площадь первого и второго квадрата соответственно.
А = А1 – А2 – площадь всей фигуры.
А1 = b2 = 2500 см2
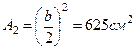
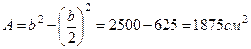
С (хс = 0; ус = -5, 89) – положение центра тяжести во вспомогательной системе координат х1С1Y.
Ось X проводим перпендикулярно оси Y через точку С.
Так как сечение симметричное, то XСY – главная центральная система координат.
4. Определим главные центральные моменты инерции и квадраты главных радиусов сечения.
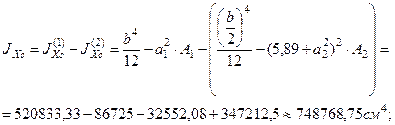
где а1 = 5, 89см – расстояние между осями Х и х1;
а2 = 5, 89 + 17, 68 = 23, 57 – расстояние между осями Х и х2.
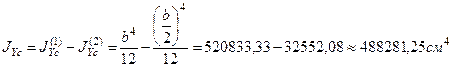
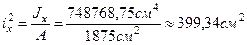
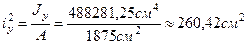
5. Определим координаты точки В (точки приложения силы) в главной центральной системе координат хсСус.
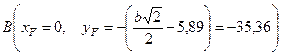
6. Определим положение нейтральной линии.
,
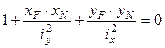где хN, уN – координаты точек нейтральной линии.
В данной задаче
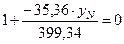
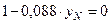
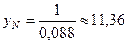
Нейтральная линия проходит через точку (хN=0; уN=11, 36) параллельно оси хс.
|
|
|
7. В данной задаче на стержень действует сжимающая сила, поэтому нормальные напряжения в любой точке поперечного сечения будем определять по формуле
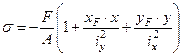
где х, у – это координаты точки, в которой считают напряжения.
8. Наибольшие сжимающие напряжения достигаются в точке В. Эта точка, наиболее удаленная от нейтральной линии в области сжатия.
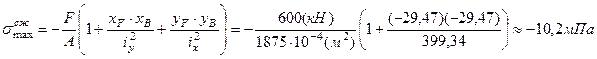
Наибольшее растягивающие напряжения достигаются в точках К и L yK = уL = 23, 57 см.
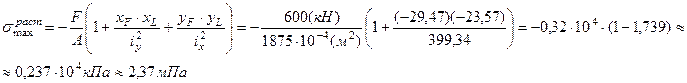
Ответ: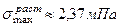 
, 
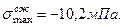
Пример 2.
Построить ядро сечения.
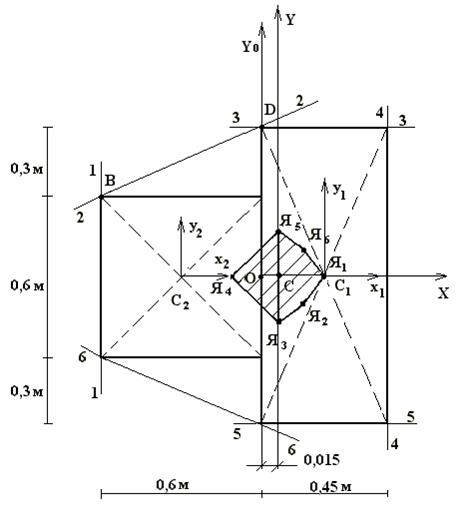
Решение.
1. Определяем тип контура ядра сечения.
2. Определяем число вершин многоугольника, получившегося внутри контура (то есть число предельных касательных к сечению стержня). 6 предельных касательных - 6 вершин.
3. Определяем положение главных центральных осей. Сечение обладает горизонтальной осью симметрии, поэтому ось «Х» можем показать сразу. ХОY0 – вспомогательная система координат (ось «Y0» проводим произвольно).
Сечение состоит из двух простых фигур (прямоугольника и квадрата). Определим координаты центров тяжести С1 и С2 в произвольной системе координат ХОY0.
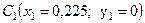- центр тяжести прямоугольника.
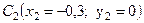- центр тяжести квадрата.
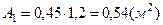- площадь прямоугольника.
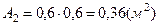- площадь квадрата.
.
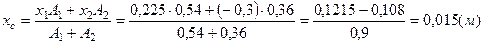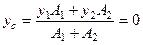(так как С1 и С2 лежат на оси).
Центр тяжести всего сечения в системе координат ХОY0 имеет координаты С(0, 015; 0). (Покажем на чертеже).
Ось Y проводим перпендикулярно оси Y0 через центр тяжести С.
Так как сечение симметричное, то ось симметрии и ось ей перпендикулярная, проходящая через центр тяжести образуют главную центральную систему координат.
X, Y – главные центральные оси сечения.
4. Определяем геометрические характеристики сечения относительно главных центральных осей.
Вычисляем главные центральные моменты инерции Jx и Jy.
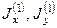- главные центральные моменты инерции прямоугольника.
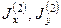- главные центральные моменты инерции квадрата.
|
|
|
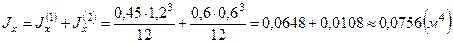
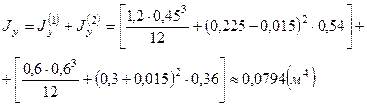
(здесь использовали формулы для определения моментов инерции относительно параллельных осей. Осевые моменты инерции плоского сечения относительно произвольных осей х1 и у1, параллельных центральным осям х и у, определяют по формулам
;
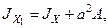
где а, b – расстояния между осями х и х1, у и у1, А – площадь поперечного сечения. принимается, что х, у – центральные оси, то есть оси, проходящие через центр тяжести С плоского сечения).
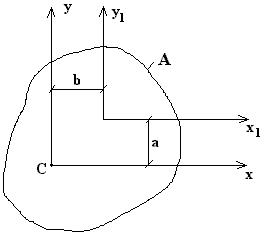
Вычислим квадраты главных радиусов инерции
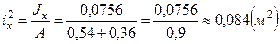
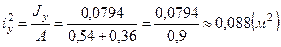
5. Определяем вершины ядра сечения.
Пусть известно положение нейтральной линии. Требуется определить координаты точки приложения силы.
1. Рассмотрим положение нейтральной линии 1 – 1.
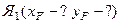
Используем свойство нейтральной линии. Так как нейтральная линия 1–1 проходит параллельно оси Y, то точка приложения силы Я1 находится на оси X, то есть уF =0.
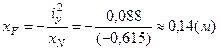
хN – абсцисса точки нейтральной линии 1 – 1 (расстояние от точки С до нейтральной линии 1 – 1).
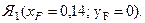
2. Рассмотрим положение нейтральной линии 2 – 2.
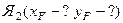
Возьмем две точки нейтральной линии 2 – 2 (лучше выбирать точки, где легко можно подсчитать координаты)
В(-0, 615; 0, 3) и D(-0, 015; 0, 6)
Подставим координаты точек В и D в уравнение нейтральной линии.
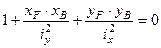(1)
(2)
Решим систему уравнений (1) – (2)
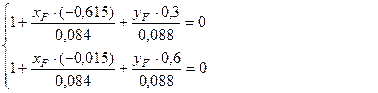
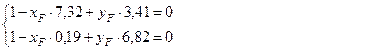
Из первого уравнения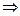 
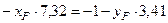
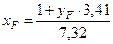
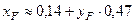(3)
Подставим (3) в (2)
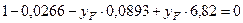
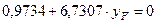
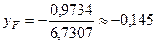
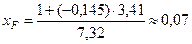
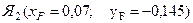
3. Рассмотрим положение нейтральной линии 3 – 3.
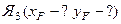
Используем свойство нейтральной линии. Так как нейтральная линия 3 – 3 проходит параллельно оси X, то точка приложения силы Я3 находится на оси Y, то есть хF =0.
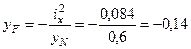
уN – ордината точки нейтральной линии 3 – 3 (расстояние от точки С до нейтральной линии 3 – 3).
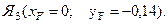
4. Рассмотрим положение нейтральной линии 4 – 4.
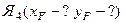
Используем свойство нейтральной линии. Так как нейтральная линия 4 – 4 проходит параллельно оси Y, то точка приложения силы Я4 находится на оси X, то есть уF = 0.
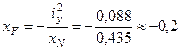
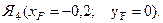
5. Далее воспользуемся симметрией сечения и достроим точки Я5 и Я6 симметрично точкам Я3 и Я2.
|
|
|
