 |
Рис.1 Рис.2. Пример 5.
|
|
|
|
Рис. 1 Рис. 2
Найденные координаты рекомендуем проверить, измерив эти координаты на рисунке сечения, выполненном в большом масштабе.
Для определения положения опасных точек построим нейтральную линию, используя формулы 
; 
. Радиусы инерции 
, 
найдены ранее.
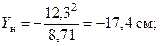
Отложим эти отрезки вдоль главных осей и проведем через полученные точки нейтральную линию 
(см. рис. 3).
Рис. 3
Опасными точками, т. е. точками, наиболее удаленными от нейтральной оси, будут точки 1 и 3 (см. рис. 3). В точке 1 действует наибольшее растягивающее напряжение. Запишем условие прочности в этой точке, используя формулу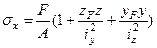 
:
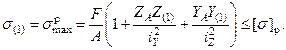
Подставим в условие прочности координаты опасной точки 1 в главных осях, вычислив их по формулам
или измерив на рисунке, выполненном в масштабе, 
Тогда из условия прочности в точке 1 можно найти допускаемое значение нагрузки:
.
Для найденного значения допускаемой нагрузки необходимо убедиться, что условие прочности выполняется и в точке 3, которая дальше удалена от нейтральной линии и в которой д ействует сжимающее напряжение. Для определения напряжения в точке 3 подставим в формулу 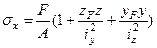координаты этой точки 
.
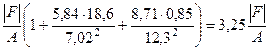Это напряжение не должно превосходить 
. Если условие прочности в точке с максимальными сжимающими напряжениями выполняться не будет, надо найти значение допускаемой нагрузки заново из условия прочности в этой точке.
|
|
|
В заключение построим ядро сечения. Поместим полюсы во внешние угловые точки сечения, т. е. в точки 1, 2, 3, 4, 5 (см. рис. 3). Точка 4, находящаяся на контуре квадранта круга, получена следующим образом. Отсекая внутреннюю угловую точку 
, проводим линию, касательную к контуру сечения (пунктир на рис. 3). Точка 4 является точкой касания этой линией квадранта круга. Последовательно находим положение нейтральных линий, соответствующих полюсам в указанных точках, находя отрезки, отсекаемые нейтральными линиями на осях 
, 
, по формулам ; . Например, если полюс находится в точке 1, то, подставляя в ; координаты точки 1 ( 
), найдем
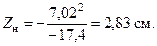
Поскольку 
существенно больше 
, то это значит, что нейтральная линия 1–1 практически параллельна оси . Отрезок откладываем в масштабе вдоль оси и проводим прямую 1–1, параллельную оси (см. рис. 3). Аналогично строим нейтральные линии, соответствующие полюсам, расположенным в других точках. Ядро сечения (заштрихованная область) показано на рис. 3. Отметим, что контур ядра сечения между нейтральными линиями 4–4 и 5–5 очерчен по кривой, т. к. переход полюса из точки 4 в точку 5 происходит не по прямой линии. На рис. 3 показан также эллипс инерции сечения, построенный ранее.
Пример 5.
На брус заданного поперечного сечения в точке D верхнего торца действует продольная сжимающая сила Р=300 кН (см. рис. ). Требуется найти положение нулевой линии, определить наибольшие (растягивающие и сжимающие) напряжения и построить ядро сечения.
Решение:
1. Нахождение положения главных центральных осей инерции и определение площади поперечного сечения
Так как поперечное сечение бруса (рис. 1) имеет две оси симметрии, а они всегда проходят через центр тяжести сечения и являются главными, то главные центральные оси сечения хс и ус будут совпадать с этими осями симметрии.
Центр тяжести сечения С в этом случае определять не надо, так как он совпадает с геометрическим центром сечения.
|
|
|
Площадь поперечного сечения бруса равна:
2. Определение главных центральных моментов инерции и главных радиусов инерции
Моменты инерции определяем по формулам:
Вычисляем квадраты главных радиусов инерции:
3. Определение положения нулевой линии
Отрезки, отсекаемые нулевой линией на главных центральных осях инерции, определяем по формулам:
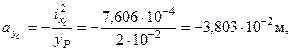
где хр=2, 3 см и ур=2 см – координаты точки приложения силы Р (точка Р рис. 11). Отложив отрезки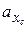 
и 
соответственно на осях хс и ус и проводя через их концы прямую, получим нулевую линию сечения, на которой нормальные напряжения равны нулю ( 
). На рис. 1 эта линия обозначена n-n.
4. Определение наибольших сжимающих и растягивающих напряжений и построение эпюры напряжений
Точка D , координаты которой хD=5, 25 см и уD=5 см, наиболее удалена от нулевой линии в сжатой зоне сечения, поэтому наибольшие сжимающие напряжения возникают в ней и определяются по формуле
Наибольшие растягивающие напряжения возникают в точке К, имеющей координаты хк= ‑ 5, 25 см, ук= ‑ 5 см.
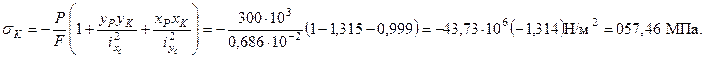
По полученным значениям 
и 
строим эпюру нормальных напряжений (см. рис. 11).
5. Построение ядра сечения
Для построения ядра сечения, учитывая, что сечение симметричное, рассмотрим два положения касательной к контуру сечения I-I и II-II(см. рис. 1).
Отрезки, отсекаемые касательной I-I на осях координат, равны: 
Координаты граничной точки 1 ядра сечения определяются по формулам:
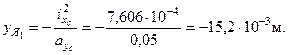
Касательная II-II отсекает отрезки 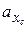=5, 25 см, =¥.
Координаты граничной точки 2:
Координаты граничных точек второй половины ядра сечения можно не определять, так как сечение бруса симметричное. Учитывая это для касательных III-III и IV-IV, координаты граничных точек 3 и 4 будут:
= 0; 
= 15, 2× 10-3 м;
= 23, 0× 10-3 м 
= 0.
Соединив последовательно точки 1, 2, 3 и 4 прямыми получим ядро сечения (рис. 1).
|
|
|
