Пример 13.. Эксцентриситеты силы F  будут равны:

Пример 13.

Построить эпюру нормальных напряжений и определить положение нейтральной линии в прямоугольном поперечном сечении короткого столба, нагруженного вертикальной сосредоточенной силой F, приложенной так, как показано на рис. 1.

Решение.

Эксцентриситеты силы F  будут равны:

Произведя приведение силы к центру, получим

Схема загружения поперечного сечения показана на рис. 2. Нормальные напряжения в угловых точках 1, 2, 3 и 4 (рис. 3), для которых y = y_max и z = z_max, подсчитывают по формуле

причем знаки слагаемых устанавливают в зависимости от того, растяжение или сжатие вызывает в данной точке соответствующий силовой фактор:

   

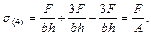
Эпюра напряжений в поперечном сечении изображена на рис. 3.

Для определения положения нейтральной линии воспользуемся формулами :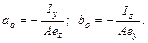

 

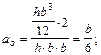
Нейтральная линия показана на рис. 4. Она отсекает отрезки в четвертой четверти координатной системы, показанной на рис. 4.

 

Пример 14.

На рисунке изображено поперечное сечение бруса и показаны центры тяжести четырех простых элементов, составляющих это поперечное сечение. Требуется построить ядро сечения для заданного поперечного сечения.

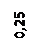
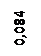
Решение.

Найдем положение центра тяжести всего поперечного сечения. Главная ось у совпадает с осью симметрии сечения. Вычислим площади четырех простых элементов:

А₁ = 0, 6·1, 4/2 = 0, 42 м²;  А₂ = 0, 5·1, 4 = 0, 7 м²;  А₃ = 0, 8·0, 6 = 0, 48 м²; А₄ = 0, 3²/2 = 0, 1413 м².

Площадь всего поперечного сечения будет А = А₁+А₂+А₃+А₄ = 1, 74 м².

Положение главной оси z относительно случайной оси z^/ находим по формуле :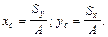

Определим главные моменты инерции относительно осей у и z:

Вычисляем квадраты радиусов инерции поперечного сечения:

;

Нейтральная линия проходит через точки с координатами z = 0, у = b_о и z = а_о, у = 0, которые можно вычислить при помощи формул:

                                   (а)

Если внешняя сила приложена в пределах ядра сечения, то во всем сечении будут нормальные напряжения одного знака. Предположим, что нулевая линия проходит через точки 1 и 2 поперечного сечения, следовательно, b_o = 1, 016 м;  = 0, 7/0, 6; а_о = b_o = 1, 016·0, 7/0, 6 = 1, 185 м.

Из формул (а) находим эксцентриситеты точки приложения сосредоточенной силы

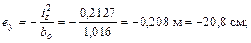
Откладываем эти координаты на рисунке и находим точку О_1-2. Таким образом, если приложить силу в точке О_1-2, то нулевая линия будет проходить через сторону 1 – 2 поперечного сечения. Следовательно, во всем сечении будут нормальные напряжения одного знака.

Теперь предположим, что нулевая линия проходит через точки 2 и 3 поперечного сечения. В этом случае а_о = 0, 7 м; b_o = 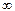, а формулы (а) дают

По этим координатам строим точку О_2-3 (см. рис. ).

Далее предположим, что нулевая линия проходит через точки 3 и 4, причем в точке 4 она является касательной линией к круговому контуру поперечного сечения. Значения а_о и b_o в этом случае можно вычислить теоретически, но это будет довольно сложной операцией, поэтому ограничимся непосредственным измерением а_о и b_o на рисунке, т. е. определим их графически: а_о = 0, 74 м, а b_o = –1, 62 м. Тогда

По этим координатам строим точку О_3-4.

Проводим нулевую линию через точку 5 параллельно оси z, тогда a_o = 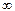, b_o = –y_C = –1, 184 м. По формулам (а) находим координаты точки О₅, где по предположению должна быть приложена сила внецентренного сжатия или растяжения,

Наконец, проводим нулевую линию через точку 1 параллельно оси z. В этом случае b_o = 1, 016 м; а_о = 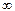. Точка О₁ – точка приложения силы – будет иметь координаты:

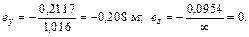
Точки О₁, О_1-2, О_2-3, О_3-4 соединяем прямыми линиями, а точки О_3-4 и О₅ – выпуклой кривой линией. Учитывая симметрию поперечного сечения, продолжаем построения дальше. Внутренняя область, ограниченная построенной линией, будет являться ядром заданного поперечного сечения.

 

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: