 |
Пример 10. Решение. 2. Вычислить наибольшие сжимающие и растягивающие напряжения и построить эпюру напряжений. Дать заключение о прочности колонны.
|
|
|
|
Пример 10.
Короткая колонна, поперечное сечение которой изображено на рис. 1, сжимается продольной силой F=200 кН, приложенной в точке К. Размеры сечения а=40 см, b=16 см. Расчетное сопротивление материала на растяжение Rt = 3 МПа, на сжатие Rс = 30 МПа.
Требуется:
1. Найти положение нулевой линии.
2. Вычислить наибольшие сжимающие и растягивающие напряжения и построить эпюру напряжений. Дать заключение о прочности колонны.
3. Определить расчетную несущую способность (расчетную нагрузку) Fmax при заданных размерах сечения.
4. Построить ядро сечения.
Рис. 1
Решение.
1. Определение координат центра тяжести сечения.
Поперечное сечение колонны имеет ось симметрии Хс, следовательно центр тяжести лежит на этой оси и для отыскания координаты хс относительно вспомогательной оси Yo (см. рис. 1) сложное сечение разбиваем на три прямоугольника
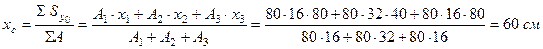
2. Геометрические характеристики сечения.
Для вычисления главных центральных моментов инерции воспользуемся зависимостью между моментами инерции при параллельном переносе осей.
,
Определяем квадраты радиусов инерции
Координаты точки приложения силы F
3. Положение нулевой линии
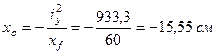
По найденным отрезкам, отсекаемым на осях координат проводим нулевую линию (см. рис. 2).
4. Определение наибольших сжимающих и растягивающих напряжений. Эпюра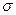 
.
Наиболее удаленные от нулевой линии точки: В (-60; 16) и D (60; -32). Напряжения в этих опасных точках с координатами хdan, уdan не должны превосходить соответствующего расчетного сопротивления
.
Растягивающее напряжение
.
Сжимающее напряжение
|
|
|
.
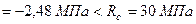Прочность колонны обеспечена.
По результатам расчета напряжений 
и 
на рис. 2 построена эпюра .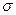
5. Вычисление расчетной несущей способности колонны Fmax.
Поскольку при заданном значении сжимающей силы прочность материала колонны существенно недоиспользована, найдем максимальное значение внешней нагрузки, приравнивая наибольшие напряжения st и sc расчётным сопротивлениям.
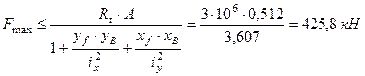
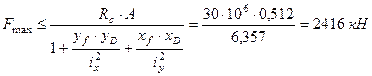
Окончательно выбираем меньше значение Fmax=425, 8 кН, обеспечивающее прочность как растянутой, так и сжатой зон сечения.
Рис. 2
6. Построение ядра сечения.
Чтобы получить очертание ядра сечения, необходимо рассмотреть все возможные положения касательных к контуру сечения и, предполагая, что эти касательные являются нулевыми линиями, вычислить координаты граничных точек ядра относительно главных центральных осей сечения. Соединяя затем эти точки, получим очертание ядра сечения.
Касательная 1-1: yo = 32 см,
.
Касательная 2-2: 
, 
.
Касательная 3-3: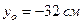 
, 
.
Касательная 4-4: 
; 
;
; 
;
; 
;
;
.
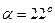Касательная 5-5: 
; 
.
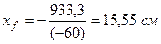Касательная 6-6: 
; 
;
; 
.
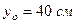Пример 11.
В точке P колонны прямоугольного сечения приложена сжимающая сила P (см. рис. ). Определить максимальное и минимальное нормальные напряжения.
Решение.
Нормальное напряжение при внецентренном сжатии определяем по формуле:
В нашей задаче 
Момент инерции 
, площадь 
,
Следовательно 
На нейтральной линии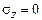 
. Поэтому ее уравнение
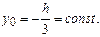
Наиболее удаленными точками от нейтральной оси являются точки A и B:
в точке A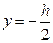 
и
в точке B 
и
Если материал сопротивляется растяжению и сжатию различно, то следует составить два уравнения прочности:
Пример 12.
Найти допускаемую нагрузку для бруса, показанного на рисунке, если расчетные сопротивления материала бруса на растяжение и сжатие равны Radm, t = 20 МПа; Radm, с = 100 МПа.
|
|
|
Решение. Запишем условие прочности для наиболее напряженных точек любого сечения бруса, так как все сечения равноопасны:
Перепишем эти условия, учитывая, что
и 
, тогда
и 
Отсюда определяем значения допустимых нагрузок:
Окончательно в качестве допустимой внешней нагрузки принимаем Fadm = 64кН.
|
|
|
