 |
Пример 8. Решение. 2) найти допускаемую нагрузку F при заданных размерах сечения и допускаемых напряжениях для чугуна на сжатие и на растяжение
|
|
|
|
Пример 8.
Чугунный короткий стержень прямоугольного поперечного сечения, изображенный на рисунке, сжимается продольной силой F, приложенной в точке А.
Требуется:
1) вычислить наибольшее растягивающее и наибольшее сжимающее напряжения в поперечном сечении, выразив величины этих напряжений через F и размеры сечения;
2) найти допускаемую нагрузку F при заданных размерах сечения и допускаемых напряжениях для чугуна на сжатие 
и на растяжение 
.
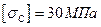Решение.
Определим положение нулевой линии. Для этого воспользуемся формулами
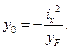
Координаты точки приложения силы (точки А) будут следующими:
Квадраты радиусов инерции определим по формулам:
Определяем отрезки, которые нулевая линия отсекает на осях х и у.
Откладываем на оси х – х0, а на оси у – у0 и проводим через полученные точки нулевую линию n – n (см. рис. ). Видим, что наиболее удаленные точки сечения - это точка А в сжатой области и точка В в растянутой области. Координаты этих точек следующие: А (0, 04; 0, 06), В (–0, 04; –0, 06). Определим величину напряжения в этих точках, выразив их через силу F:
Напряжение в точке А не должно превышать допускаемое напряжение на сжатие 
, а напряжение в точке В не должно превышать допускаемое напряжение на растяжение 
, т. е. должно выполняться условие
, 
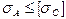или
, 
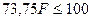Из первого выражения величина F
Принимается нагрузка наименьшая из двух найденных, т. е. 
= 567кн.
Пример 9.
Короткий чугунный стержень с поперечным сечением, изображенным на рис. а, сжимается продольной силой P, приложенной в точке A. Определить наибольшее растягивающее и наибольшее сжимающее напряжения в поперечном сечении стержня, выразив их через силу P и размеры сечения 
см, 
см. Найти допускаемую нагрузку 
при заданных допускаемых напряжениях для материала на сжатие 
кН/см2 и на растяжение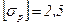 
кН/см2.
|
|
|
Решение.
Действующая на стержень сила P помимо сжатия осуществляет изгиб стержня относительно главных центральных осей x и y. Изгибающие моменты соответственно равны:
,
где 
см и 
см – координаты точки приложения силы P (координаты точки A).
Нормальные напряжения в некоторой точке с координатами x и y любого поперечного сечения стержня определяются по формуле
,
где F – площадь, а 
и 
– радиусы инерции поперечного сечения.
1. Определяем геометрические характеристики поперечного сечения стержня.
Площадь поперечного сечения стержня равна:
.
Главные центральные моменты инерции определяем следующим образом.
Вычисляя момент инерции всего сечения относительно оси x, разобьем всю фигуру на один прямоугольник с шириной 
и высотой 
и два прямоугольника с шириной 
и высотой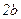 
, чтобы ось x была для всех этих трех фигур центральной. Тогда
.
Для вычисления момента инерции всего сечения относительно оси y разобьем всю фигуру несколько иначе: один прямоугольник с шириной 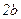и высотой 
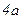и два прямоугольника с шириной 
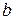и высотой , чтобы теперь уже ось y была для всех этих трех фигур центральной. Получим
.
Квадраты радиусов инерции равны:
; 
.
2. Определяем положение нулевой линии.
Отрезки 
и 
, отсекаемые нулевой линией от осей координат, равны:
см; 
см.
Показываем нулевую линию N – N на рис. б. Нулевая линия делит поперечное сечение на две области, одна из которых испытывает растяжение, а другая – сжатие. На рисунке 1, б растянутая область поперечного сечения стержня нами заштрихована.
3. Вычисляем наибольшее растягивающее напряжение.
Оно возникает в точках 6 и 7, то есть в точках, наиболее удаленных от нулевой линии. Значение этого напряжения, вычисленное, например, для точки 6 равно:
|
|
|
.
4. Вычисляем наибольшее сжимающее напряжение.
Оно возникает в точках 2 и 3, также наиболее удаленных от нулевой линии. Значение этого напряжения, вычисленное, например, для точки 2, равно:
.
5. Определяем допускаемую нагрузку из условия прочности на растяжение:
кН/см2; 
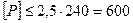кН.
6. Определяем допускаемую нагрузку из условия прочности на сжатие:
кН/см2; 
кН.
7. Допускаемая нагрузка равна меньшему из двух найденных в п. 6 и 7 значений:
кН.
|
|
|
