 |
Пример 6. Решение. Так как оси X и Y являются осями симметрии, то они главные центральные оси. Наиболее опасными точками будут точки, в которых возникают максимальные нормальные напряжения, а это точки, наиболее удаленные от нулевой линии
|
|
|
|
Пример 6.
В сечении, указанном на рисунке и принадлежащем внецентренно сжатой колонне, определить наиболее опасные точки и напряжения в них. Сжимающая сила F = 200 кН = 20 т приложена в точке A.
Решение.
Так как оси X и Y являются осями симметрии, то они главные центральные оси.
Наиболее опасными точками будут точки, в которых возникают максимальные нормальные напряжения, а это точки, наиболее удаленные от нулевой линии. Следовательно, нам необходимо сначала определить положение нулевой линии. Записываем уравнение нулевой линии.
В нашем случае координаты точки приложения силы следующие (см. рис. ):
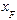= – 90 мм = – 0, 09 м;
= – 60 мм = – 0, 06 м.
Квадраты радиусов инерции 
и 
определяются так:
, 
,
здесь 
и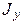 
- осевые моменты инерции относительно главных центральных осей X и Y.
Определение осевых моментов инерции. Для нашего сечения будем иметь:
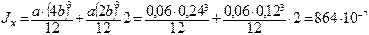м4;
м4.
Площадь всего сечения будет равна:
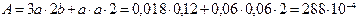м2,
и тогда квадраты радиусов инерции:
м2;
м2.
По формулам определим отрезки, которые нулевая линия отсекает на осях X и Y:
м;
м.
Отложим эти отрезки на координатных осях, получим точки, в которых нулевая линия пересекает координатные оси. Через эти точки проводим прямую (см. рис. ). Видим, что наиболее удаленные точки - это точка B в зоне отрицательных напряжений и точка D в зоне положительных напряжений.
Определим напряжения в этих точках:
;
На основании чертежа (см. рис. ) получим:
= – 0, 12 м; 
= – 0, 03 м.
Тогда
= –5, 39× 104 кН/м2 = – 53, 9 МПа.
;
= 0, 12 м;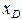 
= 0, 03 м.
= 1, 86× 104 кН/м2 = 18, 6 МПа.
Пример 7.
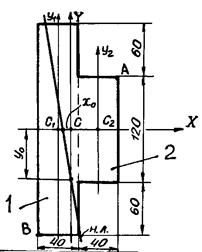
Чугунный короткий стержень, поперечное сечение которого изображено на рисунке, сжимается продольной силой F, приложенной в точке А.
|
|
|
Требуется:
1) вычислить наибольшее растягивающее и наибольшее сжимающее напряжения в поперечном сечении, выразив величины этих напряжений через F и размеры сечения; а = 40 мм, b = 60 мм;
2) найти допускаемую нагрузку F при заданных размерах сечения и допускаемых напряжениях для чугуна на сжатие 
= 100 МПа и на растяжение 
= 30 МПа.
Решение.
Выше указывалось, что геометрические характеристики в расчетных формулах берутся относительно главных центральных осей, поэтому определим центр тяжести сечения. Ось X является осью симметрии, и следовательно, она проходит через центр тяжести, поэтому нам достаточно найти его местоположение на этой оси. Разобьем сечение на два составных (1 и 2) и выберем вспомогательные оси 
. Запишем координаты центров тяжести С1 и С2 в этих осях.
Будем иметь С1 (0, 0); С2(0, 04; 0), тогда:
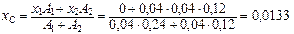м;
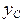= 0.
Итак, в осях xy1 центр тяжести всего сечения имеет координаты С (0, 0133; 0). Проводим через центр тяжести сечения ось Y, перпендикулярную оси X. Оси X и Y и будут главными центральными осями сечения.
Определим положение нулевой линии.
, 
.
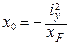Координаты точки приложения силы (точки А) будут следующие: 
=(0, 02–0, 0133)+0, 04 =0, 0467 м; 
= 0, 06 м;
Квадраты радиусов инерции определим по формулам:
, 
.
м4,
м4,
где 
= 0, 0133 м;
м2.
м2, 
м2;
и получим отрезки, отсекаемые нейтральной осью на главных осях инерции X и Y соответственно:
Откладываем 
на оси X, а 
на оси Y и проводим через полученные точки нулевую линию (см. рис. ). Видим, что наиболее удаленные точки сечения от нулевой линии - это точка А в сжатой зоне и точка В в растянутой зоне. Координаты этих точек следующие: А (0, 0467; 0, 06); В (– 0, 0333; –0, 12). Определим напряжения в этих точках, выразив их через F.
Напряжение в точке А не должно превышать допускаемое напряжение на сжатие 
, а напряжение в точке В не должно превышать допускаемое напряжение на растяжение 
, т. е. должны выполняться условия:
|
|
|
, 
,
или
(а),
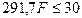(б).
Из (а): 
из (б): 
Чтобы одновременно удовлетворить условие прочности и в растянутой, и в сжатой зонах колонны, мы должны взять в качестве допускаемой нагрузки меньшую из двух полученных, т. е. 
= 103 кН.
|
|
|
