 |
Пример 3. Рис.1 Рис.2. Решение. 2) построить ядро сечения.
|
|
|
|
Пример 3.
Жесткий стержень загружен двумя силами – растягивающей и сжимающей (рис. 1). Стержень выполнен из хрупкого материала с характеристиками 
и 
. Сечение стержня симметрично и имеет форму и размеры, соответствующие рис. 2.
Требуется:
1) найти допускаемую нагрузку на стержень из условия прочности, если отношение сжимающей и растягивающей сил 
2) построить ядро сечения.
Рис. 1 Рис. 2
Решение.
Положение главных центральных осей инерции и моменты инерции относительно этих осей заданного сечения найдены ранее (см. раздел «Геометрические характеристики плоских сечений»). Найдем внутренние усилия в произвольном сечении стержня:
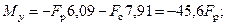
Для определения положения опасных точек построим нейтральную линию. Уравнение нейтральной линии 
в данной задаче имеет вид
Или
.
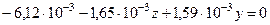Отсюда найдем отрезки, отсекаемые нейтральной линией на осях 
и 
. Если 
, то
и, если 
, то
Нейтральная линия показана на рис. 3.
Рис. 3
Проведем касательные к контуру сечения, параллельные нейтральной линии. Опасными являются точки 1 и 1¢ (см. рис. 3), наиболее отдаленные от нейтральной линии. Для хрупкого материала более опасной является точка с максимальными растягивающими напряжениями, т. е. точка 1. Найдем напряжение в этой точке, подставляя в формулу 
координаты точки 1:
Условие прочности в точке 1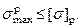 
Или
Отсюда можно найти допускаемое значение нагрузки (не забывайте правильно подставлять единицы измерения. Множитель перед Fp в данном примере имеет размерность см-2).
|
|
|
В заключение необходимо убедиться в том, что и в точке 1¢, которая в данном примере дальше удалена от нейтральной оси, чем точка 1, и в которой действуют сжимающие напряжения, условие прочности тоже выполняется, т. е.
Теперь построим ядро сечения. Поместим полюсы во внешних угловых точках сечения. Учитывая симметрию сечения, достаточно расположить полюсы в трех точках: 1, 2 и 3 (см. рис. 3). Подставляя в формулы 
; 
координаты полюсов, найдем отрезки, отсекаемые нейтральными линиями на осях и . Если полюс находится в точке 1, то его координаты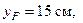 
и
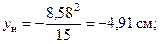
Нейтральная линия 1–1, соответствующая полюсу в точке 1 показана на рис. 3. Аналогично строим нейтральные линии 2–2 и 3–3, соответствующие полюсам 2 и 3. При построении нейтральной линии следите за тем, чтобы она проходила в квадранте, противоположном тому, в котором находится полюс. Область, заштрихованная на рис. 3, является ядром сечения. Для контроля на рис. 3 показан эллипс инерции. Ядро сечения должно находиться внутри эллипса инерции, нигде не пересекая его.
Пример 4.
Стержень несимметричного сечения сжимается силой, приложенной в точке А (рис. 1). Поперечное сечение имеет форму и размеры, показанные на рис. 2. Материал стержня – хрупкий.
Требуется:
1) найти допускаемую нагрузку, удовлетворяющую условию прочности;
2) построить ядро сечения.
Решение.
Прежде всего, надо определить моменты и радиусы инерции поперечного сечения относительно главных центральных осей. Эта часть решения задачи приведена в разделе «Геометрические характеристики плоских сечений». На рис. 1 показаны главные центральные оси инерции сечения 
, 
, положение которых найдено ранее. В системе центральных осей Y, Z (рис. 2) координаты точки приложения силы А 
, 
. Вычислим координаты точки А в системе главных центральных осей по формулам
|
|
|
.
|
|
|
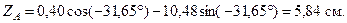
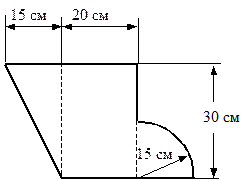
