 |
Подсказки к заданиям базового уровня
|
|
|
|
Подсказки к заданиям базового уровня
1. В записи натурального числа цифры разбивают на группы справа налево по три цифры в каждой группе. Каждую из этих групп называют классом, а расположены они справа налево в таком порядке: класс единиц, класс тысяч, класс миллионов, класс миллиардов, класс триллионов и т. д. Каждый класс имеет три разряда: разряд единиц, разряд десятков, разряд сотен.
Например, число восемь миллионов одиннадцать тысяч двести записывается так:
1) записали класс миллионов;
2) затем класс тысяч, обрптите внимание на то, что в этом классе нет разряда сотен;
3) наконец, класс единиц.
Чтобы прочитать многозначное число, его мысленно разбивают на классы, начиная с клпсса единиц. Числа каждого класса читают, начиная слева, как трёхзначное, двузначное или однозначное число, но при этом добавляют название класса.
Например, число 308 023 105 432 читают так: триста восемь миллиардов 23 миллиона сто пять тысяч четыреста тридцать два.
2. Сложение и вычитание многозначных чисел выполняются поразрядно. Если при вычитании число какого-то разряда уменьшаемого меньше соответствующего числа вычитаемого, то берём единицу высшего разряда. Вычитание и сложение начинаются с единиц.
Например,
3. Натуральные числа складываются по разрядам. При этом нужно учитывать, что каждые 10 единиц любого разряда дают одну единицу более высокого (следующего за ним) разряда. При записи «столбиком нужно внимательно следить за тем, чтобы одноимённые разряды были точно подписаны друг под дру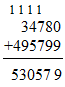 
гом.
Например,
|
|
|
4. Воспользуйтесь тем, что:
если некоторое значение а уменьшилось на с, то остаток находится вычитанием: а – с;
если при уменьшении значения а на некоторое значение получили в остатке с, то значение а уменьшали на а – с;
если в двух совокупностях а единиц, а в одной из них с единиц, то во второй а – с единиц;
если в одной совокупности а единиц, а во второй на с единиц меньше, то в ней а – с единиц;
если в одной совокупности а единиц, а во второй с (а > c) единиц, то в ней на а – с единиц меньше.
5. При умножении однозначного числа на однозначное пользуются таблицей умножения. Для умножения больших чисел пользуются правилами умножения «в столбик», основанными на распределительном свойстве умножения.
Например, 4378× 345 = 4378(300 + 40 + 5) = 4378× 300 + 4378× 40 + 4378× 5 =
= 1313400 + 175120 + 21890 = 1510410.
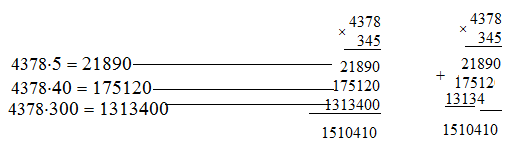
6. Чтобы найти остаток от деления одного натурального числа на другое, можно:
1) подобрать наибольшее число, которое при умножении на делитель даёт число, не превосходящее делимого;
2) из делимого вычесть произведение делителя на это число.
Например, чтобы найти остаток от деления числа 83 на 7:
1) подбираем наибольшее число, которое при умножении на 7 даёт число, не большее делимого 83: 7× 10 = 70, 7× 11 = 77, 7× 12 = 84. Число 77 меньше числа 83, а 84 больше этого числа. Искомое число — 11;
2) из делимого вычитаем произведение делителя на это число: 83 – 77 = 6.
Полученная разность 6 и есть искомым остатком.
7. Примените распределительный закон умножения относительно сложения или вычитания:
a× c + b× c = (a + b)× c; a× c – b× c = (a – b)× c.
Например, 73× 49 + 27× 49 = (73 + 27)× 49 = 100× 49 = 4 900.
8. Воспользуйтесь соотношениями:
Например, чтобы найти, какую часть минуты составляет 7 с, воспользуемся тем, что 1 с = 
мин. Поэтому 7 с = 
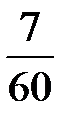мин.
9. Если значение некоторой величины разделено на известное количество равных частей, то чтобы найти значение одной части, нужно значение величины разделить на количество частей.
|
|
|
Например, если на швейной фабрике из 30 м ткани сшили 12 одинаковых платьев, то на 1 платье потребовалось 30: 12 = 2, 5 (м) ткани.
10. Чтобы найти дробь от числа, нужно:
|
|
|
