 |
13.Воспользуйтесь основным свойством дроби.
|
|
|
|
13. Воспользуйтесь основным свойством дроби.
Если числитель и знаменатель дроби умножить на одно и то же число или разделить на число, не равное нулю, то получится дробь, равная данной: .
С помощью основного свойства можно также упрощать дроби, заменяя дробь равной, но с меньшими числителем и знаменателем, то есть сокращать дроби.
Для выполнения задания нужно данный знаменатель дроби или искомый разложить на множители.
14. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить прежним.
Чтобы найти разность дробей с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй, а знаменатель оставить прежним.
Если нужно найти сумму или разность дробей с разными знаменателями, то их предварительно приводят к общему знаменателю.
Например, 
. Вначале нашли наименьший общий знаменатель (НОЗ)данных дробей, то есть наименьшее общее кратное чисел 30 и 12.
Наименьшее общее кратное двух чисел равно произведению одного из этих множитель на простые множители второго числа, не входящие в разложение первого.
30 = 2× 3× 5, 12 = 2× 2× 3. Тогда НОЗ (30, 12) = 30× 2 = 60.
Затем находим для каждой дроби дополнительные множители и умножаем на них числители дробей: 60: 30 = 2, 60: 12 = 5, 11× 2 = 22, 7× 5 = 35. Полученную дробь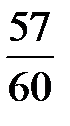 
можно сократить на 3: 
.
При приведении дробей к наименьшему общему знаменателю полезно различать такие частные случаи:
- один из знаменателей кратен другому, тогда этот знаменатель и будет наименьшим общим знаменателем данных дробей;
- знаменатели — взаимно обратные числа, тогда наименьшй общий знаменатель равен произведению знаменателей данных дробей.
|
|
|
Если требуется выполнить вычисления со смешанными числами, то обычно компоненты действий представляют в виде неправильных дробей и выполняют действия, как с обычными дробями.
15. Воспользуйтесь правилом умножения дроби на дробь.
Чтобы умножить дробь на дробь, нужно перемножить их числители и их знаменатели и первое произведение записать числителем, а второе — знаменателем: .
При умножении дроби на натуральное число нужно записать натуральное число в виде дроби со знаменателем 1.
При умножении дроби на смешанное число или при умножении смешанных чисел нужно смешанное число представить в виде неправильной дроби.
Например,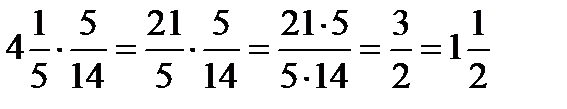 
.
16. Чтобы разделить одну дробь на другую, нужно первую дробь умножить на дробь, обратную данной, то есть такую, которая получается из делителя переменой местами числителя и знаменателя.
Если делимое или делитель является натуральным числом или смешанной дробью, то перед выполнением деления его надо представить в виде неправильной дроби.
Например, 
.
17. Для решения задачи нужно найти число по значению его дроби.
Чтобы найти число по его дроби, нужно данное значение дроби числа разделить на числитель дроби и умножить на знаменатель.
Например, если 120 км составляет 
некоторого расстояния, то разделив 120 (значение дроби от всего расстояния) на 3 (числитель дроби), найдём 
всего расстояния, умножив частное 40 на 4 (знаменатель дроби), найдём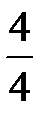 
или всё расстояние.
18. В задании требуется разместить некоторое количество продукции (или людей) в определённых ёмкостях или автобусах одинаковой вместимости. Обратите внимание на то, что полном заполнении какого-то количества ёмкостей (автобусов) ещё остаётся некоторое количество продукции (людей).
Фактически требуется найти увеличенное на 1 неполное частное от деления одного числа на другое.
|
|
|
Чтобы найти неполное частное от деления одного натурального числа на другое, нужно выполнить деление «уголком» до получения остатка, меньшего делителя.
Например, чтобы найти частное и остаток от деления числа 85 на 6:
1) выполняем деление «уголком»;
2) получили неполное частное 14 и остаток 1.
Не забудьте перевести все значения в одни и те же единицы измерения.
Если требуется разместить 4 л молока в бутылках ёмкостью 
л каждая, то разделив 4 л на 
л, мы получим в частном 2 (т. е. 2 полные бутылки) и еще некоторый остаток. Но для этого остатка нужна еще одна бутылка (пусть и неполная).
19. В задании требуется фактически найти два значения по их сумме или разности и их отношению. Это так называемая задача на части. Примите меньшее значение за 1 часть, найдите, сколько частей составляет второе значение и их сумма или разность. Затем найдите значение, принятое за 1 часть.
Можно составить и решить уравнение.
19. В задании требуется по сумме трёх слагаемых и двум известным слагаемым найти третье. Для этого от известной суммы нужно вычесть сумму двух известных слагаемых.
Если в качестве слагаемых предлагаются доли целого, то целое принимается за 1.
|
|
|
