 |
1) данное число разделить на знаменатель дроби, то есть найти, сколько приходится на одну часть;
|
|
|
|
1) данное число разделить на знаменатель дроби, то есть найти, сколько приходится на одну часть;
2) полученный результат умножить на числитель, который показывает, сколько равных частей данного числа взято.
Например, если в классе из 30 человек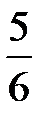 
занимается спортом, то для нахождения количества учащихся, занимающихся спортом, нужно:
1) разделить число 30 на знаменатель дроби 6: 30: 6 = 5;
2) полученный результат 5 умножить на числитель дроби 5: 5× 5 = 25.
11. В задачах, в которых речь идёт о стоимости, как правило, фигурируют три величины:
— 
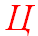цена продукции, то есть стоимость одной единицы этой продукции (это может быть один экземпляр, или 1 килограмм, или 1 литр, или какая-то иная единица);
— 
количество единиц продукции (оно может измеряться в штуках, килограммах, литрах и т. д. );
— стоимость всей продукции, равная произведению цены на количество всей продукции:
С = К× Ц.
По заданным значениям двух из трёх перечисленных величин можно найти третью.
Цена равна частному от деления стоимости на количество продукции: 
.
Количество продукции равно частному от деления стоимости на цену: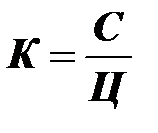 
.
12. Воспользуйтесь тем, что
При прямолинейном равномерном движении в противоположных направлениях скорость сближения (или удаления) равна сумме скоростей.
13. Обратите внимание на то, что фактически нужно найти наибольший общий делитель числителя и знаменателя.
Наибольший общий делитель двух чисел равен произведению общих простых множителей, на которые разлагаются эти числа.
Например, если требуется найти наибольшее число, на которое можно разделить числитель и знаменатель дроби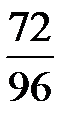 
, то вначале разлагаем 72 и 96 на простые множители: 72 = 2× 2× 2× 3× 3, 96 = 2× 2× 2× 2× 2× 3. Затем находим произведение общих простых множителей 2× 2× 2× 3 = 24. Это и есть искомое число.
|
|
|
14. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить прежним.
Если нужно найти сумму дробей с разными знаменателями, то их предварительно приводят к общему знаменателю.
Например, 
. Вначале нашли наименьший общий знаменатель (НОЗ)данных дробей, то есть наименьшее общее кратное чисел 30 и 12.
Наименьшее общее кратное двух чисел равно произведению одного из этих множитель на простые множители второго числа, не входящие в разложение первого.
30 = 2× 3× 5, 12 = 2× 2× 3. Тогда НОЗ (30, 12) = 30× 2 = 60.
Затем находим для каждой дроби дополнительные множители и умножаем на них числители дробей: 60: 30 = 2, 60: 12 = 5, 11× 2 = 22, 7× 5 = 35. Полученную дробь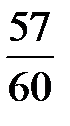 
можно сократить на 3: 
.
15. Воспользуйтесь правилом умножения дроби на натуральное число.
Чтобы умножить дробь на натуральное число, нужно умножить на это число её числитель, не меняя знаменатель.
16. Воспользуйтесь правилом деления дроби на натуральное число.
Чтобы разделить дробь на натуральное число, нужно умножить её знаменатель на это число, не меняя числитель.
17. В задаче требуется найти дробь от числа.
Чтобы найти дробь от числа, надо это число умножить на данную дробь.
Чтобы умножить дробь на натуральное число, нужно умножить на это число числитель дроби.
Чтобы найти произведение двух дробей, нужно произведение их числителей записать в числитель результата, а произведение их знаменателей записать в знаменатель результата.
Например, если площадь поля составляет 3 га, а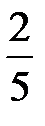 
этого поля засеяли рожью, то для нахождения площади, засеянной рожью, нужно найти 
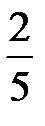от 3 га. Для этого нужно умножить 3 на 
. Получим: 3× = 
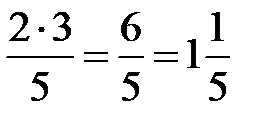га.
|
|
|
|
|
|
