Преобразование координат точек фотограмметрической модели в систему координат местности

Рис. 10.1. Варианты технологии построения фотограмметрической модели

Построение фотограмметрической модели в произвольно выбранной системе координат представляется чуть более сложным, но в ряде случаев это вполне оправдано конкретными условиями обработки данных.

Построение фотограмметрической модели по трем аэроснимкам

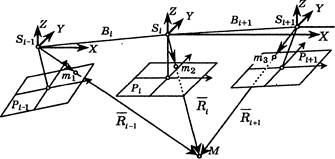
Три смежных снимка, принадлежащие двум смежным стереопарам и имеющие зону тройного продольного перекрытия, образуют фо­тограмметрический триплет. Средний снимок S\ {рис. Ю.2) и точки тройного продольного перекрытия входят как в предыдущую стереопару (*-1, i), так и в последующую (i, i+1).

Фотограмметрический триплет строится в координатной системе S_tXYZ, начало которой совмещено с центром фотографирования

*-х

 

Рис. 10.2. Фотограмметрический триплет

среднего снимка S_t (рис. 10.2), а оси X и Y параллельны осям коорди­нат его внутренней координатной системы оху. Взаимное ориентиро­вание снимков триплета выполняется в линейно-угловой системе; до­полнительно к условиям компланарности соответствующих векторов в обеих стереопарах используется масштабное условие, требующее ра­венства длин проектирующих лучей для связующих точек, располо-женныхъ зоне тройного продольного перекрытия.

Названные условия выражаются тремя зависимостями, из которых две описывают условия компланарности для левой и правой стерео­пар, а третья - масштабное условие.

Оба условия компланарности должны быть записаны для коорди­натной системы, параллельной осям среднего снимка, но формы их записи для левой и правой стереопар будут различны. Так, в правой стереопаре PtPt+i координатная система аналогична принятой при выводе условия (9.18), а для левой стереопары Pt-\Pt условие компла­нарности в системе координат S_tXYZ записывается в виде:

вх	BY	вг
х\	у;	z[
\Х2	у-	-f

= 0

(10.1)

Условие совпадения длин проектирующих лучей Si-\M, SjM, и Si+iM (рис. 10.2) запишем, воспользовавшись равенствами (9.3):

N,

'т/х,² + Y; + Z] -N₂,JX$ + Y; + Z² = 0,

(10.2)

где N2 и Ni - скалярные множители, определяемые по формулам (9.2) в левой и правой стереопарах; Х_х, Yj, Z\ - координаты связую­щей точки, вычисленные в левой стереопаре относительно среднего

центра S_t\ X2, У2» Z2 - координаты тех же точек в правой стереопаре относительно того же центра S*.

С учетом изложенного уравнение поправок, возникающее при по­строении фотограмметрического триплета, имеет вид:

с?.5т. + <i,5v. + d,Act. + d,8Aco. + d.&Ay, + ]

. 1 2 1 3 1 4 1 5 *1 I _(ЮЗ)

+ <2₆8т₂ + d₇8v₂ + d₈Act₂ + d₉8Aw₂ + d₁₀8x₂ + d_N8b₂ + / = vj

где d\, d<i>... rfn - частные производные от функций (9.18), (10.1) и (10.2) по соответствующим неизвестным, а нижние индексы при эле­ментах взаимного ориентирования обозначают номер стереопары: ле­вая (1) или правая (2).

Решение уравнений (10.3) методом наименьших квадратов позво­ляет отыскать как элементы ориентирования крайних снимков относи­тельно среднего, так и поправку к базису фотографирования второй стереопары, что обеспечивает построение сдвоенной модели (трипле­та) в единой системе координат и в одном масштабе.

Обратим внимание на следующее.

Включение в фотограмметрическую сеть одной точки стереопары сопровождается выполнением минимум четырех измерений (коор­динаты, продольный и поперечный параллаксы), из которых три необ­ходимы для определения пространственных координат точки, а одно оставшееся измерение используется для определения элементов вза­имного ориентирования.

Для связующей точки, расположенной в зоне тройного продольно­го перекрытия, измеряются восемь величин (координаты и параллаксы в стереопарах 1-2 и 2-3), причем, ее координаты на среднем снимке измеряются дважды. Если в процессе предварительной обработки ко­ординаты этой точки на среднем снимке 2 усреднены, то останется шесть измерений, из которых три необходимы для определения про­странственных координат, два - для взаимного ориентирования сте­реопар, и остаётся лишь одно измерение, которое можно использовать для связи смежных моделей на основе условия равенства длин проек­тирующих лучей (10.2) или скалярных множителей N\ и N2-

Если же координаты связующей точки не усреднялись, то из вось­ми измерений три по-прежнему используются для нахождения про­странственных координат точки, два - для взаимного ориентирования, а три оставшихся можно использовать для объединения моделей на основе условия равенства трех координат связующих точек.

⇐ Предыдущая33343536373839404142Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: