 |
Трассировка и увеличение графиков
|
|
|
|
Трассировка позволяет очень точно изучить строение графика. Для того чтобы включить режим трассировки, щелкните в области графика правой кнопкой мыши и выберите в контекстном меню пункт Trace (Трассировка). В результате появится окно трассировки (рис. 16.26), а в поле графика Вы увидите две пересекающиеся пунктирные линии.

Рис. 16.26. Трассировка графика
Перемещая указатель мыши по графику, Вы тем самым передвигаете точку пересечения линий трассировки При этом координаты точки указываются с высокой точностью в окне трассировки в полях X-Value (Значение X) и Y-Value (Значение Y). Нажатие кнопки Сору X (Копировать X) или Copy Y (Копировать Y) копирует соответствующее число в буфер обмена. В дальнейшем его можно вставить в любое место документа или в маркер, нажав клавиши <Ctrl>+<V>.
Если установлен флажок Track Data Points (Следовать за рядом данных), как это показано на рис. 16.26, то линии трассировки следуют точно вдоль графика. Если нет, то они могут перемещаться по всей области графика.
Помимо трассировки, в Mathcad предусмотрена еще одна удобная возможность просмотра графика в увеличенном масштабе. Для вызова диалогового окна Zoom (Масштаб графика) выберите в контекстном меню, либо в меню Format (Формат) пункты Graph (График) и Zoom (Масштаб). После этого указателем мыши выберите прямоугольную область на графике, которую Вы планируете просмотреть в увеличенном масштабе (рис. 16.27), и нажмите кнопку Zoom (Увеличить). В результате часть графика будет прорисована более крупно (рис. 16.28). Далее можно либо продолжать изменять масштаб, либо вернуться к прежнему виду графика кнопкой Full View (Показать целиком), либо закрыть диалог Zoom для окончательной перерисовки графика в крупном масштабе (нажав кнопку ОК)
|
|
|
Возможно, Вам покажется более удобным вызов окон трассировки и масштабирования графиков с помощью панели инструментов Graph (График) (рис. 16.29). Эти кнопки доступны только при выделенном двумерном графике

Рис. 16.27. Управление масштабом графика
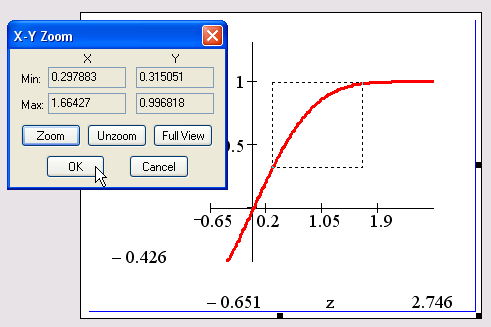
Рис. 16.28. Просмотр графика в увеличенном масштабе

Рис. 16.29. Кнопка трассировки на панели Graph, кнопка масштабирования — слева от нее
Трехмерные графики
Коллекция трехмерных графиков — настоящее чудо, которое Mathcad дарит пользователю. За считанные секунды Вы можете создать великолепную презентацию результатов своих расчетов.
16.4.1. Создание трехмерных графиков
Чтобы создать трехмерный график, требуется нажать кнопку с изображением любого из типов трехмерных графиков на панели инструментов Graph (График) (если возникнут сложности, обратитесь к. разд. 16.2). В результате появится пустая область графика с тремя осями (рис. 16.30) и единственным местозаполнителем в нижнем левом углу. В этот местозаполнитель следует ввести либо имя z функции z(x,y) двух переменных для быстрого построения трехмерного графика, либо имя матричной переменной z, которая задаст распределение данных zx,y на плоскости XY.
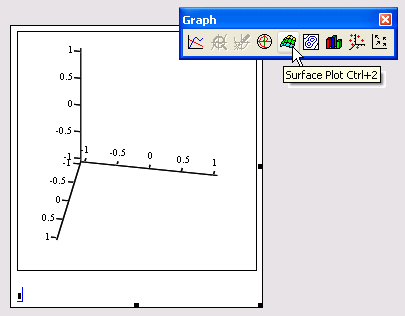
Рис. 16.30. Создание трехмерного графика
Рассмотрим на простом примере функции z(x,y) и матрицы z (они заданы в листингах 16.3 и 16.4, соответственно) примеры построения трехмерных графиков различных типов, создаваемых нажатием той или иной кнопки на панели Graph (График). Еще раз отметим, что для получения графиков не требуется никакого текста, кроме введения имени соответствующей функции или матрицы в местозаполнитель.
Для графиков, задаваемых матрицами, шкалу плоскости XY приходится задавать вручную. Mathcad просто рисует поверхность, точки в пространстве или линии уровня, основываясь на двумерной структуре этой матрицы. При быстром же построении графиков имеется возможность строить их в различном диапазоне аргументов, подобно двумерным графикам.
|
|
|
Листинг 16.3.Функция для быстрого построения трехмерных графиков

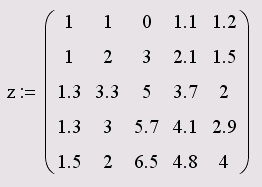
Листинг 16.4. Матрица для отображения на трехмерных графиках
Surface Plot - график поверхности (рис. 16.31 и 16.32)
Для построения графика поверхности необходимо воспользоваться клавишей Surface Plot панели инструментов Graph и следовать указаниям, описанным выше.

Рис. 16.31. Быстрое построение графика поверхности функции (листинг 16.3)
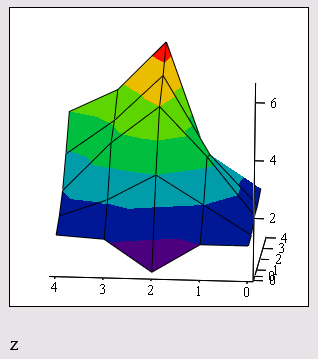
Рис. 16.32. График поверхности, заданный матрицей (листинг 16.4)
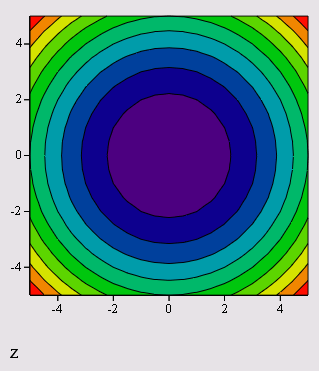
Рис. 16.33. Быстрое построение графика линий уровня функции (листинг 16.3)
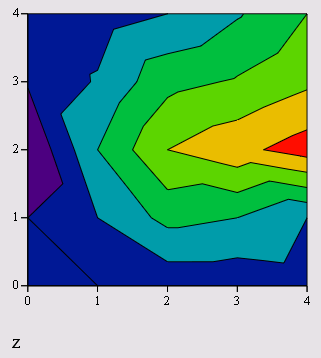
Рис. 16.34. График линий уровня, заданный матрицей (листинг 16.4)
Contour Plot - график линий уровня (рис. 16.33 и 16.34)
Для построения графика поверхности необходимо воспользоваться клавишей Contour Plot панели инструментов Graph и следовать указаниям, описанным выше.
3D Bar Plot - график трехмерной гистограммы (рис. 16.35 и 16.36)
Для построения графика поверхности необходимо воспользоваться клавишей 3D Bar Plot панели инструментов Graph и следовать указаниям, описанным выше.
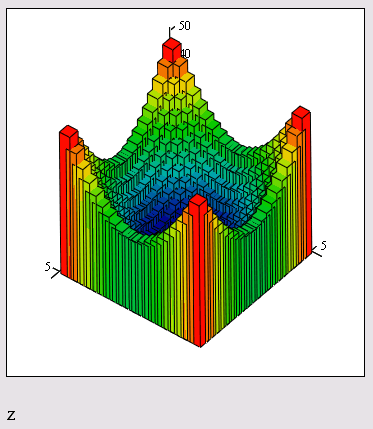
Рис. 16.35. Быстрое построение графика трехмерной гистограммы функции (листинг 16.3)

Рис. 16.36. График трехмерной гистограммы, заданный матрицей (листинг 16.4)

Рис. 16.37. Быстрое построение графика множества точек функции (листинг 16.3)

Рис. 16.38. График множества точек, заданный матрицей (листинг 16.4)
3D Scatter Plot - график множества точек (рис. 16.37 и 16.38)
Для построения графика поверхности необходимо воспользоваться клавишей 3D Scatter Plot панели инструментов Graph и следовать указаниям, описанным выше.
Vector Field Plot - график векторного поля (рис. 16.39)
График векторного поля несколько отличается от остальных типов двумерных графиков. Его смысл заключается в построении некоторого вектора в каждой точке плоскости XY. Чтобы задать вектор на плоскости, требуются два скалярных числа. Поэтому в Mathcad принято, что векторное поле задает комплексная матрица. Действительные части каждого ее элемента задают проекцию вектора на ось х, а мнимые — на ось у.
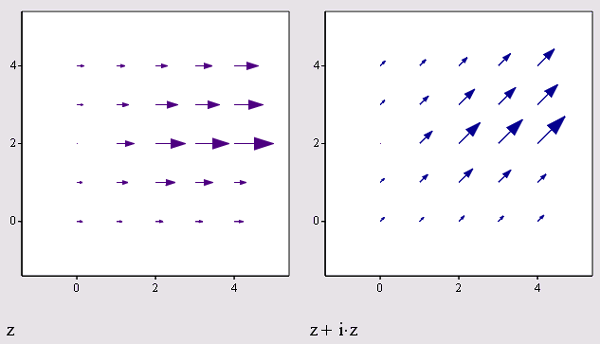
Рис. 16.39. Графики векторного поля, заданные матрицами (листинг 16.4)
|
|
|
Приведенные рисунки являются лишь первым шагом в создании красочных графиков. О том, как правильно отформатировать вновь созданные графики, чтобы они приобрели оптимальный с математической точки зрения и эффектный вид, рассказано в следующих разделах.
Улучшить трехмерное представление графика часто позволяет применение к исходным данным интерполяции (см. разд. "Многомерная интерполяция" гл. 15).
|
|
|


