 |
3.2 Электрическая проводимость растворов электролитов
|
|
|
|
Электролиты – вещества, диссоциирующие в растворах на ионы. Под влиянием приложенного электрического поля ионы движутся направленно и являются переносчиками зарядов. Следовательно, электролиты – ионные проводники, в отличие от электронных проводников – металлов. В зависимости от степени диссоциации 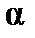 различают сильные и слабые электролиты. У сильных электролитов α ≈ 1. Степень диссоциации электролита в растворе зависит от природы вещества, концентрации и от природы растворителя.
различают сильные и слабые электролиты. У сильных электролитов α ≈ 1. Степень диссоциации электролита в растворе зависит от природы вещества, концентрации и от природы растворителя.
Электрической проводимостью wраствора называют величину, обратную сопротивлению R. Измеряется w в сименсах (1 См = 1 Ом-1). Электрическая проводимость раствора зависит от природы электролита и растворителя, концентрации, температуры и подвижностей ионов, образующихся при диссоциации электролита. Подвижность иона 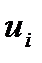 характеризует скорость его движения в поле с единичным градиентом потенциала. Различают удельную æ и молярную
характеризует скорость его движения в поле с единичным градиентом потенциала. Различают удельную æ и молярную 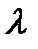 электрическую проводимости раствора.
электрическую проводимости раствора.
Удельная электрическая проводимость представляет собой электрическую проводимость единичного (1 м3) объема раствора, заключенного между параллельными электродами с единичной площадью (1 м2), расположенными на единичном расстоянии (1 м) друг от друга. Удельная электрическая проводимость является величиной, обратной удельному сопротивлению 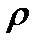 и измеряется в См× м-1:
и измеряется в См× м-1:
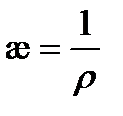 (3. 20)
(3. 20)
Удельное сопротивление определяется по уравнению:
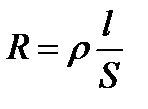 , (3. 21)
, (3. 21)
|
|
|
где R – общее сопротивление, Ом;
l – длина проводника, м;
S – поперечное сечение проводника, м2.
Если бы электричество проводили только ионы, находящиеся в растворе между электродами с единичной площадью, расположенными на единичном расстоянии, то измеряемая электрическая проводимость была бы удельной. В действительности ток проводят не только ионы, заключенные в этом единичном объеме. Поэтому удельная электрическая проводимость лишь пропорциональная общей проводимости w:
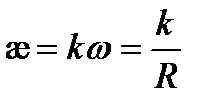 (3. 22)
(3. 22)
Коэффициент пропорциональности k называют константой сосуда, ее численное значение зависит от соотношения 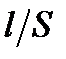 . Для нахождения константы сосуда измеряют сопротивление R стандартных растворов с известной удельной электрической проводимостью. В качестве стандартных растворов используют растворы KCl или NaCl, величины удельной электрической проводимости которых приводятся в справочной литературе. Например, [2], таблица 62, с. 119.
. Для нахождения константы сосуда измеряют сопротивление R стандартных растворов с известной удельной электрической проводимостью. В качестве стандартных растворов используют растворы KCl или NaCl, величины удельной электрической проводимости которых приводятся в справочной литературе. Например, [2], таблица 62, с. 119.
Пример : Вычислим удельную электрическую проводимость раствора KNO3, если сопротивление 0. 1 M раствора KCl при 25оС составляет 20 Ом, а сопротивление раствора KNO3, измеренное в тех же условиях, равно 254 Ом.
Решение :
Из табл. 62 [2] удельная электрическая проводимость раствора KCl æ = 1. 288 См× м-1. Следовательно, константа сосуда 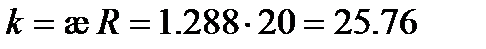 м-1 (или 0. 2576 см-1).
м-1 (или 0. 2576 см-1).
Удельная электрическая проводимость раствора KNO3, рассчитанная по (3. 22), равна
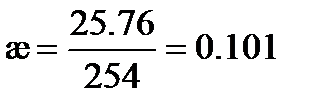 См× м-1.
См× м-1.
В растворах сильных электролитов удельная электрическая проводимость при увеличении концентрации раствора сначала возрастает, так как увеличивается количество ионов в единичном объеме. Но при некоторой концентрации æ достигает максимального значения, а затем начинает уменьшаться с ростом концентрации. Этот факт объясняется усилением электростатического взаимодействия между ионами, приводящим к уменьшению подвижности ионов.
|
|
|
В растворах слабых электролитов удельная электрическая проводимость слабо возрастает с увеличением концентрации раствора вследствие увеличения концентрации ионов. Подвижности ионов практически не изменяются с увеличением концентрации. Только в очень концентрированных вязких растворах подвижности ионов уменьшаются, что и приводит к снижению удельной электрической проводимости.
При изучении электрической проводимости растворов электролитов пользуются молярной электрической проводимостью 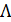 , которая равна удельной электрической проводимости, отнесенной к единичной концентрации раствора c:
, которая равна удельной электрической проводимости, отнесенной к единичной концентрации раствора c:
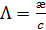 , (3. 23)
, (3. 23)
где c - концентрация, выраженная в моль/м3.
Размерность 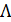 См× м2/моль.
См× м2/моль.
Если концентрация выражена в моль/л, то уравнение (3. 23) будет иметь вид
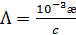 (3. 23а)
(3. 23а)
Для практических расчетов часто используются размерности в производных единицах СИ: [æ ] - Cм× см-1; [ 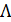 ] - См× см2/моль, [c] - моль/л. При этом вместо уравнения (3. 23) используют соотношение
] - См× см2/моль, [c] - моль/л. При этом вместо уравнения (3. 23) используют соотношение
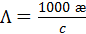 (3. 23б)
(3. 23б)
Пример: Вычислим удельную и молярную электрические проводимости 0. 1 М раствора KNO3, если удельное сопротивление раствора составляет 95. 3 Ом× см.
Решение :
Удельная электрическая проводимость раствора в соответствие с (3. 20) будет равна
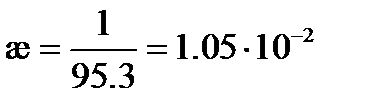 См× см-1
См× см-1
Молярная электрическая проводимость, вычисленная по (3. 23б), составит
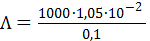 = 105 См× см2/моль
= 105 См× см2/моль
С увеличением концентрации электролита молярная электрическая проводимость уменьшается. Для сильных электролитов это связано с уменьшением подвижности ионов вследствие усиления межионного взаимодействия, а для слабых – в основном с уменьшением степени диссоциации. Молярная электрическая проводимость с уменьшением концентрации увеличивается и при с → 0 стремится к некоторому предельному максимальному значению 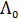 . Величину предельного значения молярной электрической проводимости можно рассчитать, используя закон Кольрауша о независимом движении ионов:
. Величину предельного значения молярной электрической проводимости можно рассчитать, используя закон Кольрауша о независимом движении ионов:
|
|
|
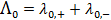 , (3. 24)
, (3. 24)
где 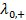 и
и 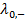 – предельные электрические проводимости ионов, образующих электролит.
– предельные электрические проводимости ионов, образующих электролит.
Величины предельных электрических проводимостей отдельных ионов приведены в справочниках, например в [2], таблица 65, с. 123.
Для сильных электролитов имеется линейная зависимость 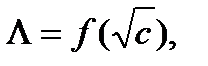 поэтому величину
поэтому величину 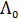 можно найти экстраполяцией этой линейной зависимости к с → 0.
можно найти экстраполяцией этой линейной зависимости к с → 0.
Так как уменьшение молярной электрической проводимости слабого электролита объясняется, в основном, снижением степени диссоциации, то величину степени диссоциации при заданной концентрации раствора можно определить из соотношения:
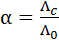 , (3. 25)
, (3. 25)
где 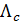 - величина молярной электрической проводимости при заданной концентрации раствора c.
- величина молярной электрической проводимости при заданной концентрации раствора c.
Определив степень диссоциации слабого электролита, легко рассчитать практическую константу диссоциации при данной концентрации
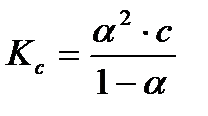 (3. 26)
(3. 26)
В справочной литературе приводятся величины молярной электрической проводимости ряда слабых электролитов при различных разведениях раствора V, например, [2], таблица 66, с. 125.
Пример: Используя справочное значение молярной электрической проводимости трихлоруксуной кислоты при разведении раствора V = 256 л/моль, вычислим степень, константу диссоциации и рН данного раствора при температуре 25оС.
Решение:
Из таблицы 66 [2] следует, что при разведении V = 256 л/моль величина 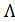 = 371. 4× 10-4 См× м2/моль. Трихлоруксусная кислота диссоциирует по уравнению
= 371. 4× 10-4 См× м2/моль. Трихлоруксусная кислота диссоциирует по уравнению
|
|
|
CCl3COOH Û H+ + CCl3COO-
В таблице 65 при 25оС находим значения 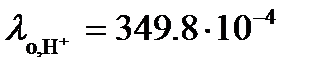 См× м2/моль и
См× м2/моль и  См× м2/моль.
См× м2/моль.
Тогда в соответствие с (3. 24)
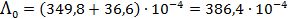 См× м2/моль.
См× м2/моль.
Степень диссоциации вычисляем по уравнению (3. 25)
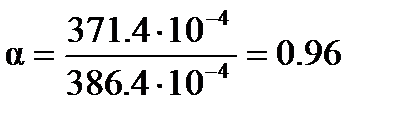 .
.
Концентрация раствора кислоты при данном разведении составляет
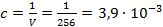 ,
,
следовательно, константа диссоциации, рассчитанная по уравнению (3. 26), равна
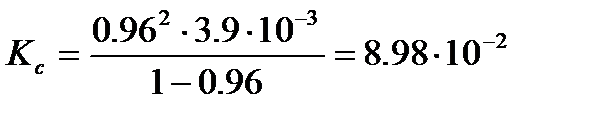
рН раствора определяется активностью ионов водорода. Так как раствор достаточно разбавленный, можно считать его близким к идеальному и вместо активности использовать концентрацию ионов водорода:
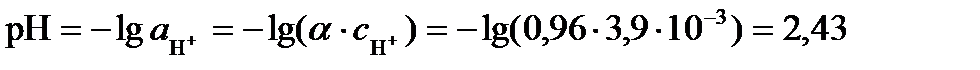
Измерения электрической проводимости используют для нахождения растворимости или произведения растворимости трудно растворимых соединений. Такие насыщенные растворы можно считать близкими к бесконечно разбавленным и поэтому принять 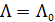 .
.
Пример : Насыщенный раствор AgCl имеет при 25оС в сосуде с константой k = 0. 18 см-1 сопротивление R = 67542 Ом, 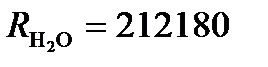 Ом. Вычислим произведение растворимости AgCl, считая, что растворенная соль полностью диссоциирована.
Ом. Вычислим произведение растворимости AgCl, считая, что растворенная соль полностью диссоциирована.
Решение: .
Так как растворимость мала, то можно считать, что 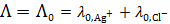 . Из таблицы 65 [2] следует, что
. Из таблицы 65 [2] следует, что 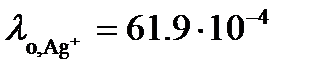 См× м2/моль, а
См× м2/моль, а 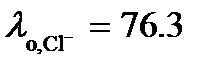 См× м2/моль.
См× м2/моль.
Тогда
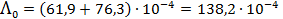 См× м2/моль = 138. 2 См× см2/моль.
См× м2/моль = 138. 2 См× см2/моль.
Для раствора AgCl
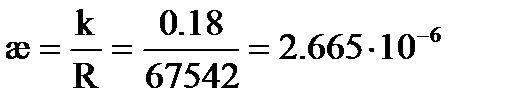 См× см-1,
См× см-1,
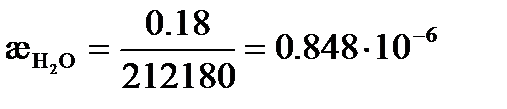 См× см-1,
См× см-1,
следовательно,
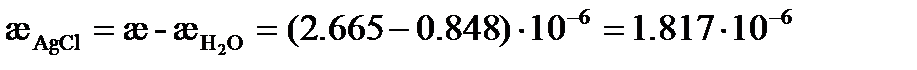 См× см-1.
См× см-1.
Растворимость
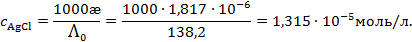
Так как растворимость мала, можно считать раствор близким к идеальному, и тогда произведение растворимости
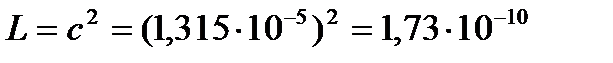 (моль/л)2.
(моль/л)2.
|
|
|


