Главная | Обратная связь | Поможем написать вашу работу!

4.2.4 Многовариантное задание № 11 «Вращательные спектры двухатомных молекул»

Решение

В приближении модели жесткого ротатора в соответствии с уравнением (4. 45) определяем вращательную постоянную:

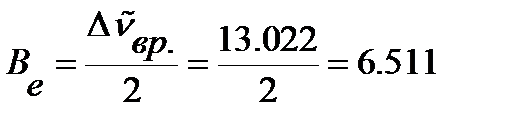см^-1.

Момент инерции молекулы вычисляем из значения вращательной постоянной по уравнению (4. 46):

кг ^.м².

Для определения равновесного межъядерного расстояния используем уравнение (4. 47), учитывая, что массы ядер водорода и йода 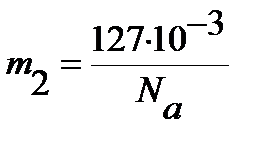выражены в кг:

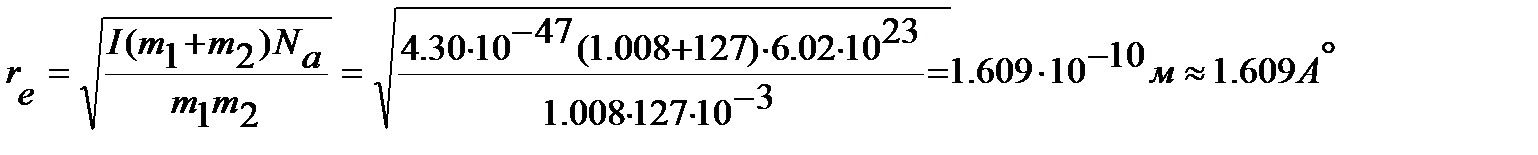
Пример. В дальней ИК-области спектра ¹H³⁵Cl обнаружены линии, волновые числа которых:

N линии
, см^-1	85. 384	106. 730	128. 076	149. 422	170. 768	192. 114	213. 466

Определите усредненные значения момента инерции и межъядерного расстояния молекулы. Отнесите наблюдаемые линии в спектре к вращательным переходам.

Решение

Согласно модели жесткого ротатора разность волновых чисел соседних линий вращательного спектра постоянна и равна 2 . Определим вращательную постоянную по среднему значению расстояний между соседними линиями в спектре:

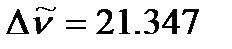см^-1,

см^-1

Находим момент инерции молекулы (уравнение (4. 46)):

кг·м²

Рассчитываем равновесное межъядерное расстояние (уравнение (4. 47)), принимая во внимание, что массы ядер водорода и хлора (выражены в кг):

По уравнению (4. 43) оцениваем положение линий во вращательном спектре ¹H³⁵Cl:

…

и т. д.

Соотносим рассчитанные значения волновых чисел линий с экспериментальными. Получается, что наблюдаемые во вращательном спектре ¹H³⁵Cl линии соответствуют переходам:

N линии
, см^-1	85. 384	106. 730	128. 076	149. 422	170. 768	192. 114	213. 466
	3 4	4 5	5 6	6 7	7 8	8 9	9 10

Пример. Определите величину и направление изотопного сдвига линии поглощения, отвечающей переходу с энергетический уровень, во вращательном спектре молекулы ¹H³⁵Cl при замещении атома хлора на изотоп ³⁷Cl. Межъядерное расстояние в молекулах ¹H³⁵Cl и ¹H³⁷Cl считать одинаковым.

Решение

Для определения величины изотопного сдвига линии, отвечающей переходу , рассчитываем приведенную массу молекулы ¹H³⁷Cl с учетом изменения атомной массы ³⁷Cl:

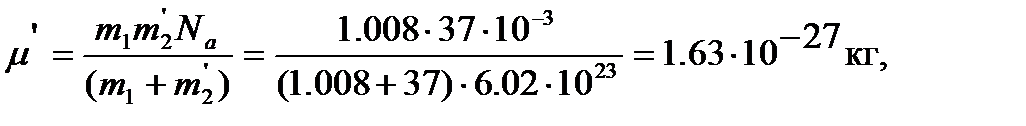
далее вычисляем момент инерции , вращательную постоянную и положение линии в спектре молекулы ¹H³⁷Cl и величину изотопного сдвига по уравнениям (4. 35), (4. 39), (4. 43) и (4. 50), соответственно.

Иначе изотопный сдвиг можно оценить из отношения волновых чисел линий, отвечающих одному и тому же переходу в молекулах, (межъядерное расстояние считаем постоянным) и далее положение линии в спектре, используя уравнение (4. 51).

Для молекул ¹H³⁵Cl и ¹H³⁷Cl отношение волновых чисел заданного перехода равно:

Для определения волнового числа линии изотопозамещенной молекулы подставляем найденное в предыдущем примере значение волнового числа перехода j → j+1 (3→ 4):

Делаем вывод: изотопный сдвиг в низкочастотную или длинноволновую область составляет

85. 384 - 83. 049 = 2. 335 см^-1.

Пример. Рассчитайте волновое число и длину волны наиболее интенсивной спектральной линии вращательного спектра молекулы ¹H³⁵Cl. Соотнесите линию с соответствующим вращательным переходом.

Решение

Наиболее интенсивная линия во вращательном спектре молекулы связана с максимальной относительной заселенностью вращательного уровня энергии.

Подстановка найденного в предыдущем примере значения вращательной постоянной для ¹H³⁵Cl ( см^-1) в уравнение (4. 54) позволяет вычислить номер этого уровня энергии:

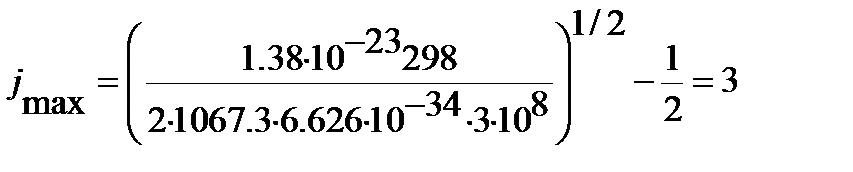Волновое число вращательного перехода с этого уровня рассчитываем по уравнению (4. 43):

Длину волны перехода находим из преобразованного относительно уравнения (4. 11):

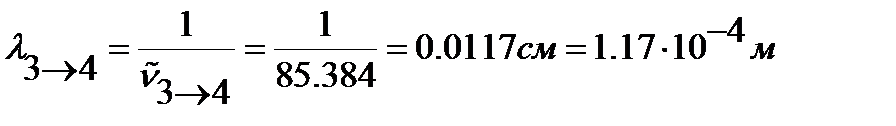4. 2. 4 Многовариантное задание № 11 «Вращательные спектры двухатомных молекул»

1. Напишите квантово-механическое уравнение для расчета энергии вращательного движения двухатомной молекулы как жесткого ротатора.

2. Выведите уравнение для расчета изменения энергии вращения двухатомной молекулы как жесткого ротатора при переходе ее на соседний, более высокий квантовый уровень .

3. Выведите уравнение зависимости волнового числа вращательных линий в спектре поглощения двухатомной молекулы от вращательного квантового числа.

4. Выведите уравнение для расчета разности волновых чисел соседних линий во вращательном спектре поглощения двухатомной молекулы.

5. Рассчитайте вращательную постоянную (в см^-1и м^-1) двухатомной молекулы A по волновым числам двух соседних линий в длинноволновой инфракрасной области вращательного спектра поглощения молекулы (см. таблицу 4. 3).

6. Определите энергию вращения молекулы A на первых пяти квантовых вращательных уровнях (Дж).

7. Вычертите схематически энергетические уровни вращательного движения двухатомной молекулы как жесткого ротатора.

8. Нанесите пунктиром на эту схему вращательные квантовые уровни молекулы, не являющейся жестким ротатором.

9. Выведите уравнение для вычисления равновесного межъядерного расстояния на основании разности волновых чисел соседних линий во вращательном спектре поглощения.

10. Определите момент инерции (кг^.м²) двухатомной молекулы A.

11. Рассчитайте приведенную массу (кг) молекулы A.

12. Вычислите равновесное межъядерное расстояние 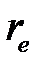( ) молекулы A. Сопоставьте полученное значение со справочными данными.

13. Отнесите наблюдаемые линии во вращательном спектре молекулы A к вращательным переходам.

14. Рассчитайте волновое число спектральной линии, отвечающей вращательному переходу с уровня j для молекулы A (см. таблицу 4. 3).

15. Вычислите приведенную массу 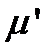(кг) изотопозамещенной молекулы B.

16. Рассчитайте волновое число спектральной линии, связанной с вращательным переходом с уровня j для молекулы B (см. таблицу 4. 3). Межъядерные расстояния в молекулах A и B считать равными.

17. Определите величину и направление изотопного сдвига во вращательных спектрах молекул A и B для спектральной линии, отвечающей переходу с вращательного уровня j.

18. Объясните причину немонотонного изменения интенсивности линий поглощения по мере увеличения энергии вращения молекулы

19. Определите квантовое число вращательного уровня, отвечающего наибольшей относительной заселенности. Рассчитайте длины волн наиболее интенсивных спектральных линий вращательных спектров молекул A и B.

Таблица 4. 3 – Варианты заданий

Вариант	Молекула A	Под вариант			j	Молекула B
	LiH		60. 12	75. 15		Li²H
			180. 36	195. 39		⁸LiH
			195. 39	210. 42		⁶Li³H
			105. 21	120. 24		Li³H
			120. 24	135. 27		⁶LiH
			90. 18	105. 21		⁶Li²H
	BCl		4. 104	5. 472		B³⁷Cl
			8. 208	9. 576		¹⁰BCl
			9. 576	10. 944		B³⁷Cl
			10. 944	12. 312		¹⁰B³⁷Cl
			12. 312	13. 68		¹⁰BCl
			17. 784	19. 152		B³⁷Cl
	BeH		103. 15	123. 78		Be²H
			82. 52	103. 15		Be³H
			226. 93	247. 56		⁵BeH
			247. 56	268. 19		¹¹BeH
			185. 67	206. 3		¹³BeH
			206. 3	226. 93		¹⁶BeH
	CO		11. 534	15. 379		¹³CO
			23. 068	26. 913		C¹⁷O
			26. 913	30. 757		¹⁷CO
			30. 757	34. 602		C¹⁸O
			34. 602	38. 447		¹⁴CO
			53. 825	57. 670		¹⁵CO
	HBr		33. 88	50. 82		³HBr
			152. 48	169. 42		²HBr
			203. 30	220. 25		H⁷⁷Br
			186. 36	203. 30		H⁸⁵Br
			169. 42	186. 36		H⁸⁴Br
			220. 25	237. 19		H⁸²Br
	HCl		169. 44	190. 62		²HCl
			232. 98	254. 16		³HCl
			127. 08	148. 26		H³⁷Cl
			105. 90	127. 08		³HCl
			254. 16	275. 34		²H³⁷Cl
			148. 26	169. 44		³H³⁷Cl
	LiF		5. 38	8. 07		⁶LiF
			24. 21	26. 90		⁶Li¹⁸F
			16. 14	18. 83		Li¹⁸F
			13. 45	16. 14		⁶LiF
			21. 52	24. 21		⁶Li¹⁸F
			18. 83	21. 52		⁶LiF

Продолжение таблицы 4. 3

Вариант	Молекула A	Под вариант			j	Молекула B
	HI		39. 066	52. 088		²HI
			91. 154	104. 176		³HI
			143. 242	156. 264		²H¹²⁹I
			104. 176	117. 198		³H¹³¹I
			130. 220	143. 242		H¹²⁹I
			117. 198	130. 220		H¹³¹I
	CsI		0. 0944	0. 1416		Cs¹²⁵I
			0. 5192	0. 5664		¹³⁵Cs¹²⁵I
			0. 6608	0. 7080		¹³⁴Cs¹²⁹I
			0. 6136	0. 6608		Cs¹²⁹I
			0. 5664	0. 6136		¹³⁵CsI
			0. 7080	0. 7552		¹³⁴CsI
	OH		189. 20	227. 04		O²H
			416. 24	454. 08		¹⁷O²H
			491. 92	529. 76		¹⁷OH
			567. 60	605. 44		O³H
			529. 76	567. 60		¹⁸O²H
			454. 08	491. 92		¹⁸OH
	NaH		29. 40	39. 20		Na²H
			58. 80	68. 60		²⁴Na²H
			127. 40	137. 20		²²NaH
			98. 00	107. 80		²⁴NaH
			88. 20	98. 00		²²Na³H
			137. 20	147. 00		Na³H
	SiH		45. 01	59. 99		Si²H
			165. 00	180. 00		Si³H
			105. 00	120. 00		²⁹SiH
			195. 00	210. 00		²⁹Si²H
			225. 00	240. 00		³⁰SiH
			210. 00	225. 00		³⁰Si³H
	HF		123. 15	164. 00		²HF
			205. 25	246. 30		³H¹⁸F
			246. 30	287. 35		²H¹⁸F
			492. 60	533. 65		³HF
			533. 65	574. 70		H¹⁸F
			369. 45	410. 50		²HF
	NO		17. 05	20. 46		N¹⁸O
			44. 33	47. 74		N¹⁷O
			34. 10	37. 51		¹⁵N¹⁸O
			30. 69	34. 10		¹⁵NO
			40. 92	44. 33		¹⁵N¹⁷O
			37. 51	40. 92		¹³NO

Продолжение таблицы 4. 3

Вариант	Молекула A	Под вариант			j	Молекула B
	SO		8. 64	10. 08		S¹⁸O
			18. 72	20. 16		³⁴SO
			14. 40	15. 84		S¹⁷O
			17. 28	18. 72		³⁶SO
			15. 84	17. 28		³³S¹⁷O
			12. 96	14. 40		³³SO
	ClO		6. 25	7. 50		³⁷ClO
			13. 75	15. 00		Cl¹⁷O
			18. 75	20. 00		³⁷Cl¹⁸O
			12. 50	13. 75		Cl¹⁸O
			15. 00	16. 25		³⁷Cl¹⁷O
			10. 00	11. 25		³⁷ClO
	CN		3. 80	7. 60		¹³C N
			15. 20	19. 00		¹³C¹⁵N
			38. 00	41. 80		¹⁴CN
			22. 80	26. 60		C¹³N
			53. 20	57. 00		C¹⁵N
			30. 40	34. 20		¹³C¹³N
	SH		95. 95	115. 14		S²H
			211. 09	230. 28		³³S²H
			268. 66	287. 85		³³S³H
			191. 90	211. 09		³⁴S²H
			172. 71	191. 90		³⁴S³H
			153. 52	172. 71		S³H
	FO		8. 84	11. 05		F¹⁸O
			22. 10	24. 31		F¹⁷O
			15. 47	17. 68		F¹⁸O
			19. 89	22. 10		¹⁸FO
			17. 68	19. 89		¹⁸F¹⁸O
			13. 26	15. 47		¹⁸F¹⁷O
	HB		144. 24	168. 28		²HB
			216. 36	240. 4		³HB
			240. 4	264. 44		²H¹⁰B
			264. 44	288. 48		³H¹⁰B
			96. 16	120. 2		H¹⁰B
			120. 2	144. 24		³HB
	PH		51. 74	69. 04		P²H
			138. 08	155. 34		P³H
			224. 38	241. 64		P²H
			103. 56	120. 82		³⁰P³H
			120. 82	138. 08		³⁰P²H
			172. 6	189. 86		P²H

Продолжение таблицы 4. 3

Вариант	Молекула A	Под вариант			j	Молекула B
	BeO		13. 20	16. 50		Be¹⁸O
			52. 8	56. 10		Be¹⁷O
			39. 6	42. 90		Be¹⁸O
			26. 4	29. 70		⁷BeO
			46. 2	49. 50		⁷Be¹⁸O
			19. 8	23. 10		⁷Be¹⁷O
	NH		133. 32	166. 65		N²H
			433. 29	466. 62		N³H
			333. 3	366. 63		¹⁵NH
			399. 96	433. 29		¹³NH
			299. 97	333. 30		¹⁵N²H
			366. 63	399. 96		¹⁵N³H
	²H⁸¹Br		16. 9795	25. 4640		²H⁷⁹Br
			59. 416	67. 90		³H⁷⁹Br
			110. 344	118. 83		²H⁸⁰Br
			76. 392	84. 88		³H⁸⁰Br
			127. 32	135. 81		H⁷⁹Br
			93. 368	101. 86		H⁸⁰Br
	NaO		5. 95	6. 80		Na¹⁸О
			7. 65	8. 50		²⁴Na¹⁸О
			12. 75	13. 60		²²NaО
			9. 35	10. 20		²⁴NaО
			4. 25	5. 10		²²Na¹⁸О
			11. 05	11. 90		Na¹⁷О
	LiO		9. 64	12. 05		Li¹⁸O
			16. 87	19. 28		⁸LiO
			31. 33	33. 74		⁶LiO
			21. 69	24. 10		Li¹⁸O
			36. 15	38. 56		⁶LiO
			26. 51	28. 92		⁶Li¹⁸O
	H³⁷Cl		42. 56	63. 83		H³⁵Cl
			106. 35	127. 62		²H³⁵Cl
			276. 51	297. 78		³H³⁵Cl
			148. 89	170. 16		²H³⁷Cl
			233. 97	255. 24		³H³⁷Cl
			191. 43	212. 70		²H³⁵Cl
	CH		144. 55	173. 46		C²H
			404. 74	433. 65		¹³C²H
			289. 1	318. 01		C³H
			462. 56	491. 47		¹³C³H
			346. 92	375. 83		¹³C²H
			173. 46	202. 37		C²H

Продолжение таблицы 4. 3

Вариант	Молекула A	Под вариант			j	Молекула B
	SiO		7. 25	8. 70		Si¹⁸O
			10. 15	11. 60		Si¹⁷O
			18. 85	20. 30		²⁹Si¹⁸O
			13. 05	14. 50		³⁰Si¹⁷O
			21. 75	23. 20		²⁹SiO
			15. 95	17. 40		³⁰SiO

⇐ Предыдущая 22 23 24 25 262728 29 30 31 Следующая ⇒

Воспользуйтесь поиском по сайту: