 |
3.2.1 Многовариантное задание № 9 «Электрическая проводимость растворов электролитов»
|
|
|
|
3. 2. 1 Многовариантное задание № 9 «Электрическая проводимость растворов электролитов»
Используя величину удельного сопротивления r раствора при температуре 25º С электролита А заданной концентрации c (таблица 3. 5), рассчитать степень, константу диссоциации и рН раствора.
3. 3 Контрольные вопросы
1. Что такое гальванический элемент?
2. Из чего состоит электрод электрохимической системы?
3. Каковы причины возникновения скачка потенциала на границе раздела проводник первого рода проводник второго рода?
4. Что такое водородная шкала потенциалов?
5. Как рассчитывается потенциал электрода в водородной шкале?
6. Каков физический смысл стандартного электродного потенциала?
7. Какие типы электродов Вы знаете?
8. Какие типы гальванических элементов Вы знаете?
9. Что такое ЭДС?
10. Как рассчитывается максимальная электрическая работа, которую может произвести гальванический элемент?
11. Как рассчитывается изменение термодинамических функций DG0, DH0, DS0 и константа равновесия реакции, протекающей в замкнутом гальваническом элементе.
12. Какую величину называют электрической проводимостью раствора? В каких единицах измеряется эта величина?
13. От каких факторов зависит электрическая проводимость растворов электролитов?
14. Что характеризует удельная электрическая проводимость? Как можно определить эту величину?
15. Как зависит удельная электрическая проводимость от концентрации сильного электролита? Ответ аргументируйте.
16. Как зависит удельная электрическая проводимость от концентрации слабого электролита? Ответ аргументируйте.
17. Какую величину называют молярной электрической проводимостью раствора? Как эта величина зависит от концентрации раствора сильного и слабого электролита?
|
|
|
18. Что понимают под предельной молярной электрической проводимостью раствора? Как можно определить эту величину для сильных и слабых электролитов?
19. Как определить степень и константу диссоциации слабого электролита, измеряя электрическую проводимость раствора?
20. Как определить произведение растворимости трудно растворимого соединения, измеряя электрическую проводимость раствора?
Таблица 3. 5 – Варианты заданий
| Вари-ант | Электролит А | Подвариант | |||||||||||
| с× 103, моль/л | r× 10-2, Ом× м | с× 103, моль/л | r× 10-2, Ом× м | с× 103, моль/л | r× 10-2, Ом× м | с× 103, моль/л | r× 10-2, Ом× м | с× 103, моль/л | r× 10-2, Ом× м | с× 103, моль/л | r× 10-2, Ом× м | ||
| Изомасляная кислота* | 1, 00 | 2, 370 | 1, 47 | 1, 934 | 1, 67 | 1, 805 | 2, 00 | 1, 639 | 3, 85 | 1, 120 | 7, 14 | 0, 844 | |
| Масляная кислота | 1, 04 | 2, 278 | 1, 35 | 1, 976 | 1, 72 | 1, 736 | 2, 38 | 1, 464 | 2, 78 | 1, 357 | 4, 55 | 1, 042 | |
| Муравьиная кислота | 1, 11 | 0, 655 | 1, 39 | 0, 569 | 1, 85 | 0, 483 | 2, 27 | 0, 432 | 3, 13 | 0, 359 | 4, 17 | 0, 307 | |
| Пропионовая кислота | 1, 22 | 2, 174 | 1, 51 | 1, 919 | 1, 92 | 1, 712 | 2, 63 | 1, 451 | 5, 56 | 0, 988 | 1, 61 | 1, 873 | |
| Уксусная кислота | 1, 67 | 1, 563 | 1, 00 | 2, 062 | 1, 47 | 1, 672 | 3, 85 | 1, 018 | 7, 14 | 2, 924 | 2, 00 | 1, 433 | |
| Гидроксид аммония | 4, 00 | 1, 381 | 5, 56 | 1, 136 | 9, 09 | 0, 880 | 16, 67 | 0, 652 | 7, 14 | 0, 993 | 5, 00 | 1, 205 | |
| Гидроксид аммония | 4, 20 | 1, 337 | 5, 10 | 1, 188 | 6, 25 | 1, 066 | 12, 50 | 0, 751 | 20, 00 | 0, 595 | 11, 76 | 0, 773 | |
| Уксусная кислота | 1, 35 | 1, 748 | 1, 72 | 1, 546 | 1, 04 | 2, 020 | 4, 55 | 0, 935 | 2, 38 | 1, 309 | 2, 78 | 1, 170 | |
| Пропионовая кислота | 1, 04 | 2, 387 | 1, 35 | 2, 058 | 1, 72 | 1, 805 | 2, 38 | 1, 534 | 4, 55 | 1, 093 | 2, 78 | 1, 416 | |
| Муравьиная кислота | 1, 25 | 0, 606 | 1, 56 | 0, 532 | 2, 50 | 0, 408 | 3, 57 | 0, 333 | 5, 00 | 0, 278 | 6, 25 | 0, 246 | |
| Масляная кислота | 1, 00 | 2, 331 | 1, 47 | 1, 890 | 1, 67 | 1, 761 | 2, 00 | 1, 603 | 3, 85 | 1, 134 | 7, 14 | 0, 819 | |
| Изомасляная кислота* | 1, 04 | 2, 326 | 1, 35 | 2, 024 | 1, 72 | 1, 779 | 2, 38 | 1, 495 | 2, 78 | 1, 377 | 4, 55 | 1, 089 | |
| Изомасляная кислота* | 1, 11 | 2, 242 | 1, 39 | 1, 992 | 1, 85 | 1, 709 | 2, 27 | 1, 536 | 3, 13 | 1, 294 | 4, 17 | 1, 116 | |
| Масляная кислота | 1, 25 | 2, 058 | 1, 56 | 1, 825 | 2, 50 | 1, 429 | 3, 13 | 1, 267 | 3, 57 | 1, 182 | 6, 25 | 0, 879 | |
| Муравьиная кислота | 1, 00 | 0, 704 | 1, 47 | 0, 552 | 1, 67 | 0, 513 | 2, 00 | 0, 463 | 3, 85 | 0, 321 | 7, 14 | 0, 228 | |
| Пропионовая кислота | 1, 39 | 2, 020 | 1, 11 | 2, 299 | 2, 27 | 1, 567 | 1, 85 | 1, 742 | 4, 17 | 1, 142 | 3, 13 | 1, 326 | |
| Уксусная кислота | 1, 56 | 1, 623 | 2, 50 | 1, 274 | 1, 25 | 1, 818 | 5, 00 | 0, 889 | 3, 57 | 1, 062 | 6, 25 | 0, 796 | |
| Гидроксид аммония | 4, 40 | 1, 299 | 5, 88 | 1, 098 | 8, 33 | 0, 917 | 15, 38 | 0, 678 | 6, 67 | 1, 020 | 10, 00 | 0, 840 | |
| Гидроксид аммония | 4, 60 | 1, 264 | 7, 69 | 0, 956 | 11, 11 | 0, 797 | 14, 29 | 0, 707 | 25, 00 | 0, 533 | 4, 83 | 1, 229 | |
| Уксусная кислота | 1, 51 | 1, 513 | 1, 92 | 1, 462 | 1, 22 | 1, 845 | 1, 61 | 1, 597 | 2, 63 | 1, 241 | 5, 56 | 0, 845 | |
| Пропионовая кислота | 1, 47 | 1, 961 | 1, 00 | 2, 439 | 2, 00 | 1, 678 | 1, 67 | 1, 838 | 7, 14 | 0, 870 | 3, 85 | 1, 192 | |
| Муравьиная кислота | 1, 22 | 0, 616 | 1, 51 | 0, 539 | 1, 92 | 0, 473 | 2, 63 | 0, 396 | 5, 56 | 0, 261 | 1, 61 | 0, 522 | |
| Масляная кислота | 1, 51 | 1, 848 | 1, 92 | 1, 637 | 1, 22 | 2, 079 | 5, 56 | 0, 942 | 1, 61 | 1, 802 | 2, 63 | 1, 393 | |
| Масляная кислота | 1, 11 | 2, 198 | 1, 39 | 1, 946 | 1, 85 | 1, 669 | 2, 27 | 1, 504 | 4, 17 | 1, 091 | 5, 00 | 0, 990 | |
| Изомасляная кислота* | 1, 25 | 2, 105 | 1, 56 | 1, 873 | 2, 50 | 1, 460 | 3, 57 | 1, 111 | 5, 00 | 1, 015 | 6, 25 | 0, 904 | |
| Изомасляная кислота* | 1, 22 | 2, 137 | 1, 51 | 1, 901 | 1, 92 | 1, 675 | 2, 63 | 1, 418 | 5, 56 | 0, 962 | 1, 61 | 1, 842 | |
|
|
|
4 МЕТОДЫ ОПРЕДЕЛЕНИЯ СТРОЕНИЯ ВЕЩЕСТВА
4. 1 Электрические свойства молекул
Все изменения, происходящие с молекулой в электрическом поле, принято называть поляризацией. Количественную характеристику свойства молекулы поляризоваться называют поляризуемостью. Полярная молекула характеризуется дипольным моментом m, величина которого выражается в единицах Дебая (Д), или в Кл× м. 1Д = 3. 336× 10-30 Кл× м. Если молекула неполярная μ = 0.
При помещении неполярной молекулы в электрическое поле происходит деформация молекулы: смещение отрицательных (электронов) и положительных (ядерной плотности) зарядов друг относительно друга, в результате чего молекула приобретает индуцированный(наведенный) дипольный моментμ инд, величина которого зависит от напряженности электрического поля Е:
|
|
|
, (4. 1)
где e0 – диэлектрическая проницаемость вакуума.
Коэффициент пропорциональности 
называют поляризуемостью молекулы, размерность 
– м3 (см3). Эта величина складывается из поляризуемости ядерной плотности 
и поляризуемости электронного облака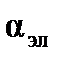 
, т. е. 
, причем 
. Поляризуемоcть молекулы в первом приближении характеризует ее размер в системе СИ:
, (4. 2)
где r – эффективный радиус молекулы, м.
Полярная же молекула вследствие существования собственного дипольного момента при попадании в электрическое поле стремиться ориентироваться вдоль направления поля. Кроме того, в ней, как и в неполярной молекуле, возникает наведенный дипольный момент. В этом и заключается поляризация молекул.
В общем случае полная поляризуемость одного моля молекул в 1м3 ( молярная поляризуемость Рm) складывается из поляризуемости ориентации, поляризуемости электронного облака и поляризуемости атомных ядер:
, (4. 3)
где e – относительная диэлектрическая проницаемость;
e0 – диэлектрическая проницаемость вакуума 8, 854× 10-12 Ф/м;
М – молярная масса вещества;
r – его плотность;
NA – постоянная Авагадро, равная 6, 02× 1023моль-1;
k – постоянная Больцмана, равная 1, 38× 10-23 Дж/К.
Молярная поляризуемость Рm имеет размерность молярного объема (м3/моль или см3/моль). Уравнение (4. 3) носит название уравнения Дебая и справедливо в постоянном (статическом) электрическом поле для газообразных веществ.
Для неполярных молекул уравнение Дебая переходит в уравнение Клаузиуса-Мосотти:
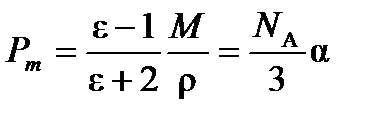(4. 4)
|
|
|
Уравнение Дебая можно записать в виде:
, (4. 5)
где 
и 
.
Таким образом, зная величины молярной поляризуемости при двух температурах, можно вычислить дипольный момент газовой молекулы и поляризуемость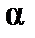 
, а, следовательно, и эффективный радиус молекулы.
Пример: Молярная поляризуемость ацетона в газообразном состоянии составляет при 0оС 183. 8× 10-6 м3/моль, а при 30 оС 167. 2× 10-6 м3/моль. Вычислим дипольный момент и эффективный радиус молекулы.
Решение:
Из температурной зависимости молярной поляризуемости можно вычислить коэффициент В в уравнении (4. 5)
м3× К/моль
Тогда 
Кл× м
Используя значение молярной поляризуемости при данной температуре и вычисленную величину В, легко определить параметр А иполяризуемость 
:
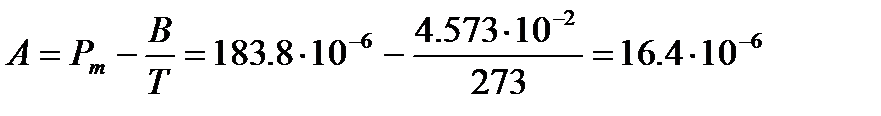м3/моль
м3
Следовательно, эффективный радиус молекулы, рассчитанный по уравнению (4. 2), равен
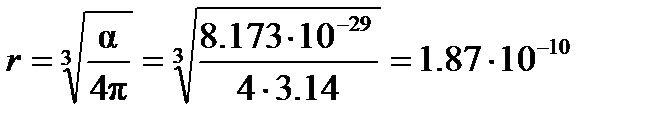м.
Поляризуемость молекулы зависит от частоты внешнего поля. Если частота поля n ~ 1010 Гц, то полярные молекулы не успевают ориентироваться вдоль направления поля, и ориентационная составляющая поляризуемости исчезает. При n > 1013 Гц остается только электронная составляющая поляризуемости. При оптических частотах имеется простое соотношение между относительной диэлектрической проницаемостью при частоте n и показателем преломления n: en = n2n. Тогда
(4. 6)
Молярную поляризуемость при оптических частотах называют молярной рефракцией R. Только рефракцию можно определить как отдельный вид поляризуемости. Показатель преломления зависит от длины волны падающего света. Обычно определяют показатель преломления при строго определенной длине волны, соответствующей D-линии спектра желтого натриевого пламени (l = 589. 3 нм) –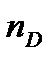 
. Таким образом, молярную рефракцию можно определить, измеряя показатель преломления и плотность вещества по формуле Лоренц –Лорентца:
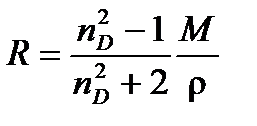(4. 7)
Размерность молярной рефракции, естественно, такая же, как и у молярной поляризуемости, м3/моль (см3/моль).
Экспериментально установлено, что молярная рефракция молекулы приближенно является суммой рефракций отдельных атомов, ионов или связей, входящих в нее. Для вычисления молярной рефракции по аддитивной схеме наиболее часто используют систему атомных, групповых рефракций и инкрементов Ф. Эйзенлора (КС, таблица 91, с. 156).
|
|
|
Пример: По экспериментальным данным и правилу аддитивности определим молярную рефракцию, вычислим электронную поляризуемость, дипольный момент и эффективный радиус молекулы ацетона, если молярная поляризуемость ацетона при 293К составляет 173× 10-6 м3/моль, показатель преломления n=1. 3591 и плотность r=0. 7905× 103 кг/м3.
Решение:
Молярная рефракция ацетона, вычисленная по правилу аддитивности, представляет собой сумму рефракций атомов углерода, водорода и кислорода, входящего в карбонильную группу. Используя значения атомных рефракций из таблицы 91 [КС], находим
м3/моль.
Величина молярной рефракции, рассчитанная по уравнению (4. 7) с использованием экспериментальных данных, составляет
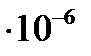м3/моль.
Так как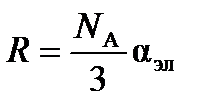 
, то электронная составляющая поляризуемости равна
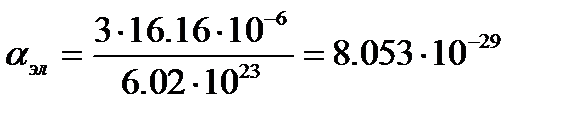м3.
Пренебрегая малой величиной 
, можно считать 
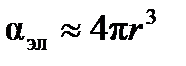и рассчитать величину радиуса молекулы ацетона
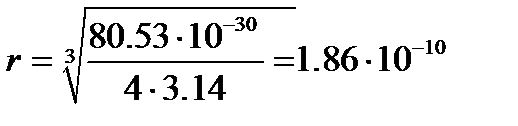м.
Приближенно можно записать, что
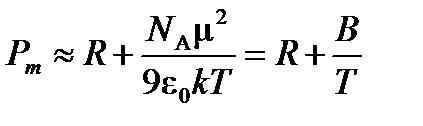
Тогда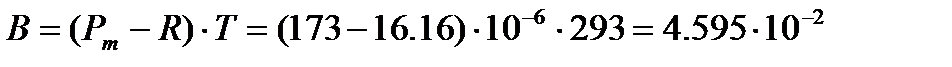 
м3× К/моль, и дипольный момент молекулы ацетона
Кл× м.
Используя свойство аддитивности молярной рефракции, можно решить вопрос о возможном строении молекул.
Пример: Элементарный состав органического соединения: С – 54. 5%; O – 36. 4%; Н – 9. 1% (масс. ). Молярная масса 88× 10-3 кг/моль. Показатель преломления и плотность соответственно равны: n = 1. 398, r = 0. 955× 103 кг/м3. Определим структурную формулу соединения.
Решение:
Определим количества атомов С, О и Н в соединении:
С: 
; О: 
; Н: 
.
Следовательно, формула соединения С4Н8О2.
Для данного соединения возможны несколько структурных формул.
Например: кислота − СН3-СН2-СН2-СООН; непредельный двухатомный спирт - СН2=СН-СН2СН(ОН)2 и эфир СН3-СН2- СООСН3.
Для 1-го соединения величина молярной рефракции, вычисленная по правилу аддитивности, складывается из рефракций атомов углерода, рефракций атомов водорода и рефракций атома кислорода, входящего в карбонильную группу, и атома кислорода, входящего в гидроксильную группу:
R1 = (4× 2. 418 + 8× 1. 1 + 2. 211 + 1. 525) × 10-6 = 22. 208× 10-6 м3/моль.
Для 2-го соединения величина молярной рефракции представляет собой сумму рефракций атомов углерода, рефракций атомов водорода, рефракций атомов кислорода, входящих в гидроксильную группу, и рефракцию двойной связи:
R2 = (4× 2. 418 + 8× 1. 1 + 2× 1. 525 + 1. 733) × 10-6 = 23. 255× 10-6 м3/моль.
Для расчета молярной рефракции 3-го соединения суммируем рефракции атомов углерода, водорода и рефракцию атомов кислорода, входящего в карбонильную группу, и кислорода, входящего в эфирную группу:
R3 = (4× 2. 418 + 8× 1. 1 + 2. 211 + 1. 643) × 10-6 = 22. 326× 10-6 м3/моль.
Величина молярной рефракции, вычисленная по экспериментальным данным, составляет:
Rэксп =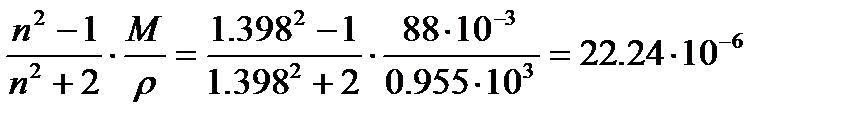 
м3/моль.
Наилучшее совпадение Rэксп c R1. Следовательно, структурная формула соединения СН3-СН2-СН2-СООН.
На практике часто пользуются удельной рефракцией r, т. е. рефракцией единицы массы вещества
(4. 8)
Размерность r – м3/кг или см3/г. Подобно молярной, удельная рефракция смеси тоже аддитивна: удельная рефракция смеси равна сумме удельных рефракций составляющих смесь веществ, умноженных на массовую долю вещества в смеси.
Для двухкомпонентного раствора можно записать:
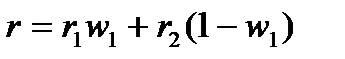, (4. 9)
где r – удельная рефракция раствора;
r1 и r2 – удельные рефракции компонентов раствора;
w1 – массовая доля первого компонента в растворе.
Соотношение (4. 9) часто используют для определения количественного состава двухкомпонентной смеси.
Пример: Найдем процентное содержание бензола в смеси с нитробензолом, если удельная рефракция смеси равна 0. 287× 10-3 м3/кг. Плотность и показатель преломления при 20оС соответственно равны: бензола – 0. 879× 103 кг/м3 и 1. 5011; нитробензола – 1. 2033× 103 кг/м3 и 1. 5524.
Решение:
Удельная рефракция бензола, вычисленная по уравнению (4. 8), равна
м3/кг,
а удельная рефракция нитробензола
м3/кг
Тогда массовая доля бензола, рассчитанная по (4. 9), составит
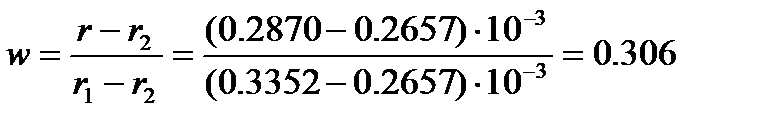
Состав смеси: 30. 6% бензола и 69. 4% нитробензола.
|
|
|
