 |
4.2.6 Многовариантное задание №12 «Колебательные спектры двухатомных молекул»
|
|
|
|
Решение.
Подставим в уравнение (4. 65) для основного тона 
| (4. 75) |
для первого обертона 
| (4. 76) |
для второго обертона 
| (4. 77) |
Пример: В инфракрасном спектре поглощения двухатомной молекулы определены положения двух первых самых сильных линий 3962 и 7743 см-1. Найдите волновое число собственных колебаний, коэффициент ангармоничности и ангармоничность молекулы.
Решение.
Первая линия отвечает основному тону (уравнение (4. 75)), вторая – первому обертону (уравнение (4. 76)). Составим и решим систему уравнений:
Домножим первое уравнение на 3:
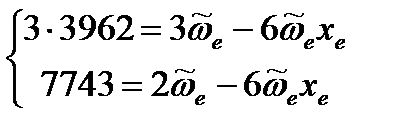
Вычтем из первого уравнения второе:
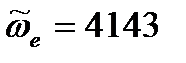см-1
Подставим полученное значение, например, в первое уравнение (уравнение для основного тона) и вычислим ангармоничность и далее коэффициент ангармоничности:
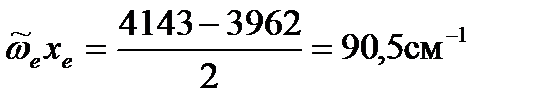
Пример: В колебательном спектре молекулы CO в свободном состоянии и в случаях, когда CO адсорбирована на поверхности металлов определены волновые числа основной полосы поглощения. Волновое число собственных колебаниий CO в свободном неадсорбированном состоянии 2169 см-1. Считая коэффициент ангармоничности во всех случаях одним и тем же, рассчитайте волновые числа собственных колебаний CO, энергию и силовую постоянную связи C=O во всех случаях. Сделайте вывод о характере адсорбции.
| Молекула | Основная полоса поглощения, см-1 |
| CO | |
| CO, адсорбированная на Cu | |
| CO, адсорбированная на Pt | |
| CO, адсорбированная на Pd | |
| CO, адсорбированная на Ni |
Решение.
Основной полосе CO или основному тону отвечает уравнение (4. 75). Используем данные для молекулы CO в свободном состоянии 
для нахождения коэффициента ангармоничности:
|
|
|
Преобразуем уравнение (4. 75) относительно 
и рассчитаем волновые числа собственных колебаний для молекул CO, адсорбированных на металлах:
Cu:
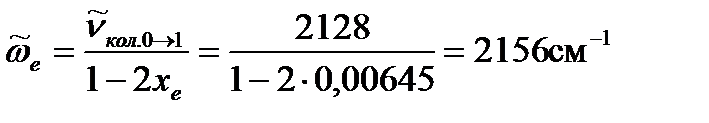
Pt:
Pd:
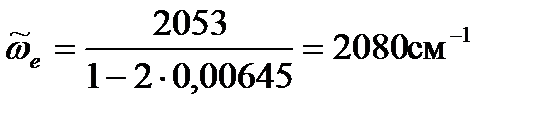
Ni:
Энергия связи в молекуле противоположна по физическому смыслу энергии диссоциации. Используем для ее оценки, например, уравнение (4. 71):
CO:
Дж
или
Дж/моль
Энергии диссоциации для молекул CO, адсорбированных на металлах, оцениваем аналогично:
Cu:
Дж
или
Дж/моль.
Pt:
Дж
или
Дж/моль.
Pd:
Дж
или
Дж/моль.
Наконец, Ni:
Дж
или
Дж/моль.
Для нахождения силовой постоянной перепишем уравнение (4. 57):
| (4. 78) |
Вначале оценим приведенную массу молекулы CO:
, где массы ядер углерода 
и кислорода 
(в граммах).
Затем рассчитаем силовые постоянные:
для свободной CO:
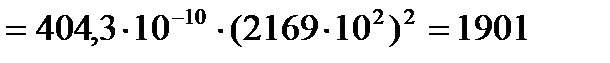кг/с2
и для адсорбированной на металлах молекулы CO:
Cu:
кг/с2
Pt:
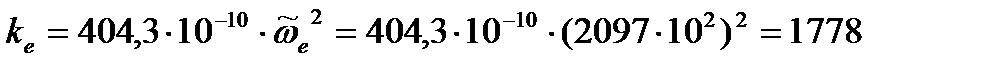кг/с2
Pd:
кг/с2
Ni:
кг/с2
Анализ выполненных вычислений свидетельствует об уменьшении энергии связи и силовой постоянной и, следовательно, об ослаблении связи С=O при адсорбции на металлах.
Пример: Оцените величину и направление изотопного сдвига основной полосы поглощения в колебательном спектре молекулы 13CO, адсорбированной на поверхности меди.
Решение.
Из предыдущего примера возьмем необходимые данные для неизотопозамещенной молекулы CO, адсорбированной на меди:
волновое число собственных колебаний:
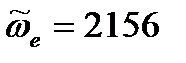см-1,
приведенная масса молекулы CO:
Рассчитаем приведенную массу изотопозамещенной молекулы 13CO:
Предполагая, что силовые постоянные близки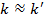 
, оценим по уравнению (4. 74) отношение волновых чисел собственных колебаний и значение 
для изотопозамещенной молекулы:
|
|
|
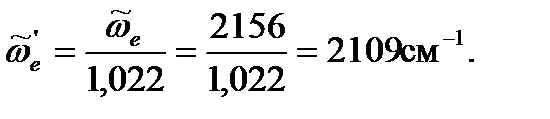
Положение полосы основного тона определим по уравнению (4. 75), позаимствовав из предыдущего примера значение коэффициента ангармоничности и положение полосы основного тона для неизотопозамещенной молекулы CO, адсорбированной на меди:
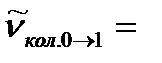2128 см-1.
см-1.
Делаем вывод: изотопный сдвиг в длинноволновую (или низкочастотную) область составляет 2128 - 2082 = 46 см-1.
4. 2. 6 Многовариантное задание №12 «Колебательные спектры двухатомных молекул»
1. Напишите квантово-механическое уравнение для расчета энергии колебательного движения двухатомной молекулы как гармонического осциллятора.
2. Напишите квантово-механическое уравнение для расчета энергии колебательного движения двухатомной молекулы как ангармонического осциллятора.
3. Вычислите по определенным изИК-спектра поглощения двухатомной молекулы A основному тону ( 
), первому обертону ( 
), второму обертону (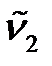 
) или третьему обертону ( 
) (таблица 4. 4) волновое число собственных колебаний 
, коэффициент ангармоничности 
и ангармоничность 
.
4. Вычислите волновые числа пропущенных линий в ИК-спектре поглощения двухатомной молекулы A ( , , 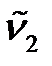или ).
5. Определите энергию колебательного движения молекулы A на нулевом колебательном квантовом уровне E0 (Дж), используя волновое число собственных колебаний и ангармоничность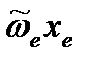 
(см. п. 3)
6. Выведите уравнение для расчета максимального колебательного квантового числа.
7. Определите максимальное колебательное квантовое число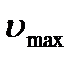 
для молекулы A.
8. Определите энергию колебательного движения 
(Дж) на максимальном колебательном квантовом уровне.
9. Определите энергию диссоциации D0 молекулы A (кДж/моль).
10. Вычертите график зависимости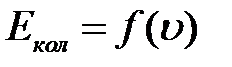 
, выбрав 3-4 значения квантового числа 
и рассчитав значения Eкол. в интервале от 0 до 
.
11. Укажите на графике энергию колебательного движения на максимальном колебательном квантовом уровне Emax (Дж) и энергию диссоциации D0 .
12. Вычислите силовую постоянную химической связи 
двухатомной молекулы A.
13. Вычислите волновое число собственных колебаний изотопозамещенной молекулы B.
|
|
|
14. Определите величину и направление изотопного сдвига для основного тона.
Таблица 4. 4 – Варианты заданий
| Вариант | Молекула А | Под-вариант | 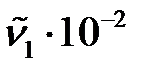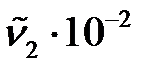 , м-1
|  , м-1
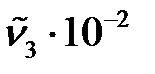|  , м-1
|  , м-1
| Молекула B |
| HI | - | - | 2HI | ||||
| - | - | 3HI | |||||
| - | - | 2H129I | |||||
| - | - | 3H131I | |||||
| - | - | H129I | |||||
| - | - | H131I | |||||
| HF | - | 2HF | |||||
| 3H18F | |||||||
| 2H18F | |||||||
| 3HF | |||||||
| H18F | |||||||
| 2HF | |||||||
| HCl | - | 2HCl | |||||
| 3HCl | |||||||
| H37Cl | |||||||
| 3HCl | |||||||
| 2H37Cl | |||||||
| 3H37Cl | |||||||
| SO | - | S18O | |||||
| 34SO | |||||||
| S17O | |||||||
| 36SO | |||||||
| 33S17O | |||||||
| 33SO | |||||||
| BCl | B37Cl | ||||||
| 10BCl | |||||||
| B37Cl | |||||||
| 10B37Cl | |||||||
| 10BCl | |||||||
| B37Cl | |||||||
| NO | - | N18O | |||||
| N17O | |||||||
| 15N18O | |||||||
| 15NO | |||||||
| 15N17O | |||||||
| 13NO | |||||||
| CaF | Са18F | ||||||
| 43Са18F | |||||||
| 44Са18F | |||||||
| 42СаF | |||||||
| 43СаF | |||||||
| 44СаF |
Продолжение таблицы 4. 4
| Вариант | Молекула А | Под-вариант | 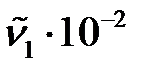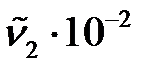, м-1
| , м-1
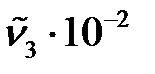| , м-1
| , м-1
| Молекула B |
| HBr | - | 3HBr | |||||
| 2HBr | |||||||
| H77Br | |||||||
| H85Br | |||||||
| H84Br | |||||||
| H82Br | |||||||
| ClI | - | 37ClI | |||||
| 37Cl129I | |||||||
| Cl129I | |||||||
| 37Cl125I | |||||||
| Cl125I | |||||||
| 37ClI | |||||||
| FCl | - | 18FCl | |||||
| F37Cl | |||||||
| 18F37Cl | |||||||
| F37Cl | |||||||
| 18FCl | |||||||
| F37Cl | |||||||
| CO | - | 13CO | |||||
| C17O | |||||||
| 17CO | |||||||
| C18O | |||||||
| 14CO | |||||||
| 15CO | |||||||
| H2H | 3HН | ||||||
| 3H2Н | |||||||
| H3Н | |||||||
| 2HН | |||||||
| 2H2Н | |||||||
| 3H3Н | |||||||
| SH | S2H | ||||||
| 33S2H | |||||||
| 33S3H | |||||||
| 34S2H | |||||||
| 34S3H | |||||||
| S3H | |||||||
| NBr | 13NBr | ||||||
| 15NBr | |||||||
| N79Br | |||||||
| 15N79Br | |||||||
| 13N79Br | |||||||
| N80Br |
|
|
|
Продолжение таблицы 4. 4
| Вариант | Молекула А | Под-вариант | 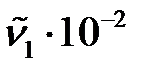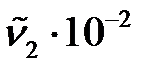, м-1
| , м-1
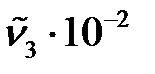| , м-1
| , м-1
| Молекула B |
| NS | S13N | ||||||
| 34SN | |||||||
| S15N | |||||||
| 36SN | |||||||
| 33S15N | |||||||
| 33SN | |||||||
| SiF | Si18F | ||||||
| 30SiF | |||||||
| 29Si18F | |||||||
| 30Si18F | |||||||
| 29SiF | |||||||
| Si18F | |||||||
| OH | - | O2H | |||||
| 17O2H | |||||||
| 17OH | |||||||
| O3H | |||||||
| 18O2H | |||||||
| 18OH | |||||||
| SiN | Si13N | ||||||
| 30SiN | |||||||
| 29Si13N | |||||||
| 30Si15N | |||||||
| 29SiN | |||||||
| Si13N | |||||||
| CP | C30P | ||||||
| 13CP | |||||||
| 13C30P | |||||||
| C30P | |||||||
| 13CP | |||||||
| 13C30P | |||||||
| BeS | Be36S | ||||||
| Be34S | |||||||
| Be33S | |||||||
| 7BeS | |||||||
| 7Be33S | |||||||
| 7Be36S | |||||||
| BeO | Be18O | ||||||
| Be17O | |||||||
| Be18O | |||||||
| 7BeO | |||||||
| 7Be18O | |||||||
| 7Be17O |
|
|
|
Продолжение таблицы 4. 4
| Вариант | Молекула А | Под-вариант | 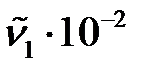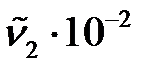, м-1
| , м-1
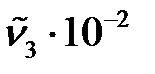| , м-1
| , м-1
| Молекула B |
| BeI | 7BeI | ||||||
| 7Be125I | |||||||
| 7Be129I | |||||||
| 7Be131I | |||||||
| Be125I | |||||||
| Be129I | |||||||
| CN | - | 13C N | |||||
| 13C15N | |||||||
| 14CN | |||||||
| C13N | |||||||
| C15N | |||||||
| 13C13N | |||||||
| Be2H | 7BeH | ||||||
| 7Be3H | |||||||
| BeH | |||||||
| Be3H | |||||||
| 7Be2H | |||||||
| 7BeH | |||||||
| IBr | - | 131IBr | |||||
| 129I80Br | |||||||
| 129I79Br | |||||||
| 125IBr | |||||||
| I79Br | |||||||
| I80Br | |||||||
| BI | 10BI | ||||||
| 10B125I | |||||||
| 10B131I | |||||||
| B125I | |||||||
| B129I | |||||||
| B131I | |||||||
| SiO | Si18O | ||||||
| Si17O | |||||||
| 29Si18O | |||||||
| 30Si17O | |||||||
| 29SiO | |||||||
| 30SiO | |||||||
| SiCl | Si37Cl | ||||||
| 30SiCl | |||||||
| 29Si37Cl | |||||||
| 30Si37Cl | |||||||
| 29SiCl | |||||||
| Si37Cl |
Продолжение таблицы 4. 4
| Вариант | Молекула А | Под-вариант | 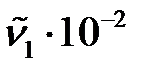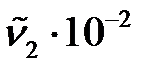, м-1
| , м-1
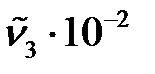| , м-1
| , м-1
| Молекула B |
| PO | P18O | ||||||
| P17O | |||||||
| 30P18O | |||||||
| 30P17O | |||||||
| 30PO | |||||||
| 30PO |
|
|
|
