 |
Применение степенных рядов к приближенным вычислениям
|
|
|
|
Теория рядов имеет большое практическое применение ввиду возможности представления функции f (x) в виде бесконечного ряда более простых функций, в частности, степенного ряда.
а) Разложения, полученные в предыдущем параграфе, позволяют приближенно вычислять частные значения функции.
Пример 15. Вычислим  . Полагая в разложении для функции ex значение x =
. Полагая в разложении для функции ex значение x =  , получим:
, получим:
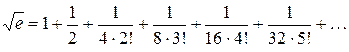
Если отбросить все члены, начиная с шестого, то погрешность вычисления будет меньше 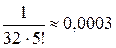 . Отсюда
. Отсюда  » 1,646.
» 1,646.
Пример 16. Вычислить  . Полагая в разложении для
. Полагая в разложении для 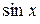 значение x =
значение x =  =0,17(4), получим
=0,17(4), получим
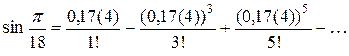
Если отбросить все члены, начиная с третьего, то погрешность будет по абсолютной величине меньше 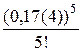 , тогда
, тогда  . Как видно из полученного результата, значение
. Как видно из полученного результата, значение 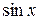 для малых углов сравнимо со значением угла (
для малых углов сравнимо со значением угла (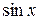 » x).
» x).
б) Используя разложения функций в степенные ряды, можно вычислять определенные интегралы, которые не выражаются через элементарные функции.
Пример 17. Вычислить интеграл 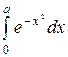 .
.
Разложим подынтегральную функцию в ряд, заменяя в разложении (28) x на - x 2:
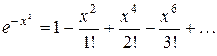
Интегрируя обе части равенства, получим
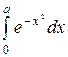 =
= 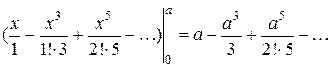
При a = 1 погрешность вычисления интеграла, если отбросить все члены ряда, начиная с четвертого, составит по абсолютной величине  .
.
в) Интегрирование дифференциальных уравнений с помощью рядов используется тогда, когда непосредственное интегрирование дифференциального уравнения невозможно. В таких случаях прибегают к приближенному методу - представлению решения уравнения в виде суммы конечного числа членов ряда Тейлора или Маклорена. Разберем сказанное на примере.
Пример 18. Найти решение уравнения  , удовлетворяющего начальному условию y (0) = 0.
, удовлетворяющего начальному условию y (0) = 0.
Найдем значение первой производной при x = 0: 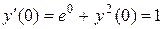 . Продифференцируем исходное уравнение:
. Продифференцируем исходное уравнение:
|
|
|
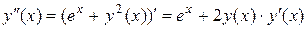 .
.
Найдем значение второй производной при x = 0: 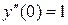 . Этот процесс можно продолжить. Подставляя значения производных в ряд (26¢), получим
. Этот процесс можно продолжить. Подставляя значения производных в ряд (26¢), получим
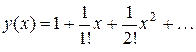
Увеличивая число слагаемых можно получить приближение для y (x) с любой степенью точности.
1) Виды дифференциальных уравнений и методы их решения
| Метод решения | |||
| Дифференциальное уравнение с разделёнными переменными: | 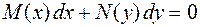
| почленное интегрирование. | |
| Дифференциальное уравнение с разделяющимися переменными | 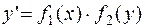
| приведение к уравнению с разделёнными переменными, интегрирование. | |
| Линейное дифференциальное уравнение первого порядка | 
| с помощью подстановки.
 , где , где 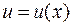 , ,  , ,  сводится к решению двух дифференциальных уравнений первого порядка с разделяющимися переменными.
сводится к решению двух дифференциальных уравнений первого порядка с разделяющимися переменными.
|
| Метод решения | |||
| Уравнение Бернулли | 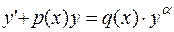 , где , где 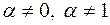
| с помощью подстановки.
 , где , где 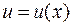 , ,  , ,  сводится к решению двух дифференциальных уравнений первого порядка с разделяющимися переменными.
сводится к решению двух дифференциальных уравнений первого порядка с разделяющимися переменными.
| |
| Однородное дифференциальное уравнение первого порядка | 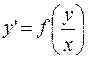
| подстановка.
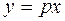 , где , где  , , 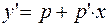
|
2) Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
| Метод решения | ||
| y '' + py ' + qy = 0, где p, q – const | с помощью характеристического уравнения k 2 + pk + q = 0, имеющего корни k 1 и k 2 |
3) Вид общего решения линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами
| Корни характеристического уравнения k 2 + pk + q = 0 | Фундаментальная система решений. | Общее решение уравнения y '' + py ' + qy = 0 |
| 1 k 1 ≠ k 2 – действительные различные числа. |  ; ; 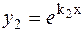
| 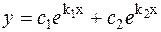
|
| 2 k 1 = k 2 = k – действительные одинаковые числа. | 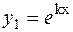 ; ; 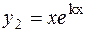
| 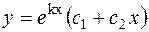
|
3 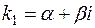 , , 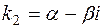 – комплексно-сопряжённые числа,
– комплексно-сопряжённые числа, 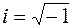
| 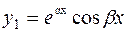 , , 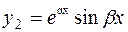
| 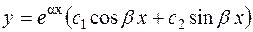
|
4) Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
| Метод решения | ||
| y '' + py ' + q = f (x), где p, q – const | Структура решения:  , где
yоо – общее решение однородного уравнения, соответствующего данному неоднородному;
yчн – некоторое частное решение данного неоднородного уравнения. , где
yоо – общее решение однородного уравнения, соответствующего данному неоднородному;
yчн – некоторое частное решение данного неоднородного уравнения.
|
|
|
|
5) Вид частного решения линейного неоднородного дифференциального уравнения II порядка с постоянными коэффициентами
| Правая часть уравнения | Корни характеристического уравнения | Вид частного решения уравнения yчн |
1. 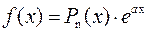
| k 1 ≠ k 2, а ≠ k 1 а ≠ k 2 | 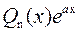
|
| k 1 ≠ k 2, причем а = k 1, а ≠ k 2 или а ≠ k 1, а = k 2 | 
| |
| k 1 = k 2 = α | 
| |
 – многочлен той же степени, что и – многочлен той же степени, что и 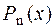 , с неизвестными коэффициентами , с неизвестными коэффициентами
| ||
2  ; а = 0 ; а = 0
| а ≠ k 1, а ≠ k 2 | 
|
| а = k 1, а ≠ k 2 или а ≠ k 1, а = k 2 | 
| |
3 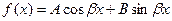 A, B, β– заданные числа A, B, β– заданные числа
| k 1,2 ≠ а ± β i ( 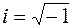 )
а =0 )
а =0
| 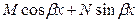 ,
M, N – неизвестные постоянные ,
M, N – неизвестные постоянные
|
k 1,2 = а ± β i ( )
а =0 )
а =0
| 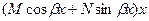 ,
M, N – неизвестные постоянные ,
M, N – неизвестные постоянные
|
| Правая часть уравнения | Корни характеристического уравнения | Вид частного решения уравнения yчн | |
4 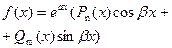 где
где 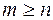 а
а 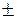 β i -комплексные числа, составленные по виду правой части исходного дифференциального уравнения. β i -комплексные числа, составленные по виду правой части исходного дифференциального уравнения.
|
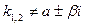
|

| |
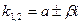
| 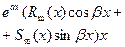
| ||
 – многочлены одной и той же степени m с неизвестными различными коэффициентами. – многочлены одной и той же степени m с неизвестными различными коэффициентами.
| |||
Задание. Найти частное 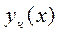 решение дифференциального уравнения
решение дифференциального уравнения 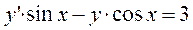 , удовлетворяющее начальному условию:
, удовлетворяющее начальному условию: 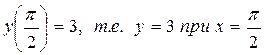
Решение
1) Разделим обе части уравнения на 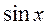
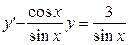 - линейное неоднородное дифференциальное уравнение первого порядка, общий вид которого
- линейное неоднородное дифференциальное уравнение первого порядка, общий вид которого 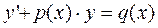
Общее решение данного уравнения найдем в виде 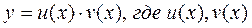 - неизвестные дифференцируемые функции которые надо найти.
- неизвестные дифференцируемые функции которые надо найти.
2) 
 , получаем уравнение:
, получаем уравнение:
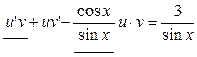 ;
; 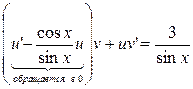
 (*)
(*)
3) Найдем какую-нибудь функцию u, для которой выполняется равенство  - дифференциальное уравнение первого порядка с разделяющимися переменными.
- дифференциальное уравнение первого порядка с разделяющимися переменными. 
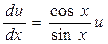 , разделим переменные
, разделим переменные 
Найдем неопределенные интегралы от обеих частей равенства:
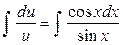
 , так как
, так как 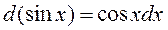
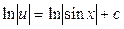 , полагаем с =0 (так как надо найти одну из функций u). Следовательно
, полагаем с =0 (так как надо найти одну из функций u). Следовательно 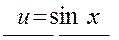
4) Подставим 
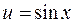 в уравнение
в уравнение 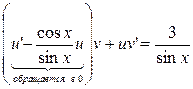
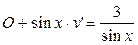 ;
; 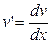 ;
; 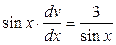 - разделим переменные
- разделим переменные
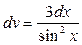 , интегрируем обе части равенства:
, интегрируем обе части равенства: 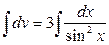
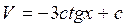
Общее решение данного дифференциального уравнения имеет вид:
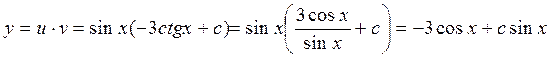 .
.
Итак, 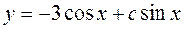
5) Для отыскания частного решения необходимо и достаточно определить значения постоянной с по начальному условию, данному в задании.
|
|
|
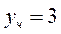 при
при 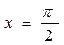 , получаем равенство
, получаем равенство
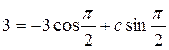 , так как
, так как 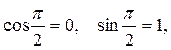 , то
, то 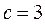 .
.
Следовательно, 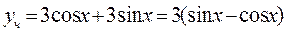
Ответ: 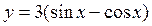
Задание. Найти частное решение дифференциального уравнения второго порядка 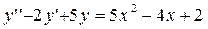 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям 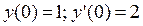
Решение
1) Составим характеристическое уравнение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициента вида (ЛОДУ): 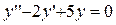
Характеристическое уравнение: 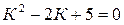
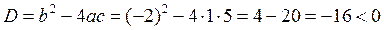
Характеристическое уравнение имеет комплексно-сопряженные корни. 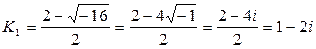
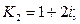
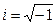 - мнимая единица
- мнимая единица
Общее решение ЛОДУ: 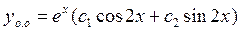
2) Так как правая часть данного линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами (ЛНДУ) имеет вид 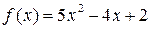 - многочлен второй степени, еах показательная функция отсутствует, то есть а=0 – не является корнем характеристического уравнения, составленного выше, то частное решение ЛНДУ будем искать в виде многочлена второй степени с неизвестными коэффициентами:
- многочлен второй степени, еах показательная функция отсутствует, то есть а=0 – не является корнем характеристического уравнения, составленного выше, то частное решение ЛНДУ будем искать в виде многочлена второй степени с неизвестными коэффициентами:
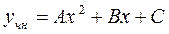

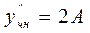
Подставим 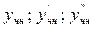 в данное ЛНДУ уравнение:
в данное ЛНДУ уравнение:

Два многочлена равны тогда и только тогда, когда равны коэффициенты при одинаковых степенях x, находим:
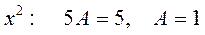
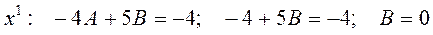
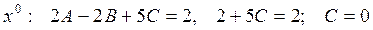
Отсюда  , поэтому общее решение ЛНДУ имеет вид
, поэтому общее решение ЛНДУ имеет вид
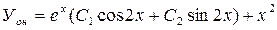
3) Находим частное решение ЛНДУ, удовлетворяющее начальным условиям, данным в задании:

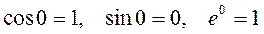
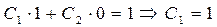
6) Виды дифференциальных уравнений и методы их решения
| Метод решения | |||
| Дифференциальное уравнение с разделёнными переменными: | 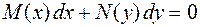
| почленное интегрирование. | |
| Дифференциальное уравнение с разделяющимися переменными | 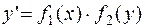
| приведение к уравнению с разделёнными переменными, интегрирование. | |
| Линейное дифференциальное уравнение первого порядка | 
| с помощью подстановки.
 , где , где 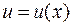 , ,  , ,  сводится к решению двух дифференциальных уравнений первого порядка с разделяющимися переменными.
сводится к решению двух дифференциальных уравнений первого порядка с разделяющимися переменными.
|
| Метод решения | |||
| Уравнение Бернулли | 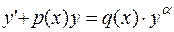 , где , где 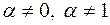
| с помощью подстановки.
 , где , где 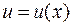 , ,  , ,  сводится к решению двух дифференциальных уравнений первого порядка с разделяющимися переменными.
сводится к решению двух дифференциальных уравнений первого порядка с разделяющимися переменными.
| |
| Однородное дифференциальное уравнение первого порядка | 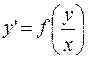
| подстановка.
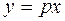 , где , где  , , 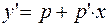
|
|
|
|
7) Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
| Метод решения | ||
| y '' + py ' + qy = 0, где p, q – const | с помощью характеристического уравнения k 2 + pk + q = 0, имеющего корни k 1 и k 2 |
8) Вид общего решения линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами
| Корни характеристического уравнения k 2 + pk + q = 0 | Фундаментальная система решений. | Общее решение уравнения y '' + py ' + qy = 0 |
| 1 k 1 ≠ k 2 – действительные различные числа. |  ; ; 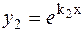
| 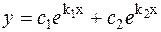
|
| 2 k 1 = k 2 = k – действительные одинаковые числа. | 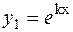 ; ; 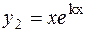
| 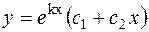
|
3 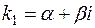 , , 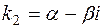 – комплексно-сопряжённые числа,
– комплексно-сопряжённые числа, 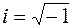
| 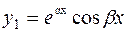 , , 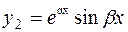
| 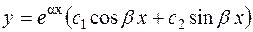
|
9) Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
| Метод решения | ||
| y '' + py ' + q = f (x), где p, q – const | Структура решения:  , где
yоо – общее решение однородного уравнения, соответствующего данному неоднородному;
yчн – некоторое частное решение данного неоднородного уравнения. , где
yоо – общее решение однородного уравнения, соответствующего данному неоднородному;
yчн – некоторое частное решение данного неоднородного уравнения.
|
10) Вид частного решения линейного неоднородного дифференциального уравнения II порядка с постоянными коэффициентами
| Правая часть уравнения | Корни характеристического уравнения | Вид частного решения уравнения yчн |
1. 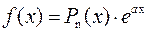
| k 1 ≠ k 2, а ≠ k 1 а ≠ k 2 | 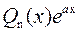
|
| k 1 ≠ k 2, причем а = k 1, а ≠ k 2 или а ≠ k 1, а = k 2 | 
| |
| k 1 = k 2 = α | 
| |
 – многочлен той же степени, что и – многочлен той же степени, что и 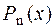 , с неизвестными коэффициентами , с неизвестными коэффициентами
| ||
2  ; а = 0 ; а = 0
| а ≠ k 1, а ≠ k 2 | 
|
| а = k 1, а ≠ k 2 или а ≠ k 1, а = k 2 | 
| |
3 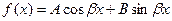 A, B, β– заданные числа A, B, β– заданные числа
| k 1,2 ≠ а ± β i ( 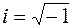 )
а =0 )
а =0
| 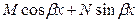 ,
M, N – неизвестные постоянные ,
M, N – неизвестные постоянные
|
k 1,2 = а ± β i ( )
а =0 )
а =0
| 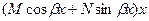 ,
M, N – неизвестные постоянные ,
M, N – неизвестные постоянные
|
| Правая часть уравнения | Корни характеристического уравнения | Вид частного решения уравнения yчн | |
4 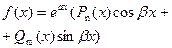 где
где 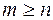 а
а 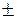 β i -комплексные числа, составленные по виду правой части исходного дифференциального уравнения. β i -комплексные числа, составленные по виду правой части исходного дифференциального уравнения.
|
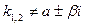
|

| |
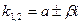
| 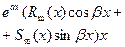
| ||
 – многочлены одной и той же степени m с неизвестными различными коэффициентами. – многочлены одной и той же степени m с неизвестными различными коэффициентами.
| |||
Задание. Найти частное 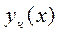 решение дифференциального уравнения
решение дифференциального уравнения 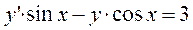 , удовлетворяющее начальному условию:
, удовлетворяющее начальному условию: 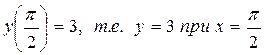
Решение
2) Разделим обе части уравнения на 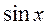
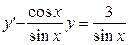 - линейное неоднородное дифференциальное уравнение первого порядка, общий вид которого
- линейное неоднородное дифференциальное уравнение первого порядка, общий вид которого 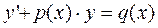
Общее решение данного уравнения найдем в виде 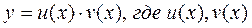 - неизвестные дифференцируемые функции которые надо найти.
- неизвестные дифференцируемые функции которые надо найти.
2) 
 , получаем уравнение:
, получаем уравнение:
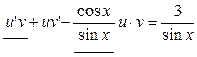 ;
; 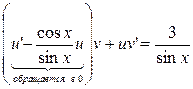
 (*)
(*)
3) Найдем какую-нибудь функцию u, для которой выполняется равенство  - дифференциальное уравнение первого порядка с разделяющимися переменными.
- дифференциальное уравнение первого порядка с разделяющимися переменными. 
|
|
|
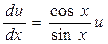 , разделим переменные
, разделим переменные 
Найдем неопределенные интегралы от обеих частей равенства:
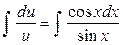
 , так как
, так как 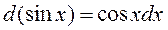
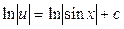 , полагаем с =0 (так как надо найти одну из функций u). Следовательно
, полагаем с =0 (так как надо найти одну из функций u). Следовательно 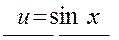
4) Подставим 
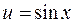 в уравнение
в уравнение 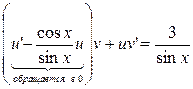
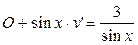 ;
; 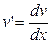 ;
; 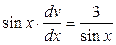 - разделим переменные
- разделим переменные
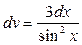 , интегрируем обе части равенства:
, интегрируем обе части равенства: 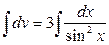
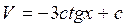
Общее решение данного дифференциального уравнения имеет вид:
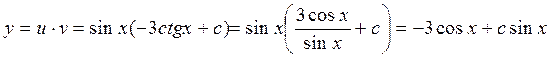 .
.
Итак, 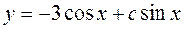
5) Для отыскания частного решения необходимо и достаточно определить значения постоянной с по начальному условию, данному в задании.
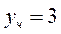 при
при 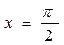 , получаем равенство
, получаем равенство
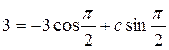 , так как
, так как 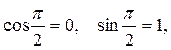 , то
, то 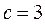 .
.
Следовательно, 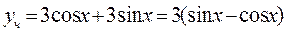
Ответ: 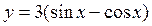
Задание. Найти частное решение дифференциального уравнения второго порядка 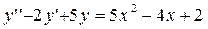 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям 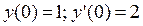
Решение
2) Составим характеристическое уравнение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициента вида (ЛОДУ): 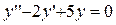
Характеристическое уравнение: 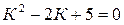
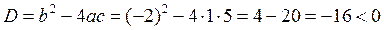
Характеристическое уравнение имеет комплексно-сопряженные корни. 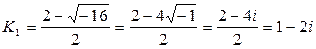
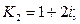
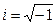 - мнимая единица
- мнимая единица
Общее решение ЛОДУ: 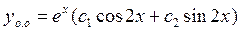
2) Так как правая часть данного линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами (ЛНДУ) имеет вид 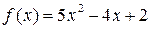 - многочлен второй степени, еах показательная функция отсутствует, то есть а=0 – не является корнем характеристического уравнения, составленного выше, то частное решение ЛНДУ будем искать в виде многочлена второй степени с неизвестными коэффициентами:
- многочлен второй степени, еах показательная функция отсутствует, то есть а=0 – не является корнем характеристического уравнения, составленного выше, то частное решение ЛНДУ будем искать в виде многочлена второй степени с неизвестными коэффициентами:
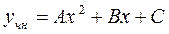

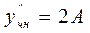
Подставим 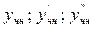 в данное ЛНДУ уравнение:
в данное ЛНДУ уравнение:

Два многочлена равны тогда и только тогда, когда равны коэффициенты при одинаковых степенях x, находим:
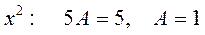
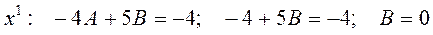
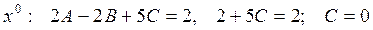
Отсюда  , поэтому общее решение ЛНДУ имеет вид
, поэтому общее решение ЛНДУ имеет вид
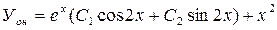
3) Находим частное решение ЛНДУ, удовлетворяющее начальным условиям, данным в задании:

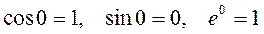
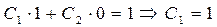
|
|
|


