 |
Системы нелинейных и трансцендентных уравнений
|
|
|
|
При решении систем уравнений они и список переменных задаются как множества, т.е. в фигурных скобках. При этом и результат решения получается в виде множества.
> sys:={x*y=c,x+y=d};
sys:= {x y = c, x + y = d}
>s1:=solve(sys,{x,y});
s1:= {x = -RootOf(_Z - _Z d + c) + d,
2
y = RootOf(_Z - _Z d + c)}
> s2:=allvalues(%);
s2:= {y = 1/2 d + 1/2 %1, x = 1/2 d - 1/2 %1},
{y = 1/2 d - 1/2 %1, x = 1/2 d + 1/2 %1}
2
%1:= sqrt(d - 4 c)
> r1:=s2[1];s2[2];
2
r1:= {y = 1/2 d + 1/2 sqrt(d - 4 c),
2
x = 1/2 d - 1/2 sqrt(d - 4 c)}
2
{y = 1/2 d - 1/2 sqrt(d - 4 c),
2
x = 1/2 d + 1/2 sqrt(d - 4 c)}
Для того чтобы преобразовать его к обычному решению, нужно использовать функцию assign, которая обеспечивает присваивание переменным значений, взятых из множества.
> assign(s2[1]);x;y; # Присвоение первого решения
2
1/2 d - 1/2 sqrt(d - 4 c)
2
1/2 d + 1/2 sqrt(d - 4 c)
> subs(s2[2],sys);expand(%);#Проверка 2-го решения
{d = d,
2 2
(1/2 d - 1/2 sqrt(d - 4 c)) (1/2 d + 1/2 sqrt(d - 4 c)) = c}
{c = c, d = d}
Решение неравенств
Решение неравенств с помощью функции solve осуществляется также, как и уравнений (вместо равенств вводятся неравенства).
> solve(5*x>10,x);
RealRange(Open(2), infinity)
> solve(x^2-2*x-1>0,x);
RealRange(-infinity, Open(1 - sqrt(2))),
RealRange(Open(1 + sqrt(2)), infinity)
> solve({x*y*z>0,y+z>10,x>-1},{x,y,z});
{10 < z, -1 < x, y = 0}, {-1 < x, 10 < y, z = 0}
Решение уравнений в численном виде
Функция solve имеет несколько производных от нее функций. Одна из них:
Fsolve (eqns,vars,options)
- сразу дает решения в форме действительных или комплексных чисел
Некоторые из опций, используемые этой функцией:
complex - находит один или все корни полинома в комплексной форме
maxsols = n - задает нахождение только n корней
interval - задается в виде a..b или x = a..b или {x = a..b, y = c..d} и обеспечивает поиск корней в указанном интервале.
|
|
|
Локализация поика корней позволяет отыскать решения, которые не дают функции solve и fsolve.
> fsolve(sin(x)=0.5);
.5235987756
> fsolve(sin(x)=0.5,x=4..8);
6.806784083
> fsolve(x^5-x,x);
-1., 0, 1.000000000
> fsolve(x^5-x,x,complex);
-1., -1. I, 0, 1. I, 1.000000000
> fsolve(x^5-x,x,complex,maxsols=2);
-1., -1. I
Решение функциональных, рекуррентных и других уравнений. Функция RootOf
Решение функциональных, рекуррентных и др. уравнений
Рекуррентными называются уравнения, у которых решение на заданном шаге находится по одному или нескольким предшествующим шагам. Для решения таких уравнений в Мaple V существует функция rsolve:
Rsolve(eqns,fcns)
eqns - одиночное уравнение или система уравнений
fcns - функция, имя функции или множество имен функций.
> rsolve({y(n)*y(n-1)+y(n)-y(n-1)=0,
>y(0)=a},y);
-------
1 + n a
> rsolve({y(n+1) + f(n) = 2*2^n + n,
> f(n+1) - y(n) = n - 2^n +3,
y(k=1..5)=2^k-1, f(5)=6}, {y, f});
n
{y(n) = 2 - 1, f(n) = n + 1}
Для решения целочисленных уравнений служит функция isolve, для отыскания решений по модулю m функция msolve. Более подробно с работой этих функций можно ознакомиться в справочной системе Maple V.
Решение функционального уравнения, содержащего некоторую функцию f(x) в составе равенства, заключается в нахождении этой функции. Функция solve с указанием f или f(x) в качестве независимой переменной var успешно справляется с этой задачей. Причем указание только имени функции (без переменной) в качестве var приводит к созданию процедуры, и для получения вида найденной функции требуется предпринять дополнительные шаги (например, использовать функцию allvalues или convert).
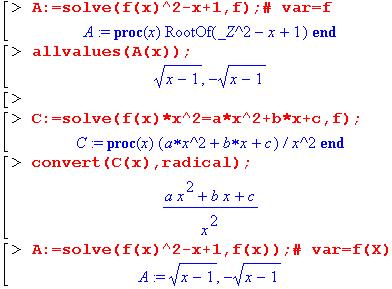
Функция RootOf
В решениях уравнений нередко появляется функция RootOf, означающая, что корни нельзя выразить в радикалах. Эта функция применяется и самостоятельно в виде:
|
|
|
RootOf(expr) или RootOf(expr,x)
где expr -алгебраическое выражение или равенство, имя переменной, относительно которой ищется решение. Если x не указана, ищется универсальное решение по переменной _Z. Когда expr задано не в виде равенства, решается уравнение expr=0. Для получения решений вида RootOf в явном виде может использоваться функция allvalues. Например:
> RootOf(x^3-1,x) mod 7;
3
RootOf(_Z +6)
> allvalues(");
1/3 1/3 1/2 1/3 1/3 1/2 1/3
-6, 1/26,-1/2I3 6,1/26 +1/2I3 6
> evalf(");
-1.817120593,.9085602965-1.573672596I,.9085602965+1.573672596I
Двумерная графика в системе Maple
Команда plot()
Многофункциональная двумерная графическая команда plot() расположена в системной библиотеке Maple, и поэтому доступна в любое время.
С помощью этой команды можно построить график одной или нескольких функций одной вещественной переменной, заданных в явном или параметрическом виде, а также отобразить множество точек в декартовой или полярной системе координат.
Синтаксис команды plot() следующий:
plot(f, h, v,опции); или plot(f, h, v);
f -функция, график которой необходимо отобразить,
h и v представляют, соответственно, диапазон изменения независимой переменной по горизонтальной оси графика и диапазон изменения значения функции вдоль вертикальной оси графика.
Диапазон изменения независимой переменной h задается в виде x=a..b, где a и b -наименьшее и наибольшее значения изменения переменнной,а x -имя независимой переменнной.
Если диапазон не задан, т.е. второй параметр представляет собой просто имя независимой переменной в функции, то по умолчанию принимается следующий интервал ее изменения -10..10. Этот параметр (с диапазоном или нет) обязательно должен присутствовать при задании графика командой plot().
Вертикальный диапазон v, задаваемый третьим параметром, ограничивает вывод графика определенной областью изменения функции. Он необязателен.
Опции определяют вид отображаемого графика: толщину, цвет и тип линии графика, тип осей координат, размещение надписей и т.д. и задаются в форме уравнений имя_опции=значение. Набор возможных опций во всех командах двумерного графического вывода, за некоторым исключением, одинаков.
При отсутствии явного задания опции принимаются их значения по умолчанию.
|
|
|
Ниже в таблице представлены некоторые опции двумерной графики и соответствующие им значения.
| Некоторые опции для двумерной графики: | |
| Опции | Описание |
| color | Задает цвет кривых. |
| coords | Задает тип координатных осей. |
| numpoints | Задает минимальное количество точек графика (по умолчанию numpoints=49). |
| scaling | Задает масштаб графика CONSTRAINED (сжатый) или UNCONSTRAINED (несжатый-по умолчанию). |
| style | Задает стиль построения графика POINT (точечный) или LINE(линиями). |
| title | Задает построение заголовка графика (title="string", где string-строка). |
| titlefont | Определяет шрифт заголовка. |
| labelfont | Определяет шрифт для меток на осях координат. |
| thickness | Определяет толщину линий графиков (0, 1, 2, 3, по умолчанию 0). |
| xtickmarks | Задает минимальное число отметок по оси X. |
| ytickmarks | Задает минимальное число отметок по оси Y. |
| axesfont | Задает шрифт для надписей под засечками вдоль осей координат. Значение этой опции аналогично значению опции FONT. |
| sample | Определяет список значений параметров, который используется для "пробного" отображения кривой. Отключение адаптивного алгоритма вычисления точек кривой позволяет явным образом управлять отображением кривой. |
| legend | Задает отображение легенды для нескольких кривых на одном графике в виде списка, в котором i-й строковый элемент соответствует i-й кривой графика. |
| symbol | Определяет тип символа в пунктах. Его значение может быть любое натуральное число. По умолчанию используются символы раэмером 10 пунктов. Действие этой опции не распространяется на символы POINT. |
Работа с командой plot() не представляет никаких сложностей. Несколько примеров позволяет легко с ней освоиться.
| График функции с надписью: | |

| Первым примером будет отображение графика функции y(x)=x2+sin(x2) на интервале [-4,4] изменения независимой переменной X с созданием надписи. Обратите внимание, что для созднания многострочной надписи в строке значения опции title использован символ перехода на новую строку (\n). Также на графике изменен шрифт надписей вдоль осей, название оси y отображено вертикально. |
| График функции на бесконечном интервале: | |

| Команда plot() может отображать графики функций не только на конечном интервале изменения независимой переменной, но и на бесконечном. |
|
|
|
| Отображение графика параметрически заданной функции: | |

| Не всякую функцию можно представить в явном виде. Многие функции задаются в параметрической форме. Отображение графиков таких функций ничем не отличается от вывода явно задаваемых функций. Единственное отличие заключается в том, что параметрическая кривая задается в виде списка, где первый и второй элементы являются выражениями через параметр, соответственно, горизонтальной и вертикальной координат, а третий элемент списка задает изменение параметра в виде диапазона Maple. Рисунок слева демонстрирует отображение параметрически заданной кривой. |
| Отображение графиков нескольких функций: | |

| Для вывода нескольких функций на одном графике необходимо в команде plot() задавать функции в виде множества или списка, а значение опции color в виде списка позволяет задать цвет для вывода графиков функций. Если опция color не задана, то Maple отображает функции в соответствии со списком цветов по умолчанию. |
При выводе нескольких графиков рекомендуется также отображать легенду заданием списка значений опции legend.
Совет: Легенду всегда можно скрыть или снова отобразить с помощью команды Legend -> ShowLegend.
| Отображение точек на плоскости: | |

| Команда plot() позволяет отображать на графике отдельные точки, которые задаются в виде списка списков, т.е. списка, элементами которого являются списки. Эти двухэлементные списки определяют координаты точек на плоскости. Для вывода точек необходимо задать значение опции style, равной POINT. Если этого не сделать, то Maple отобразит ломаную линию, соединяющую точки в последовательности их задания, не выделяя их специальными символами. В приведенном слева примере точки, заданные своими координатами на плоскости, отображаются с использованием символа ромб symbol=DIAMOND. |
|
|
|


