 |
Анимация двумерных графиков
|
|
|
|
Двумерная анимация создается командой:
animate(y-expr, x= диапазон 1, t= диапазон 2)
Здесь первый параметр y-expr представляет выражение, зависящее от переменной x и параметра t, изменяемых в соответствующих диапазонах.
Для воспроизведения анимационной картинки необходимо выделить график и на появившейся панели инструментов нажать кнопку Начть проигрывание. Можно также воспользоваться командами Play/Stop меню Animation /

Maple 6 позволяет сохранить анимацию в графическом файле формата GIF, который впоследствии можно использовать в HTML-страницах для отображения анимации, т.е. Maple создает, в конечном счете, анимационный GIF-файл. Для этого следует установить графическое устройство gif командой plotsetup() и указать в ней имя файла, в котором будет сохранена анимация:
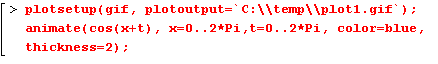

В пространстве анимация создается командой
animate3d(F(x,y,t), x=a..b, y=c..d, t=p..q, опции)
Здесь первый параметр F(x,y,t) представляет выражение от трех переменных или функцию двух первых независимых переменных и параметра t. Остальные параметры задают диапазоны изменения независимых переменных и параметра. Опции задаются в виде уравнений и определяют вид отображаемого анимационного графика.
По умолчанию для представления пространственной анимации создается 8 кадров. Опцией frame всегда можно увеличить их число для получения более плавной картинки смены кадров. Однако следует помнить о времени и памяти, расходуемых на создание большого количества кадров анимации.
Команда animate3d() может одновременно отображать изменение нескольких функций. В этом случае все они должны зависеть от одинаковых независимых переменных и одного и того же параметра и задаваться в виде списка.
Для получения анимационного файла формата GIF следует, как и в случае двумерной анимации, вывести результаты выполнения трехмерной анимации в графическое устройство gif, устанавливаемое командой plotsetup().
|
|
|
Завершая разговор о двумерных графических командах пакета plots, мы позволили себе дать несколько советов относительно отображения функций двух классов: разрывных и быстро осциллирующих.
Как известно, функция может иметь в точке разрывы двух видов: первого рода, когда в этой точке происходит скачок в ее значении,и второго рода, когда значение функции при стремлении независимой переменной к заданной точке стремится к плюс или минус бесконечности. Функции, имеющие разрывы только первого рода, обычно называют кусочно-непрерывными. Простейшим примером такой функции является ступенчатая функция, которая на интервалах непрерывности принимает постоянные значения, а в нескольких точках своей области задания изменяется скачкообразно на некоторую величину. Примером функции с разрывами второго рода является тригонометрический тангенс.
Maple умеет работать с разрывными функциями, имеющими разрывы любого рода. Для задания кусочно-непрерывных функций следует использовать команду piecewise() со следующим синтаксисом:
> pieceewise (условие1,значение1, условие2,значение2,..., условие n,значение n, значение-иначе);
Параметры этой команды идут парами и определяют интервал изменения независимой переменной в виде булева выражения условие n и значение функции на этом интервале значение n, которое является выражением от независимой переменной. Последний параметр значение-иначе определяет вид функции на оставшихся интервалах вещественной оси. Например, чтобы задать функцию f(x) следует выполнить команду:
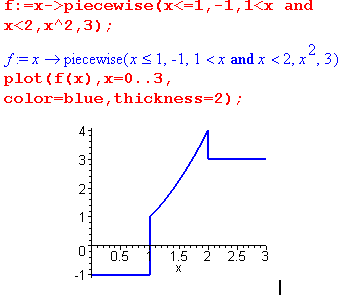
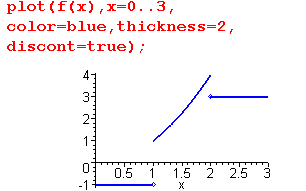
Maple вычерчивает вертикальные линии в точках разрыва, соединяя значения функции справа и слева от точки разрыва. Чтобы избежать такого некорректного отображения разрывной функции, следует при ее вычерчивании устанавливать значение true опции discont:
|
|
|
Графики функций с разрывами второго рода следует строить с обязательным заданием интервала изменения ее значений. Попытка построить график такой функции командой plot() без ограничения на значения функции обречена на провал:
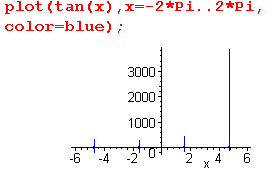
Тогда как ограничения на области изменения значений функции дадут нам правильный график функции с разрывами второго рода:

И здесь опять для удаления из графика функции с разрывами второго рода вертикальных прямых в точках разрыва следует, как и в случае с кусочно-непрерывными функциями, воспользоваться опцией discont:
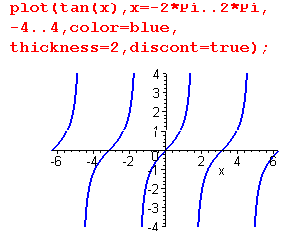
Maple вычерчивает графики функций, вычисляя их значения на некотором множестве равноотстоящих точек независимой переменной. Затем он анализирует изменение функции на полученных интервалах и принимает решение вычислить значения функции в дополнительных точках тех интервалов, где функция является быстро осциллирующей. Однако не во всех случаях этот адаптивный алгоритм срабатывает, и приходится прибегать к явному заданию количества точек на графике, чтобы получить его приемлемое отображение.
Отобразим график быстро осциллирующей функции с использованием только адаптивного алгоритма Maple:
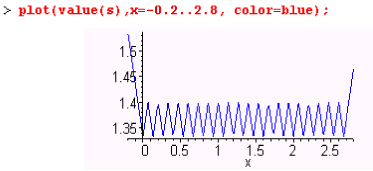
Как видно, зубчики на графике не одинаковой величины, что является свидетельством недостаточности вычисленных адаптивным алгоритмом точек на графике. Улучшить график этой функции поможет задание опции numpoints:

|
|
|


