Двумерные команды пакета plots

На плоскости кроме прямоугольной декартовой системы координат используются и другие.Одной из наиболее часто применяемой является полярная система координат, в которой положение точки задается также двумя велечинами. Они представляют собой длину r радиус-вектора, проведеного из начала координат в заданную точку, и угол наклона "phi" этого вектора относительно положительного направления горизонтальной оси координат.

Многие "замечательные" плоские кривые легче и проще задавать именно в полярной системе координат. Например, окружность радиуса a с центром в начале координат в полярной системе координат задается простым уравнением r=a, тогда как в декартовой системе координат эта же окружность задается уравнением в неявном виде sqrt(x²+y²)=a².

Параметр r - это выражение или функция, зависящая от независимой переменной phi, интерпретируемой как угол поворота радиус-вектора относительно горизонтальной оси. Диапазон изменения независимой перемнной может отсутствовать, тогда используется диапазон изменения по умолчанию -Pi..Pi. Остальные параметры представляют собой такие же опции, что и в функции plot().

Графики функции в полярной системе координат:
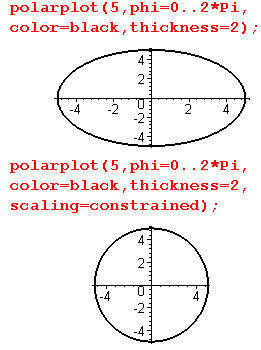
	Для отображения графика функций, заданной в полярной системе координат, в пакете plots существует функция polarplot(). Ее синтаксис похож на синтаксис команды plot() за одним исключением - не задается третий параметр, ограничивающий диапазон изменения значений, в данном случае длины радиус-вектора: polarplot(r, phi=диапазон, опции); С помощью команд интерфейса пользователя или при отображении кривой в соответствующей команде, задав опцию scaling=CONSTRAINED можно исправить дефект изображения окружности.

Если посмотреть на вывод этой команды, то вместо обещанной окружности мы видим эллипс. Дело в том, что по умолчанию во всех графических командах используется значение UNCONSTRAINED параметра scaling. А это означает, что график растягивается по осям таким образом, чтобы полностью заполнить отводимое под него пространство на рабочем листе, что приводит к несоответствию единиц измерения по горизонтальной и вертикальной осям. Подобное явление характерно для вывода всех графических команд Maple.

График параметрически заданой кривой:
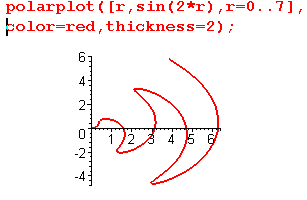
	Команда polarplot() также позваляет отображать графики параметрически заданных кривых. Для этого подобную кривую следует задать в форме трехэлементного списка, в котором первые два элемента представляют выражение через параметр длины радиуса-вектора и его угла поворота, а третий элемент задает диапазон изменения параметра.

Замечание: График этой же функции можно построить и командой plot() ,но следует задать опцию coords=polar.

Замечание: Для отображения командой polarplot() на одном графике нескольких кривых, их следует задавать, как и в случае с командой plot(), в виде списка.

В Maple командой coordplot() млжно начертить "линии уровня" плоских систем координат, поддерживаем командой plot() через опцию coords. В качестве параметра этой функции передается название системы координат (см. опцию coords в таблице опций):

График полярной системы координат.	График биполярной системы координат.

Замечание: Только для полярной системы координат существует специальная команда построения графика функции. Для отображения графиков функций в других допустимых системах координат следует использовать опцию coords команды plot().

Бывает так, что искомая функция, график которой надо отобразить, представляется только в неявном виде f(x,y)=0 и никакими ухищрениями ее нельзя представить в явной форме ни в одной из известных систем координат. Команда implicitplot() разработана для отображения неявных функций:

implicitplot(expr,x=a..b,y=c..d,опции);
implicitplot(f, a..b, c..d,опции);.

График неявно заданной функции:
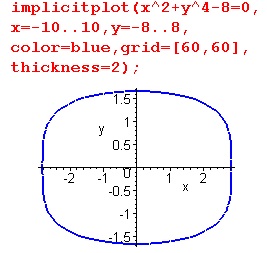
	Здесь в первой форме вызова команды параметр expr представляет уравнение, зависящее от двух переменных x и y, а во второй форме f представляет уравнение, и в левую, и в правую части которого входят только процедуры, функции и операторы от двух переменных. Дополнительно ко всем известным опциям команды plot() можно задать опцию grid=[m,n], определяют сетку из m*n точек, на которой вычерчивается кривая.

При увеличении количества точек в сетке кривая отбражения становится более гладкой без угловых точек. По умолчанию используется сетка 25*25 точек. Опцией coords можно задавать график в равных системах координат, по умолчанию используются декартовая прямоугольная систама координат.

Замечание: Увеличение числа точек в сетке, на которой рассчитывается неявно заданная кривая, приводит к существенному увеличению времени расчета ее графика.

Часто в технике при отображении зависимости двух параметров какой-либо системы используются логарифмические оси координат, т.е. по одной или обеим осям откладываются десятичные логарифмы соответствующих величин. В пакете plots содержатся три команды, позваляющие работать с подобным представлением функций: loglogplot() осуществляет логарифмическое преобразование обеих координат, semilogplot() только горизонтальной оси, а logplot() только вертикальной оси координат.

Отображение функции 10^x в логарифмической шкале:

Очень полезная команда inequal() отображает на плоскости решение смешанной системы линейных неравенств и уравнений двух независимых переменных. Ее синтаксис несколько отличается от синтаксиса большинства команд пакета plots. При обращении к ней для каждой из перечисленных ниже областей, на которые смешанная система делит двумерную плоскость, возможно задание собственных значений опций после указания опции, идентифицитующей соответствующую область:

• область, удовлетворяющая системе неравенств optionsfeasible=(опции));
• область, не удовлетворяющая хотя бы одному неравенству из заданной смешанной системы (optionsexcluded=(опции));
• область границы строгих неравенств (optionsopen=(опции));
• область границы нестрогих неравенств и равенств (optionsclosed=(опции)).

После задания соответствующей опции области в правой части в круглых скобках задаются обычные графические опции, имеющие значение для указаной области, например, цвет области, цвет и толщина линии границы.

Отображение решения смешанной системы неравенств и равенств:
	Пример иллюстрирует общее использование команды построения решения смешанной системы на плоскости.

Замечание: На рисунке область красного цвета соответствует области решения неравенств, сиреневого - области, не удовлетворяющей системе неравенств. Черная линия представляет область границы строгих неравенств, а толстая зеленая линия - область границы нестрогих неравенств и равенств, входящих в смешаную систему.

Отображение многоугольников:
	Команда polygonplot() строит на плоскости один или несколько мноугольников, заданных своими вершинами. Каждый многоугольник задается в виде списка координат его вершин, представленных в форме двуэлементных списков. В случае отображения нескольких многоугольников они задаются либо списком, либо множеством.

Функция плотности и линии уровня поверхностей:

Две двумерные графические команды отбражают на плоскости значения функции двух независимых переменных: densityplot() - в виде функции плотности линий уровня (более темные области соответствуют большим значениям функции и наоборот - более светлые представляют меньшие значения функции) и contourplot() - в виде линий уровня. При отображении функции плотности линий уровня по умолчанию отбражаются линии сетки, на которой она рассчитывается. Установкой значений опции style, равной patchnogrid, можно отменить отображение линий сетки.

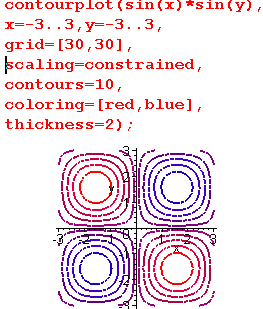
Команда contourplot() по умолчанию отображает восемь линий уровня. Изменить это значение можно опцией contours, значением которой является количество линий уровня или список значений линий уровней.Опцией coloring задается цвет линии уровня с наименьшим значением. Все остальные отбражаются цветом соответствующего оттенка между указанными цветами в двуэлементном списке.

Если значение опции filled установлено равным true, то отбражается функция плотности линий уровня с указанным цветовым переходом и линии уровня черным цветом.

Отображение поля градиентов функции и векторного поля на плоскости:

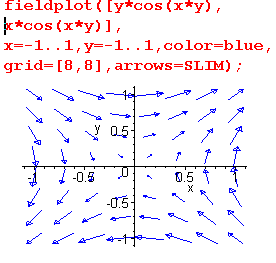
Команды gradplot() и fieldlplot() похожи в том отношении, что обе они отображают векторные поля на плоскости. Обе эти команды для задания размеров и вида отображаемых векторов используют опцию arrows, которая может принимать следующие значения: THIN (умалчиваемое значение), LINE, SLIM или THICK. Опцией color задается функция двух переменных, которая используется для определения цвета вектора в точке. Векторное поле для команды fieldplot() задается в виде двуэлементного списка координат векторов, представленных функциями двух независимых переменных.

Отображение поля градиентов заданной функции двух переменных.	Отображение простого векторного поля, определяемое координатами векторов в заданных точках поля.

 

Решение дифференциальных уравнений:
	Команда odeplot() используется для отображения численного решения задачи Коши для дифференциального уравнения или системы дифференциальных уравнений. Ее первым параметром является построенная командой dsolve() с опцией type=numeric процедура численнго решения задачи Коши, а вторым списковым параметром задаются отображаемые по горизонтальной и вертикальной осям виличины.
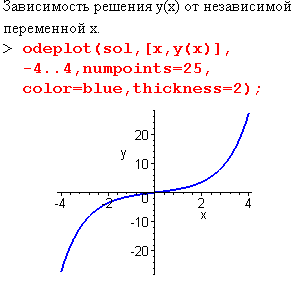
	Например, чтобы отбразить искомую функцию решения y(x), следует задать список [x,y(x)].
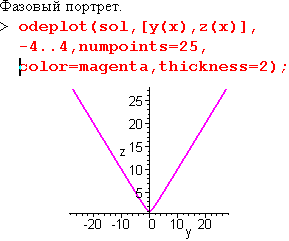
	Если элементами списка являются неизвестные функции системы дифференциальных уравнений, то будет построен фазовый портрет решения задачи Коши. Можно отбразить на одном графике несколько зависимостей, определяя их в виде списка.

Последняя команда двумерного графического отбражения, которую мы опишем, - команда textplot() отображения текста в заданной точке графика. Она отбражает так называемые текстовые точки, которые определяются трехэлементным списком. Первые два элемента этого списка являются координатами точки привязки текста на плоскости, а третий элемент - строка выводимого текста.

Опцией align можно указать расположение текста относительно точки привязки: ABOVE - выше, BELOW - ниже, RIGHT - правее и LEFT - левее. Если необходимо задать несколько значений этой опции, то их задают в виде множества. Для отбражения нескольких надписей следует задать список текстовых точек в качестве первого параметра функции textplot().

Замечание: Для совмещения на одном рисунке выводов нескольких графических команд использована команда display(), описание которой будет дано ниже в этой главе.

 

Предыдущая9101112131415161718192021222324Следующая

Поделиться:

Воспользуйтесь поиском по сайту: