 |
Средства отладки процедур, их сохранение и использование (подключение)
|
|
|
|
Одним из основных средств отладки процедур является функция трассировки trace(имя процедуры). Детальность ее работы задается системной переменной printlevel:=n (уравень вывода). При n=1 результат выводится только для непосредственно исполняемой функции или оператора. Для вывода информации о выполнении k-го уровня вложеннсти надо использовать знечения этой переменной от 5*k до 5*(k+1). Так, при n от 1 дл 5 выводятся результаты трассировки первого уровня, при n от 6 до 10 - второго и т.д. Максимальное значение n=100 обеспечивает трассировку по всем уровням вложенности процедуры.
Для отладки процедур в системе Maple имеется специальный интерактивный отладчик - debugger. Для включения отладчика в работу необходимо подать команду:
Stopat(имя процедуры)
Признаком, указывающим на работу отладчика, является изменение приглашения к вводу со знака > на DBG>. Теперь, подавая команды next (следующий), step (шаг) и stop (остановка), можно проследить выполнение процедуры.
С помощью команды showstat (имя процедуры) можно вывести ее листинг, причем в нем строки вычисляемых элеменотов пронумерованы, что весьма удобно при разборе работы процедуры.
Существует множество других команд отладчика. Справку по ним можно получить выполнив команду ?Debugging
Когда процедура отлажена и оттестирована, ее можно сохранить в файле с расширением m командой save(), которая позволяет сохранить любой объект Maple.

Впоследствии, когда для вычислений потребуется данная процедура, ее можно прочитать в другом сеансе Maple командой read().
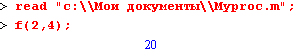
Решение алгебраических уравнений и систем уравнений
Основная функция solve. Одиночные нелинейные и тригонометрические уравнения. Системы нелинейных и трансцендентных уравнений
|
|
|
Основная функция solve
Для решения линейных и нелинейных уравнений в аналитическом виде используется достаточно универсальная и гибкая функция
solve(eqn, var)
solve({eqn1, eqn2,...}, {var1, var2,...})
где eqn-уравнение, содержащее функцию ряда переменных, var-переменная, по которой ищется решение. Если решение содержит повторяющиеся выражения, Maple V обозначает их как %1, %2 и т.д. и выводит решение с такими переменными.
Характер решений можно изменить с помощью глобальных переменных:
_SolutionsMayBeLost - при значении true дает решение при возврате функцией solve значения NULL;
_MaxSols - задает максимальное число решений;
_EnvAllSolutions - при значении true задает выдачу всех решений.
В решениях помимо переменных %N могут встречаться следующие обозначения:
_NN - указывает на неотрицательные решения;
_B - указывает на решения в бинарной форме;
_Z - указывает на то, что решение содержит целые числа.
Одиночные нелинейные и тригонометрические уравнения
Решение одиночных нелинейных уравнений вида f(x)=0 легко обеспечивается функцией solve(f(x),x). Например:
> solve(x^3-2*x+1,x);
1/2 1/2
1,1/25 -1/2,-1/2-1/25
> solve(x^(3/2)=3,x);
2/3
3
Функция solve старается дать решение в аналитическом виде. Для получения корней в численном виде надо использовать функцию evalf или convert.
> s:=solve(sqrt(ln(x))=2,x);
> s1:=evalf(s);
> convert(s,float);
s:= exp(4)
s1:= 54.59815003
54.59815003
Часто бывает удобно представлять уравнение и его решения в виде отдельных объектов, отождествленных с определенной переменной.Это позволяет в дальнейшем использовать полученные решения в других вычислениях. В частности, это позволяет легко проверить решение подстановкой subs:
> e1:={x^3-2*x+1=0};
> s:=solve(e1,x);
3
e1:= {x - 2 x + 1 = 0}
s:= {x = 1}, {x = -1/2 + 1/2 sqrt(5)},
{x = -1/2 - 1/2 sqrt(5)}
> subs(s[2],e1);evalf(%);
3
{(-1/2 + 1/2 sqrt(5)) + 2 - sqrt(5) = 0}
{0 = 0}
Если результат решения представлен через функцию RootOf, то получить все корни можно через функцию allvalues.
|
|
|
> solve({exp(x)=sin(x)},x);
{x = RootOf(_Z - ln(sin(_Z)))}
> allvalues(%);
{x =.3627020561 - 1.133745919 I}
> a:=solve({x^5-2*x=-3},x);
5
a:= {x = RootOf(_Z - 2 _Z + 3)}
> allvalues(a);
{x = -1.423605849},
{x = -.2467292569 - 1.320816347 I},
{x = -.2467292569 + 1.320816347 I},
{x =.9585321812 -.4984277790 I},
{x =.9585321812 +.4984277790 I}
Сводящиеся к одному уравнения вида f1(x)=f2(x) также решаются функцией solve(f1(x)=f2(x),x).
При решении тригонометрических уравнений периодичность тригонометрических функций и связанная с этим множественность решений не учитывается.
> solve(sin(x)=cos(x)-1, x);
- 1/2 Pi, 0
В данном примере найдено одно главное решение. Используя системную переменную _EnvAllSolutions, которой присвавается значение true (по умолчанию - false), можно получить все решения.
> _EnvAllSolutions:= true:
> solve(sin(x)=cos(x)-1, x);
- 1/2 Pi + 2 Pi _Z~, 2 Pi _Z~
В данном примере переменные _Z~ означают ряд натуральных чисел. Таким образом, получены все решения уравнения с учетом периодичности тригонометрических функций.
|
|
|


