 |
Основные геометрические параметры эвольвентного зуба.
|
|
|
|
Выберем на одной прямой (прямой зацепления) центры основных окружностей – точки О1 и О2 (Рис. IX. 5). Обкатывание основной окружности по общей касательной дает эвольвенты ведущего и ведомого колес. Точка пересечения прямой зацепления и касательной, называемая полюсом зацепления W, делит межосевое (межцентровое) расстояние а ω на части, обратно пропорциональные угловым скоростям ω1 и ω 2:
.
Рис. IX. 5
Нормаль ТТ к межцентровому расстоянию дает угол αω. В соответствии с ГОСТом этот угол равен 20º. Соприкасающиеся друг с другом окружности на ведущем и ведомом колесах, обкатывающиеся друг по другу без скольжения, называются начальными и обозначаются dω1 и dω2. Диаметр начальной окружности связан с диаметром основной окружности соотношением:
.
Расстояние между одноименными сторонами двух соседних зубьев колеса, измеренное по дуге начальной окружности, называется шагом зацепления Рt. Шаг Ро расположения зубьев по основной окружности является проекцией шага зацепления по начальной окружности на линию зацепления:
.
Делительной окружностью зуб делится на головку ha зуба и ножку hf,сам зуб ограничивается окружностью впадин диаметра df и окружностью выступов диаметра dа (Рис. IX. 6).
Рис. IX. 6
Высота h зуба складывается из высоты ножки зуба и высоты головки зуба:
.
Как правило, начальная и делительная окружности совпадают.
Теоретически эвольвентные зубья при взаимном обкатывании не дают проскальзывания и трения, что является главным достоинством эвольвентного зацепления. Пара колес с эвольвентным зацеплением дает высокий КПД (около 0,99) при передачи крутящего момента, т.е. потери на трение сравнительно малы.
|
|
|
Для нормального зацепления двух колес необходимо учитывать некоторые особенности взаимодействия зубчатых колес:
1. Линия зацепления (общая касательная) всегда нормальна к касательной к эвольвенте, причем при взаимном обкатывании точки касания зубьев находятся на линии зацеплении.
2. Шаг расположения зубьев у шестерни и колеса должен быть одинаковым:
,
где z 1 и z 2 – число зубьев шестерни и колеса соответственно.
Величина 
является постоянной для данного колеса (зацепления) и называется модулем зацепления m. Тогда:
.
Модуль зацепления m представляет собой универсальную величину, через которую определяются все геометрические параметры эвольвентного зацепления. Для определенности, согласно ГОСТу высота головки зуба принимается равной модулю:
,
высота ножки зуба берется большей, что связано с опасностью заклинивания, т.е. ответный зуб не должен касаться впадины другого зуба:
.
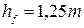Высота зуба равна:
,
диаметр окружности выступов:
,
диаметр окружности впадин:
.
Выбор модуля зацепления значительно влияет на геометрию зацепления, а значит, и на прочность и виброустойчивость пары зубчатого зацепления. Возьмем окружность диаметра dа и точку пересечения ее с линией зацепления, тогда контакт пары зубьев будет происходить по линии А1А2 (Рис. IX. 7), т.е. зубья встречаются в точке А1, а расходятся в точке А2. Часть А1А2 линии зацепления называется активной зоной линии зацепления.
Рис. IX. 7
Следовательно, длина активной линии зацепления должна быть не менее шага зацепления:
. (IX. 1)
Величина ε называется коэффициентом перекрытия. По нормативам 
, что говорит о том, что в данный момент в контакте находятся больше 1 пары зубьев. При малом ε будет происходить ударное взаимодействие зубьев, что влечет за собой отсутствие непрерывного плавного зацепления, а также усиленные вибрации при передачи крутящего момента.
|
|
|
Из формулы (IX. 1) следует, что с увеличением модуля m уменьшается коэффициент перекрытия ε. Следовательно необходимо выбирать такой модуль зацепления, чтобы обеспечивался плавный ход зацепления.
Контактные напряжения.
Взаимодействие ответного зуба в точке K контакта передает комплекс усилий (Рис. IX. 8).
Рис. IX. 8
Радиальное R и крутящее Т усилия дают полное усилие F, действующее от одного зуба на другой:
.
Для прямозубых колес наиболее опасно действие крутящего усилия Т при плече h, т.е. изгибающего момента Мх, ведущего к возникновению нормального напряжения σ:
,
где Wx – осевой момент сопротивления сечения зуба.
Теоретически принято:
,
значит:
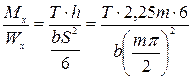. (IX. 2)
Выражение (IX. 2) показывает, что при увеличении модуля зацепления (или увеличении толщины S зуба) уменьшается напряжение.
Расчет зуба на изгиб является основным элементом расчета на прочность зубчатых зацеплений открытого типа. В случае закрытых передач опасным является не напряжение изгиба, а напряжение контактного типа, возникающее в зоне контакта профилей зубьев. Поэтому расчет на прочность колес закрытых передач производится через определенную величину межосного расстояния аω, рассчитываемого по полуэмпирической формуле:
,
где u – передаточное отношение, равное:
,
[ σк ] – допускаемое контактное напряжение для пары колес;
ψав – коэффициент пропорциональности, изменяющийся в пределах 0,1…0,2;
Кн – коэффициент динамического режима работы пары колес.
Косозубые передачи.
Косозубые передачи (Рис. IX. 9) обладают некоторыми преимуществами перед прямозубыми – это безударность работы, плавность хода и, следовательно, независимость коэффициента перекрытия от особенностей проектирования.
Рис. IX. 9
Расчет косозубых передач ведется по нормальному модулю m:
,
где Рt – дуговой шаг расположения зубьев, определенный по нормали к профилю зуба:
,
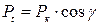где Рк – шаг расположения косозубого колеса.
Модуль косозубого зацепления mк равен:
.
|
|
|
