 |
Расчет детали на скручивание.
|
|
|
|
Рассмотрим модель горизонтальной жестко заделанной балки и мысленно выделим из нее элементарный участок (Рис. V.4).
Рис. V.4
Если γ – угол поворота балки – постоянный, то со временем меняется и угол поворота сечения dφ, тогда длина дуги bb ' равна:
,
где ρ – расстояние от оси балки до элементарной площадки сечения (Рис. V.5, а).
А) б)
Рис. V.5
Тогда:
.
При использовании формулы (V.1), получим:
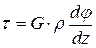. (V.2)
Из закона распределения касательных напряжений следует, что крутящий момент dМz в сечении представляет собой равнодействующий момент касательных напряжений в сечении:
,
где dA – площадь элементарной площадки.
Тогда полный внутренний крутящий момент Мz:
или:
.
Из курса теоретической механики известно:
,
где Iρ - полярный момент инерции сечения.
Тогда используя формулу (V.2), получим формулу распределения касательного напряжения по сечению:
.
Значение касательного напряжения определяется величиной радиуса ρ от оси балки до элементарной площадки сечения (Рис. V. 6):
Рис. V. 6
если ρ =0, то τ =0
если ρ =max= d /2, то τ =max.
Внутренняя зона (ρ ~0) не сопротивляется скручиванию, поэтому валы обычно делают с осевым отверстием, т.е. валы кольцевого сечения.
Оценка деформации вала заключается в определении угла поворота φ вала под действием крутящего момента:
,
тогда:
.
Произведение Iρ · G является механической характеристикой материала и называется жесткостью.
Iρ – геометрическая характеристика сечения, которая показывает закономерность распределения элементарных площадок по всему сечению, при этом описывает способность сечения сопротивляться скручиванию. Размерность полярного момента инерции сечения:
|
|
|
.
Размерность полярного момента выводится из расчета статистического момента сечения,
определяемым интегралом:
,
тогда:
,
для балки прямоугольного сечения основной геометрической характеристикой при расчете на прочность является осевой момент инерции сечения Ix (Рис. V. 5, б):
.
Если радиус ρ разложить по теореме Пифагора:
,
то полярный момент инерции сечения равен:
,
тогда для круглого сечения:
.
Часто вместо полярного момента инерции сечения используется полярный момент сопротивления Wρ:
.
VI. Изгиб.
Изгиб – деформация тела балки под действием сил в продольных плоскостях. Изгиб бывает поперечный (происходит под действием сил и моментов), чистый (действует только изгибающий момент) или плоский (ось балки прогибается в одной плоскости).
Рассмотрим случай чистого изгиба (Рис. VI.1) – балка изогнута под действием изгибающих моментов.
Рис. VI. 1
Исходя из характера деформации балки можно установить, что при чистом изгибе происходит поворот поперечных сечений без искажения, тогда как продольные слои балки деформируются (сжимаются и растягиваются) (Рис. VI. 2).
Рис. VI. 2
ρ – радиус кривизны слоя;
θ – угол поворота торца.
Как видно из рис. VI. 2 на выпуклой стороне слои балки растягиваются, что приводит к появлению положительного напряжения (+ σ), а на вогнутой – сжимаются (- σ), с возникновением отрицательного напряжения (+ σ). В средней зоне, т.е. на оси балки, нет напряжений и нет деформаций – это нейтральный слой (нейтральная ось), длина которого не меняется.
С целью вывода формул для определения нормального напряжения и кривизны балки рассмотрим элементарный участок длиной l (Рис. VI. 3).
Рис. VI. 3
Исходная длина балки – ОО1, dθ – угол поворота торцевых перемещений, у – расстояние от нейтральной оси до некоторого слоя.
|
|
|
Если из точки О провести линию, параллельную правому торцу, дуга bc будет равна ОО1, а дуга аb – абсолютному удлинению торцов изгиба, т.е.:
,
тогда относительная деформация равна:
или
,
тогда:
. (VI. 1)
Введем величину k, называемую собственной кривизной и равную:
. (VI. 2)
Из аналитической геометрии следует:
. (VI. 3)
Степень в знаменателе формулы (VI. 3) существенно не влияет на равенство в связи с тем, что деформации жесткой балки малы, т.е. ими можно пренебречь, тогда:
.
Применяя закон Гука:
и формулы (VI. 1) и (VI. 2), получим формулу для определения нормального напряжения в любом слое балки (Рис. VI. 4):
.
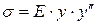Рис. VI. 4
Напряжение σ и его плечо у образует момент, тогда для элементарной площадки можно вывести формулу внутреннего изгибающего момента dMx:
,
полный внутренний изгибающий момент Mx равен:
или
,
где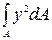 
- осевой момент инерции сечения Ix,
тогда:
,
следовательно:
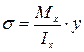. (VI. 4)
Формула (VI. 4) позволяет вести расчет на прочность сечения изогнутой балки. Но на практике обычно вместо осевого момента инерции сечения Ix используют осевой момент сопротивления сечения Wx, равный:
.
Физический смысл Ix сводится к тому, что эта величина – геометрическая характеристика сечения, описывающая закономерность распределения элементарных площадок по всему сечению, а так же показывающая способность сечения сопротивляться изгибу. Таким образом, условием статической прочности балки при изгибе является выражение:
.
В зависимости от расстояния между элементарной площадкой сечения и осью балки изменяется напряжение при изгибе (Рис. VI. 5): чем дальше элементарная площадка от оси, тем больше величина напряжения (формула (VI. 4)).
Рис. VI. 5
В связи с этим рациональным является использование именно балки прямоугольного сечения, называемые двутаврами, средний слой которой не сопротивляется изгибу (Рис. V. 6).
Рис. VI. 6
|
|
|
