 |
XII. Надежность деталей машин.
|
|
|
|
Устойчивость стержней.
Устойчивость – способность детали сохранять исходную геометрическую форму. Стержнем называют удлиненную деталь.
Наиболее опасным нагружением для стержня является продольный изгиб – изгиб под действием осевой продольной силы F (Рис. XII. 1).
Рис. XII. 1
До достижения некоторой величины Fкрит сила F сжимает стержень. При ослаблении нагрузки стержень вернется к исходной геометрической форме. С последующим увеличением силы наблюдается изгиб стержня, при этом остаточные деформации не позволяют вернуться к первоначальной форме.
Изгиб стержня осуществляется в сторону минимального момента Imin инерции сечения стержня, т.е. каждое из его поперечных сечений поворачивается вокруг той оси, относительно которой момент инерции минимален (Рис. XII. 2, а):
а) б)
Рис. XII. 2
,
,
,
следовательно:
.
Тогда, используя уравнение изогнутой балки:
,
можно описать изгиб стержня (Рис. XII. 2, б):
, (XII. 1)
где у – плечо действия силы F.
Обозначим:
,
тогда из уравнения (XII. 1) получим дифференциальное уравнение второго порядка:
общее решение которого:
. (XII. 2)
Наложение граничащих условий позволяет определить величины А и В уравнения (XII. 2). Если z = 0, тогда y = 0 и sin (kz) = 0, следовательно В = 0. Значит:
. (XII. 3)
Аналогично, при z, равном l, частным решением дифференциального уравнения (XII. 2) является уравнение (XII. 3). Однако, синус – функция периодическая, т.е.:
,
где n = 0, 1, 2, 3, …
При n > 1 стержень изгибается по кривой, включающей n полуволн (Рис. XII. 3).
Рис. XII. 3
Однако, практический анализ показывает, что эти решения не представляют интереса, т.к. описывают неработоспособные состояния вала (стержня). Наибольший интерес представляет решение:
|
|
|
. (XII. 4)
Исходя из уравнения (XII. 4) получим:
,
тогда критическое значение сжимающей силы Fкр для рассчитываемого стержня определяется по формуле:
. (XII. 5)
Рис. XII. 4
На практике величина прогиба у зависит от способа заделки стержня, для чего в формулу (XII. 5) вводится приведенная длина стержня lприв:
,
где μ – коэффициент приведения длины (Рис. XII. 4),
тогда:
.
Величина критического напряжения σкр исходя из формулы (XII. 5):
.
Отношение Imin / A называется радиусом инерции I, тогда:
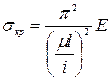, (XII. 6)
где соотношение μl / I является гибкостью λ стержня,
,
тогда формулу (XII. 6) можно переписать:
. (XII. 7)
Выражение (XII. 7) называется формулой Эйлера.
Для стержней из малоуглеродистой стали формула Эйлера справедлива при гибкостях λ > 100, а также при λ > 80 – для чугуна. Обобщение этих данных сводится к построению диаграммы (Рис. XII. 5), связывающей критическое напряжение σкр с гибкостью λ вала (или стержня).
Рис. XII. 5
Стержни, для которых справедлива формула Эйлера, называются особо гибкими (зона III). Для стальных стержней с гибкостью λ < 100 формула Эйлера несправедлива. Для расчета таких стержней используется полученная в результате обработки опытных данных формула Ясинского:
,
где а и b – величины, характеризующие качество материала, значения которых приводятся в технических справочниках. Для стали средней гибкости (зона II) формула Ясинского приводится к виду:
.
Для стержней, у которых критическое напряжение превышает предел текучести (гибкие стержни), критическое напряжение σкр приравнивают пределу текучести σ т (зона I), т.е. зона I диаграммы определяет состояние текучести материала, потерявшего свою работоспособность. Отсюда следует, что жесткие стержни при продольном нагружении следует рассчитывать на прочность. Гибкие валы рассчитываются на устойчивость, затем в случае необходимости – на прочность. Сам расчет на прочность ведется по предельному напряжению устойчивости [ σу ]:
|
|
|
,
где [ nу ] – коэффициент запаса устойчивости продольно нагруженного стержня.
Как правило:
,
где [ σ ] – предел прочности вала;
φ – величина, зависящая от гибкости λ вала (стержня) (Табл. XII. 1).
| λ | |||||
| φ | 0,9 | 0,8 | 0,65 | 0,3 |
Табл. XII. 1
Практическое значение этих расчетов заключается в определении компоновки машины, например, шнекового транспортера (Рис. XII. 6).
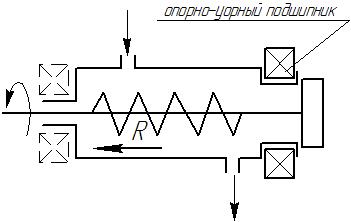
Рис. XII. 6
Основной задачей при конструировании машины является определение положения упорного подшипника. В случае, если подшипник поставить в начале вала, то под действием реактивной силы R вал при вращении будет сжиматься, что может привести к изгибу вала. Если шнек изогнется, то коснется корпуса транспортера. Поэтому рациональнее опорно-упорный подшипник размещать в конце трассы перемещения, тогда вал подвергается растяжению, а не изгибу.
|
|
|
