 |
X. Теория взаимозаменяемости.
|
|
|
|
Часто в производстве приходится менять детали машины, что требует массового изготовления деталей. Теория взаимозаменяемости получила свое распространение в результате необходимости массового изготовления одинаковых деталей. При этом взаимозаменяемость базируется на простых постулатах:
1. Невозможно изготовить абсолютно одинаковые детали.
2. Чем точнее деталь изготавливается, тем она дороже.
3. Зачастую дешевле заменить изношенную деталь машины, чем приобретать новую машину.
Допуски и посадки.
Все детали машин, рассматриваемые механикой, делятся на отверстия и валы. Отверстие – элемент (или деталь), охватывающий ответную деталь. Вал - элемент (или деталь), охватываемый отверстием. Размер (номинальный) посадочного места для отверстия обозначается заглавной латинской буквой (А, В, С и т.д.), для вала – латинской прописной (а, b, с и т.д.) (Рис. X.1).

Рис. X. 1
В связи с тем, что никогда точно нельзя деталь изготовить (причиной чего может быть неточность изготовления инструментов, оборудования самого изготовления детали и др.), вводят максимальный, минимальный номинальный размеры. Номинальный размер элемента детали получают из расчетов или принимают из конструктивных соображений. Максимальный и минимальный размеры являются наибольшим и наименьшим предельными размерами детали соответственно.
На практике допускается отклонение реального размера от номинального в определенных пределах, т.е. вал (или отверстие) может быть изготовлен с некоторыми отклонениями (Рис. X. 2).
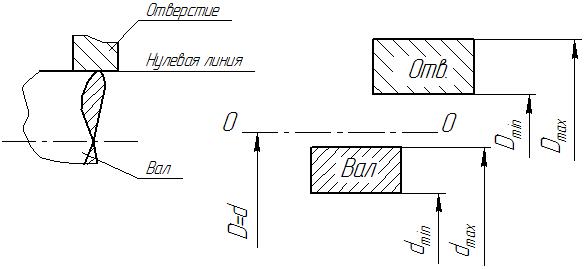
Рис. X. 2
Верхним предельным отклонением размера называется разница между наибольшим предельным и номинальным размерами для вала:

и для отверстия:
|
|
|
 .
.
Нижним предельным отклонением размера называется разница между наименьшим предельным и номинальным размерами для вала:

и для отверстия:
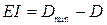 .
.
Величина допускаемого отклонения Т – разница между максимальным и минимальным размерами для отверстия:
 ,
,
для вала:
 .
.
Диапазон допускаемых размеров называется полем допуска. Допуски определяют характер изготовления и сопряжения деталей. Разработаны стандарты (порядка 28 разновидностей) расположения полей допусков и их обозначений.

Рис. Х. 3
Для полей Н (для отверстия) и h (для вала) нижнее предельное отклонение EI и верхнее предельное отклонение es соответственно равны нулю (Рис. X. 3). Поля a, b, c, d, …, g показывают, что вал меньше номинального, поля от А до H – больше номинала, а начиная с поля H и ниже отверстия становятся уже.
Точность изготовления детали определяется квалитетом точности (всего 19 квалитетов). Графически квалитет показывает высоту поля допуска. Чем меньше квалитет, тем более жесткие требования предъявляются к изготовлению детали. Самые точные детали изготавливаются с квалитетами 0, 01, 1, 2, 3, 4, что составляют первую группу квалитетов, используемую в точной механике и ответственных отраслях промышленности. Вторая группа (5, 6, …, 10) используется для изготовления обычного, наиболее распространенного оборудования. Квалитеты точности для несопрягаемых поверхностей составляют третью группу.
На чертежах величины верхнего и нижнего предельных отклонений указываются в скобках мелкими цифрами (мм) за номинальным размером и полем допуска, например,  или
или  .
.
Примечание. Нулевые значения предельных отклонений размеров на чертежах не пишутся!
Определенное назначение поля допуска определяет посадку в данном сопряжении. В соответствие с ГОСТом посадки делят на посадки с зазором, с натягом и переходные посадки, допускающие наличие как зазора, так и натяга.
|
|
|
Зазором называется пространство (щель) между валом и отверстием (Рис. Х. 4). Максимальным зазором является разница между наибольшим размером отверстия и наименьшим размером вала:
 ,
,
следовательно, допуском на назначаемый зазор является сумма величин допусков для отверстия и вала:
 .
.
Особенностью посадки с зазором является то, что на схеме сопряжения поле допуска отверстия располагается всегда выше поля допуска вала, расположение нулевой линии может быть любым.

Рис. Х. 4
Посадка с натягом обеспечивает неподвижное соединение деталей, поля допуска отверстия и вала позволяют оценить степень неподвижности. Имея в виду то, что при посадки с натягом вал должен быть больше отверстия, мы можем определить величину натяга (Рис. Х. 5).

Рис. Х. 5
Максимальный натяг Nmax:

и минимальный натяг Nmin:
 ,
,
тогда допуск размера натяга TN:
 .
.
Особенностью посадок с гарантированным натягом является то, что поле допуска вала всегда располагается под полем допуска отверстия, тогда как расположение нулевой линии может быть любым.
Некоторые особенности имеют и переходные посадки (Рис. Х. 6).

Рис. Х. 6
Максимальным зазором для данной посадки является:
 ,
,
минимальный зазор (показано пунктиром) равен нулю. В переходных посадках поля допуска отверстия и вала могут либо пересекаться, либо включать себя друг в друга.
Особенность обеспечения посадок зависит от того, каким образом изготавливаются вал и отверстие. В этом плане различают системы изготовления или обеспечения посадок – систему отверстия и систему вала, которые отличаются тем, что технологически отверстие изготавливать труднее, чем наружную поверхность вала. Легче купить стандартное изделие – вал или отверстие, а дальше подгонять отверстие или вал соответственно под него.
Система отверстия, где все отверстия изготавливаются с полем допуска Н, наиболее предпочтительна. Поле Н характеризуется тем, что нижнее предельное отклонение равно нулю, т.е. поле лежит на нулевой линии, при этом требуемая посадка обеспечивается подбором поля допуска вала Td (Рис. Х. 7).

Рис. Х. 7
В системе вала все валы изготавливаются с полем h, при котором верхнее предельное отклонение равно нулю, а требуемая посадка обеспечивается подбором поля допуска отверстия (Рис. Х. 8).
|
|
|

Рис. Х. 8
Признаком того, что данное сопряжение выполнено в той или иной системе, является обозначение полей. Например, посадка  выполнена в системе отверстия, т.к. поле допуска отверстия в данной посадке – Н; посадка
выполнена в системе отверстия, т.к. поле допуска отверстия в данной посадке – Н; посадка  – в системе вала (поле допуска вала – h).
– в системе вала (поле допуска вала – h).
Примером посадки в системе отверстия является посадка подшипника качения на вал редуктора (Рис. Х. 9).

Рис. Х. 9
На хвостовик вала насаживается подшипник с небольшим натягом в системе отверстия. При посадки подшипника в корпус работает система вала (подшипник является стандартным изделием). Посадка подшипника на вал и в корпус должна обеспечивать отсутствие значительных зазоров.
ХI. Опоры валов.
Опора вала – базовый элемент расположения всех вращающихся деталей машины. По своему назначению подшипники подразделяются на опорные, воспринимающие радиальную нагрузку R (Рис. XI. 1, а), осевые, обеспечивающие осевую реакцию Q (Рис. ХI. 1, б), и опорно-упорные (или радиально-осевые), обеспечивающие реакции как радиальные R, так и осевые Q (Рис. ХI. 1, в).

а) б) в)
Рис. ХI. 1
По принципу действия опоры делятся на подшипники качения и подшипники скольжения.
Подшипники скольжения.
Опора, выполненная в виде подшипника и работающая, преодолевая трение скольжения, называется подшипником скольжения. Подшипник скольжения является парой вращения, состоящей из опорного участка вала (цапфы) 1 и собственно подшипника 2, в котором скользит цапфа (Рис. ХI. 2, а).

А) б)
Рис. ХI. 2
Цапфу, передающую радиальную нагрузку, называют шипом при расположении ее в конце вала (Рис. ХI. 2, а), и шейкой, если она находится в середине вала (Рис. ХI. 2, б). Форма рабочей поверхности подшипников и цапф может быть цилиндрической, конической или шаровой (применяется редко). Для уменьшения силы трения в подшипнике используется вкладыш 3 (Рис. ХI. 3), изготавливаемый из материала с малым коэффициентом трения (Бронза БрАЖХ, баббит (сплав свинца и олова), пирографит и углефторопласт, используемые в космической технике для обеспечения работы в вакууме).
|
|
|

Рис. ХI. 3
Подшипник в зазоре С должен иметь слой масла (Рис. ХI. 4). Однако если вал не вращается, то он лежит на вкладыше, а масло – неподвижным слоем в зазоре. При вращении вала масло «затаскивается» в зазор между валом и вкладышем, при этом вал всплывает в масляном слое. Такое взаимодействие приводит к тому, что в зоне, где вал опирается на вкладыш, развивается зона повышенного давления в слое масла. Так как непосредственный контакт отсутствует, то трение в подшипнике определяется законами гидродинамики.

Рис. XI. 4
Суть расчета сводится к определению величины подъема h вала (Рис. XI. 4), определяемой соотношением высот неровностей шероховатостей Rz вала и отверстия:
 ,
,
где ∆h – некоторая добавка.
За гидравлическим расчетом подшипников скольжения, как правило, следует проверка, осуществляемая в два этапа:
1 – расчет на прочность (износостойкость), суть которого сводится к тому, что удельное давление p вала на опорной поверхности подшипника не должно превышать допускаемой величины [ p ]:
 ,
,
где F – радиальная сила, с которой вал воздействует на опору;
l – длина опорной поверхности;
d – диаметр цапфы.
2 – тепловой расчет, базируемый на применении комплекса:
 ,
,
где р – давление, организуемое валом на опорной поверхности;
v – линейная окружная скорость на периферии цапфы. Анализ размерностей комплекса рv:

 ,
,
тогда:

В итоге величина рv – энергия, затрачиваемая в единичном времени на энергию преодоления трения, переходящую в тепловую энергию. В связи с этим масло нагревается, а значит:
 ,
,
где Gм – расход масла;
См – теплоемкость масла;
∆t – температурный градиент, величина нагрева масла.
Тогда расход масла Gм:
 .
.
Эти режимные параметры позволяют выбрать необходимый режим работы подшипника с учетом того, что трение f (или коэффициент трения) изменяется с изменением угловой скорости ω вращения вала (Рис. ХI. 5).

Рис. XI. 5
Режим сухого трения (зона I) характеризуется малыми ω, при этом цапфа и вкладыш подшипника находятся в непосредственном контакте – коэффициент трения f принимает наибольшее значение. Увеличение ω приводит к увеличению масляного слоя между контактирующими поверхностями (зона II), в связи с чем наблюдается резкое уменьшение трения f – режим полужидкостного трения. Начиная с некоторой угловой скорости ω = ωкр, при которой коэффициент трения принимает наименьшее значение f = fmin, вал отходит от подшипника (всплывает). Последующее увеличение угловой скорости (зона III) приводит к увеличению масляного слоя между валом и вкладышем подшипника, что приводит к увеличению трения – режим жидкостного трения.
|
|
|
Достоинствами подшипников скольжения являются бесшумность хода, способность работать с большими мощностями, малые радиальные габариты и простота монтажа (сборки), однако при этом необходимость обильной смазки и использования цветных металлов и сплавов, а также значительные осевые габариты являются недостатком подшипников скольжения. Особенность подшипников скольжения заключается в том, что опора разрушается с предварительными признаками разрушения.
Подшипники качения.
Наиболее часто на практике используются подшипники качения. Опора, работающая, преодолевая силу трения качения, называется подшипником качения. Достоинствами подшипников качения являются малая по сравнению с силой трения скольжения сила трения качения, возможность использования стандартных покупных изделий (т.е. возможность взаимозаменяемости) и малые осевые габариты; недостатки – большие радиальные габариты, некоторая сложность при монтаже и возможность внезапного разрушения.

Рис. XI. 6
Подшипник качения имеет внутреннюю 1 и наружную 2 обоймы, комплект тел качения 3 (Рис. ХI. 6). Во избежание соприкосновения тел качения они отделяются друг от друга сепаратором 4. Некоторые подшипники снабжаются защитными шайбами.
По форме тел качения подшипники подразделяются на шариковые (Рис. ХI. 7) и роликовые (Рис. ХI. 8). Последние, в свою очередь, делят по форме роликов на подшипники с короткими (Рис. ХI. 8, а) и длинными (Рис. ХI. 8, д) цилиндрическими роликами, с коническими (Рис. ХI. 8, г), бочкообразными (Рис. ХI. 8, б) и игольчатыми (Рис. ХI. 8, в) роликами.
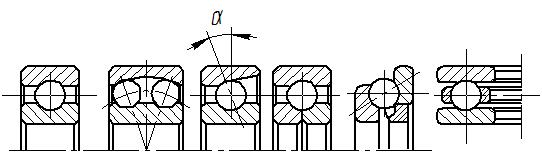
а) б) в) г) д) е)
Рис. XI. 7
По числу рядов тел качения (расположенных по ширине подшипника) подшипники делят на однорядные (Рис. ХI. 7, а, в – е и ХI. 8, а, в – д), двухрядные (Рис. ХI. 7, б и ХI. 8, б) и четырехрядные.

а) б) в) г) д)
Рис. XI. 8
Принцип действия подшипника качения основан на обкатывании тела качения 3 на внутренней обойме 1 вокруг собственной оси и перекатывании его по наружной обойме 2 (Рис. ХI. 9).

Рис. XI. 9
Кинематика работы подшипника несколько усложнена тем, что тело качения совершает плоско-параллельное движение, поэтому подшипник не может быть рассчитан строго теоретически. Надежность и долговечность работы подшипника качения позволяют обеспечить экспериментальные данные и рекомендации. Экспериментально определяется кривая выносливости подшипника качения (Рис. ХI. 10), которая аналогично кривой усталостной прочности показывает функциональную зависимость приведенной радиальной нагрузки RЕ при динамическом нагружении подшипника от долговечности L подшипника:
 ,
,
где m – показатель выносливости, равный 3 для шариковых подшипников и 10/3 – для роликовых (ролик выдерживает большую нагрузку).

Рис. XI. 10
В паспорт (каталог) подшипника выносится динамическая нагрузка (или грузоподъемность) С, которую данный подшипник выдержит при долговечности L =1 млн. оборотов. Следовательно:
 ,
,
тогда любая динамическая нагрузка С рассчитывается по формуле:
 ,
,
где L – долговечность подшипника в млн. оборотов.
В задачах обычно долговечность Lh задается в часах, следовательно:
 ,
,
где:
 .
.
Приведенная нагрузка RE подшипника рассчитывается по формуле:
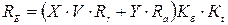 ,
,
где Х, Y – коэффициенты радиальной Rr и осевой Rа нагрузок соответственно;
V – коэффициент вида работы, равный 1 при вращении внутренней обоймы и 1,2 – при вращении наружной обоймы;
Кб – эксплутационный коэффициент нагруженности, определяемый сроком службы;
Кt температурный коэффициент, изменяющийся с увеличением температуры tº подшипникого узла.
Радиальная Rr и осевая Rа нагрузки определяются с учетом добавки осевого усилия S от самого подшипника (Рис. XI. 11), зависящим от угла γ конусности данного подшипника.

Рис. XI. 11
По вычисленной приведенной нагрузке RЕ определяют требуемую динамическую грузоподъемность Стр:

и исходя из условия:

подбирается подшипник качения.
|
|
|


