 |
2. Теоретические основы метода
|
|
|
|
2. Теоретические основы метода
Методы такого комплексного многомерного анализа были разработаны сравнительно недавно, но их развитие было весьма динамичным, и к настоящему моменту они широко распространены как средство анализа в самых разных отраслях науки.
Теоретической основой метода выступает представление о каждом конкретном объекте как о некой «точке», помещенной во вполне конкретное место многомерного пространства (поля или, если хотите, информационного поля), каждая координатная ось которого соответствует одному из признаков в системе признаков, используемых для анализа. При этом каждая характеристика объекта (каждое проявление каждого из его признаков) рассматривается как соответствующая количественная величина одного из многочисленных (по количеству мерности многомерного пространства) векторов. Иными словами местоположение «точки» в многомерном пространстве определяется многочисленными координатами (по количеству мерности многомерного пространства), выраженными в количественном виде. А расстояние между объектами в таком многомерном пространстве есть обобщенная разница в их координатах. Для наглядности и детализации представления о таком подходе к организации исследований рассмотрим ряд очевидных (понимаемых однозначно) позиций или примеров.
Пространство будем понимать как область распространения точек.
Если точки (сравниваемые объекты) размещены на одной прямой (описаны одним параметром) то имеет место одномерное пространство. Координаты каждой точки в нем имеют одномерное описание, которое соответствует разности между началом координат (0) и координатами, соответствующими конкретному проявлению признака у объекта. В частности в сравнительном анализе деревьев (или насаждений) по одному признаку (по диаметру ствола) значения признаков можно отложить на одной прямой в соответствующем масштабе.
|
|
|
ПРИМЕР.
Диаметр одного ствола равен 20 см: т. е. от условной точки начала координат на линейной оси «0 см» до конкретного значения «20 см» расстояние составляет 20 единиц выбранной шкалы. Диаметр другого ствола 24 см: от точки начала координат на линейной оси «0 см» до конкретного значения «24 см» расстояние составляет 24 единиц выбранной шкалы. Разница между ними составит 4 см (24 см – 20 см). Визуально представляемым примером этих рассуждений может выступать процедура измерения диаметра стволов на высоте 1. 3 м (или ствола на разной высоте) с помощью мерной вилки. Неподвижная рейка фиксирует «нулевое» значение координат. Отодвигаясь от неё на то или иное расстояние, подвижная рейка каждый раз фиксирует значение диаметра, соответствующее координате точки отсчета значения.
Текущее задание
2. Приведите собственные примеры одномерных количественных характеристик (параметров) объектов из сферы Ваших научных интересов: агрономия, биология, агрохимия, механика, экономика, лесное хозяйство, зоотехния, ветеринария и др.
Графическое отображение наших рассуждений можно представить в следующем виде:

Если попытаться наши рассуждения перевести в язык математических алгоритмов, то получим несложную формулу, представленную ниже. Её можно конкретизировать, подставляя вместо буквенных символов конкретные численные выражения.

Один признак – одномерное пространство (прямая линия); два признака – двухмерное пространство (площадь, например, шахматная доска); три признака – трехмерное пространство (объем, например, кубик Рубика); четыре и более признаков – более сложное пространство. Попробуем графически изобразить это на рисунке (рис. 1).
|
|
|
Добавить формулы для 2-мерного и 3-мерного пространства!!!!
  |
 Y1
Y1
 |
 X1
X1
|
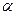
Схема
 |




 | |||
 | |||
|
|
|


