Статистическое расстояние между природными (реальными)

Статистическое расстояние между природными (реальными)

и эталонной (гипотетической) популяциями облепихи

 

№ п. п.	Популяции в поймах рек и в прибрежных зонах озер	Обобщенное статистическое расстояние
		по статистическому расстоянию в евклидовом пространстве		по обобщенному расстоянию Махаланобиса
		величина расстояния	ранговая оценка	величина расстояния	Ранговая оценка
1.	Бес-Агач	9, 061		80, 765
2.	Каркара	6, 829		38, 917
3.	Каинды	7, 995		59, 582
4.	Чилик	7, 194		49, 676
5.	Кульсай	7, 660		56, 920
6.	Большая Алма-Атинка	6, 420		36, 246
7.	Чу	9, 149		81, 268
8.	Усек	5, 841		33, 707
9.	Каратал	6, 291		38, 768
10.	Лепсы	6, 239		37, 573
11.	Аксай	6, 282		37, 646
12.	Бель-Булак	7, 346		49, 713
13.	Баян-Кол	7, 118		45, 391
14.	Тасты-Булак	7, 271		48, 967
15.	Зайсан	1, 587		2, 767

 

Используя критерий «норма» можно разделить весь комплекс сравниваемых объектов на три категории: «лучшие», «нормальные», «худшие». Критерий «норма» устанавливается в соответствии с величиной среднего квадратического отклонения обобщенного статистического расстояния. К «нормальным» относят объекты, имеющие величины обобщенного статистического расстояния, отклоняющиеся от средней величины обобщенного статистического расстояния на величину, равную 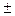2/3 σ. В эту категорию будут отнесены все объекты, которые имеют величину обобщенного статистического расстояния от эталонного объекта в пределах 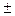2/3 σ от средней величины такого расстояния. К категории «лучших» будут относиться объекты, чьё статистическое расстояние до эталонного объекта меньше, чем минимальное значение границ «нормальности», т. е. меньше, чем средняя величина обобщенного статистического расстояния минус 2/3 σ. К категории «худших» будут относиться объекты, чьё обобщенное статистическое расстояние до эталонного объекта будет больше, чем величина максимальной границы «нормальности», т. е. больше, чем среднее значение обобщенного статистического расстояния плюс 2/3 σ.

 

Для вычисления критерия «норма» полученные значения обобщенных статистических расстояний между реальными объектами и эталонным объектом рассматривают как вариационный ряд и рассчитывают для него среднюю величину и среднее квадратическое отклонение. Затем по формуле: М 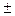2/3 σ вычисляют границы «нормальности»: верхнюю – по формуле М+2/3 σ; нижнюю – по формуле М-2/3 σ.

 

*************

Одним из перспективных направлений развития применения данного метода является возможность использования его для определения доли участия каждого отдельного признака в формировании обобщенного статистического расстояния между объектами. Иными словами, удается определить ту часть обобщенных различий (часть обобщенного расстояния) между объектами, которая образуется (формируется) под влиянием конкретного признака (фактора). Определяется отрезок – участок- обобщенного вектора в многомерном пространстве, определяющего обобщенное статистическое расстояние между объектами в этом многомерном пространстве.

Фактически дается оценка силы влияния фактора (в данном случае признака) на формирование статистических различий между объектами при их комплексной сравнительной оценке. Оценивается тот отрезок обобщенного статистического расстояния между объектами, который формируется под влиянием отдельного фактора.

, где

 

diy_(j) – обобщенное статистическое расстояние между двумя сравниваемыми объектами по одному признаку;

i = 1, 2, 3, …n – индекс порядкового номера одного из двух сравниваемых объектов;

y = 1, 2, 3, …n – индекс порядкового номера другого из двух сравниваемых объектов;

k – количество анализируемых признаков, введенных в комплекс сравнения;

j = 1, 2, 3, … k – индекс порядкового номера признака, по которому ведется расчет доли обобщенного статистического расстояния.

 

Для сравнения можно рассмотреть формулу обобщенного статистического расстояния по всему комплексу признаков.

diy = (b_i1-b_y1)²+(b_i2-b_y2)²+(b_i3-b_y3)²+…+(b_ik-b_yk)² ,

 

Получив такую оценку доли участия каждого отдельного признака в формировании обобщенного статистического расстояния между объектами, исследователь может дать оценку степени влияния этого признака, которое он оказывает на дивергенцию популяций – на расхождение объектов под влиянием всего комплекса признаков.

 

Удается определить: какой из признаков является наиболее влиятельным при каждом конкретном случае парного сравнения двух объектов (для каждой пары сравниваемых объектов отдельно). Исследованиями установлено (Бессчетнов, 1994), что различия между объектами (например, популяциями облепихи), оцениваемые по величине обобщенного статистического расстояния, обусловлены неодинаковым по силе влиянием анализируемых факторов. Одни из них оказывают большое влияние, в то время как другие – незначительное. Установлено также (Бессчетнов, 1994), что различия между объектами (популяциями) в разных вариантах их парного сравнения в неодинаковой степени определяются различиями по тому или иному признаку. В одном случае определяющим будет один признак, в другом случае – другой, в третьем случае признаки могут иметь примерно равное значение. Метод позволяет дать объективную количественную оценку силе влияния признака на различия между объектами, выраженную как часть обобщенного статистического расстояния между ними. При этом получаемая оценка будет специфичной для каждой конкретной пары сравниваемых по данному признаку объектов.

 

*****************

ВНИМАНИЕ!

Привести фактические примеры расчетов!

**************

 

**********************

При осуществлении расчетов целесообразно представить каждый из анализируемых объектов как вектор средних. Он состоит из одного ряда чисел, каждое из которых соответствует средней величине конкретного признака, включенного в комплекс сравнения. По сути дела мы получим в этом случае матрицу-строку, характеризующую один из объектов по всему набору признаков. Таких матриц-строк будет столько, сколько объектов участвует в анализе. Все матрицы-строки, характеризующие сравниваемые объекты должны быть одной и той же структуры, т. е. должны иметь одинаковое число строк и одинаковое число столбцов (одинаковое число элементов в строке).

Как следует из формулы расчета обобщенного расстояния Махаланобиса, при сравнении двух объектов (метод предусматривает только парное сравнение) необходимо вычислить разницу (разность) между двумя объектами по каждому из анализируемых признаков. Для этого последовательно производят вычитание значения каждого из признаков «первого» объекта из соответствующих значений признаков «второго» объекта. Иными словами мы находим разность между двумя матрицами-строками в соответствии с правилами вычитания матриц. В результате получаем матрицу значений разностей соответствующих признаков двух объектов, которая по своей структуре также является матрицей-строкой (также, как и сравниваемые векторы средних двух объектов являются матрицами-строками) и имеет такую же структуру, как и матрицы-строки, содержащие средние величины сравниваемых объектов. При сравнении некоторого количества (комплекса) объектов таких матриц-строк, содержащих разности средних сравниваемых объектов, будет столько, сколько вариантов сравнения было принято в анализе. Так при сопоставлении каждого многомерного объекта с каждым в комплексе, состоящем из 10 объектов, таких сопоставлений, (матриц-строк) будет 100. При этом 10 из них будут являться вариантами сравнения объекта с самим собой и, следовательно, будут представлены нулевыми значениями, а оставшиеся 90 вариантов сопоставления будут представлены двумя группами по 45, в каждой из которых каждый объект сопоставляется с оставшимися другими в прямом и обратном сочетании соответственно.

На следующем этапе вычислений необходимо выполнить умножение матрицы-строки, содержащей разности между матрицами-строками средних сравниваемых объектов, на матрицу, обратную по отношению к обобщенной ковариационой матрице. Обратная ковариационная матрица по своей структуре квадратная, симметричная и имеет столько строк и столбцов, сколько элементов (что соответствует количеству столбцов) в матрице-строке разности средних. Это число равно числу сравниваемых признаков. Оно является количеством столбцов (элементов) в матрице-строке разности средних и количеством строк и столбцов в обратной ковариационной матрице. Следовательно, вычисление произведения этих матриц в указанном порядке возможно, что следует из правил операций матричной алгебры. Результатом умножения матрицы-строки на симметричную матрицу соответствующей размерности явится матрица-строка, структура и размерность которой соответствуют структуре и строке матрицы, являющейся первым сомножителем. Таких матриц-строк произведений будет столько, сколько вариантов сопоставления по два возможно в принятом комплексе сравниваемых объектов – столько же, сколько матриц-строк разности средних возможно в этом комплексе сравнения.

Далее, как следует из формулы расчета обобщенного расстояния Махаланобиса, требуется умножить полученную матрицу произведений (она является матрицей-строкой) на транспонированную матрицу разности средних (её транспонирование даст матрицу-столбец). При транспонировании матриц первый столбец исходной матрицы становится первой строкой новой матрицы, второй столбец – второй строкой и т. д. При этом очередность элементов в строке транспонированной матрицы соответствует очередности элементов соответствующего столбца исходной матрицы. Умножение указанных матриц возможно, поскольку число столбцов в матрице, стоящей первым сомножителем (равно числу анализируемых признаков) равно числу строк в матрице, стоящей вторым сомножителем (равно числу анализируемых признаков). В результате умножения этих матриц (матрицы-строки на матрицу-столбец) образуется одно единственное число (матрица, состоящая из одного числа), равное расстоянию Махаланобиса между двумя сравниваемыми многомерными объектами. Это вытекает из правила умножения матриц – матрица-произведение имеет столько строк, сколько их у первого сомножителя (1), и столько столбцов, сколько их у второго сомножителя (1). Понятно, что таких значений расстояния Махаланобиса будет вычислено столько, сколько вариантов сопоставления будет принято в многомерном анализе. При полном сопоставлении каждого объекта комплекса с каждым образуется квадратная симметричная матрица значений. На её главной диагонали стоят нулевые значения расстояний Махаланобиса, что соответствуем тому, что объект не удален от самого себя. Верхняя и нижняя треугольные части симметричны. В них располагаются значения расстояний Махаланобиса между не одноименными объектами. Они всегда положительны. При этом прямое расстояние между двумя объектами равно обратному расстоянию между ними. Последнее обстоятельство и обусловливает симметричность полученной матрицы значений.

 

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: