 |
4. Техника применения метода
|
|
|
|
Используемая в качестве исходного материала матрица средних значений (табл. 1) представлена размерными и безразмерными неравнозначными величинами, характеризующими объект (популяцию, экотип, плюсовые деревья на ЛСП и т. п. ), например длина листовой пластинки – в сантиметрах, масса плода (или шишки) – в граммах или миллиграммах, площадь листовой пластинки – в сантиметрах квадратных, коэффициент формы плода (или шишки) – в безразмерных величинах.
ПРИМЕР.
Примером такой матрицы исходных размерных и неоднородных значений может служить таблица средних значений признаков у различных популяций облепихи крушиновидной (табл. 1, представлена ниже).
Особенностью метода является возможность использования в расчетах статистических комплексов, представленных только однородными величинами, что наиболее удобно представлять в форме безразмерных величин.
(Использовать же в расчетах возможно только однородные безразмерные величины. )
Для этой цели матрица исходных данных преобразуется в матрицу нормированных значений (табл. 2).
ПРИМЕЧАНИЕ.
К вопросу о «НОРМИРОВАНИИ»: (см. Меркурьева, 1970, стр. 66, «Нормированное отклонение»).
При этом все они являются безразмерными, их распределение обеспечивает нулевое среднее значение (среднее значение всех нормированных величин в пределах каждого признака в сумме даст «ноль»), а среднеквадратическое отклонение равно единице (учитывается среднеквадратическое отклонение каждого из средних, введенных в комплекс сравнения, от обобщенного среднего).
ПРИМЕР.
Примером матрицы нормированных значений может явиться таблица нормированных значений признаков популяций облепихи (табл. 2). Эта таблица представлена ниже.
|
|
|
Нормирование производится путем следующего преобразования каждого исходного значения, включенного в исходную матрицу:
1. Разница между каждым исходным значением признака и его обобщенным средним значением делится на обобщенное среднеквадратическое отклонение. Здесь каждое исходное значение признака – это среднее его значение для популяции (или экотипа и т. п. ), полученное в результате статистической обработки исходного фактического материала, полученного на объекте (в популяции, в пределах сорта или экотипа и т. д. ) в ходе биометрирования учетных растений, составляющих выборку. Обобщенное среднее значение получается в результате математической обработки всего обобщенного цифрового массива, представляющего совокупность всех частных (в пределах популяции, сорта, экотипа и т. п. ) выборок. Обобщенное среднеквадратическое отклонение высчитывается в ходе статистической обработки обобщенной выборки (обобщенного цифрового массива, включающего в себя все частные выборки по популяциям или экотипам). Следовательно, обобщенный статистический анализ дает две статистики (две величины), используемые для нормирования: обобщенное среднее значение по каждому признаку и обобщенное среднеквадратическое отклонение по каждому признаку.
ПРИМЕЧАНИЕ
Принципиально, нормирование и приведение данных (дат) к сопоставимому безразмерному виду возможно с применением достаточно многочисленного набора алгоритмов. В качестве примера они приведены ниже (Лейтас и др., 1983, стр. 29, 30).
По максимальному значению признака в совокупности:
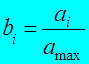 ,
,
По среднему значению признака в совокупности:
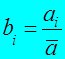

По минимальному значению признака в совокупности:
 ,
,
По значению десятичного логарифма:
 ,
,
По среднеквадратическому отклонению:
|
|
|
 ,
,
По значению квадратного корня:
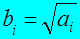 ,
,
По значению арксинуса:
 ,
,
По значению минимальной разности и диапазону значений:
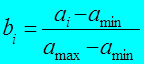 ,
,
По значению средней разности и диапазону значений:
 ,
,
По значению среднего квадратного:
 .
.
В представленной выше ситуации логичнее было бы привести ещё один способ нормирования, а именно по максимальной разнице:
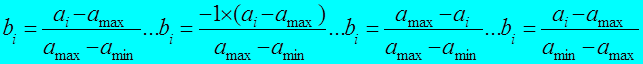
Понятно, что достичь положительного значения результатов такого нормирования можно путем умножения всего выражения на «- 1» или посредством перестановок в числителе или знаменателе. Принципиально, это не требуется, поскольку квадрат разности любых чисел, как следует из ниже приведенной формулы, всегда положителен, тем более что речь идет о соотносительных расстояниях между объектами только данного комплекса.
Таблица 1.
|
|
|


