 |
Основные понятия, термины и определения
|
|
|
|
ВЕКТОР (от латинского слова vector – несущий), отрезок прямой определенной длины и направления.
Следовательно, каждый вектор имеет такие параметры как:
- величина (длина собственно вектора – собственно длина данного отрезка прямой);
- координаты начальной и конечной точек (координаты точек в любом выбранном многомерном пространстве, соответствующие длине отрезка на соответствующей координатной оси от точки начала координат до точки пересечения с координатной осью перпендикуляров, опущенных из начальной и конечной точек на векторе);
- направление, которое определяется ориентацией вектора по отношению к известным направлениям координатных осей и задается соответствующими углами наклона линии вектора к каждой линии осей координат.
Два вектора будут равны лишь в том случае, когда совпадают и их длина, и их направление.
С изменением ориентации вектора изменяется и его знак: знак вектора может измениться с «+» на «-», если его направление изменилось на противоположное в пределах одной прямой линии.
Вектор, как правило, обозначают малой прописной буквой жирного шрифта, соответствующей букве начальной точки вектора, например, вектор а или он же вектор АВ. Абсолютная величина вектора (его длина) записывается так: | a| либо АВ (первая буква начало вектора, а вторая буква конец вектора).
Вектором, как правило, изображают так называемые векторные величины, показатель измерения которых имеет некоторую направленность: силу, скорость, ускорение и т. п. Они по определению имеют такую характеристику как направление.
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ вектора а на вектор b есть вектор р, количественно равный по длине площади параллелограмма, построенного на векторах а и b, и перпендикулярный плоскости этого параллелограмма и направленный так, что тройка векторов будет правой или левой в зависимости от порядка сомножителей.
|
|
|
 | |||
 | |||
p = [ a, b ]
b
j
р
a
 |
b p = [ b, a ]
jjj
p
a
Рисунок 1. 3 – Векторное произведение [ a, b ] = - [ b, a ], т. е. векторное произведение зависит от порядка сомножителей
ВЕКТОРНОЕ ПРОСТРАНСТВО – это математическое понятие, обобщающее понятие совокупности всех свободных векторов 3-х мерного (в общем случае многомерного пространства на случай произвольного числа наблюдений).
ЕВКЛИДОВО ПРОСТРАНСТВО – это пространство, свойства которого изучаются в евклидовой геометрии. В более широком понимании евклидовым пространством называют n-мерное векторное пространство, в котором определено скалярное произведение.
Евклидово пространство (в математике) – это пространство, свойства которого описываются аксиомами евклидовой геометрии.
В более общем смысле евклидовым пространством называется n-мepное векторное пространство, в котором возможно ввести некоторые специальные координаты (декартовы) так, что метрика его будет определена следующим образом: если точка М имеет координаты (х1, х2,..., xn), а точка М* — координаты (x1*, x2*,..., xn*), то расстояние между этими точками будет:
|
|
|
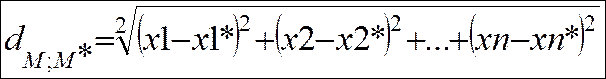
Многомерное пространство – это пространство, имеющее число измерений (размерность) более трёх. Обычное евклидово пространство, изучаемое в элементарной геометрии, трёхмерно; плоскости — двумерны, прямые — одномерны.
Вместе с тем, как мы только что отметили выше, принципы вычисления значений расстояния между двумя точками в многомерном пространстве останутся неизменными и при 2-мерном пространстве, и – при 1-мерном.
Возникновение понятия «многомерное пространство» (М. п. ) связано с процессом обобщения самого предмета геометрии. В основе этого процесса лежит открытие отношений и форм, сходных с пространственными, для многочисленных классов математических объектов (зачастую не имеющих геометрического характера). В ходе этого процесса постепенно выкристаллизовалась идея абстрактного математического пространства как системы элементов любой природы, между которыми установлены отношения, сходные с теми или иными важными отношениями между точками обычного пространства. Наиболее общее выражение эта идея нашла в таких понятиях, как топологическое пространство и, в частности, метрическое пространство. Простейшими метрическими пространствами являются n-мерные евклидовы пространства, где n может быть любым натуральным числом.
Вместе с тем в теории математики рассматривают «0-мерное пространство». Принципиально, мерность пространства может быть определена не только натуральными числами, но и более сложными их представлениями, включая рациональные или даже иррациональные числа.
Подобно тому, как положение точки обычного евклидова пространства определяется заданием трёх её прямоугольных координат, «точка» n-мерного евклидова пространства задаётся n «координатами» x1, x2, ..., xn (которые могут принимать любые действительные значения); расстояние r между двумя точками M(x1, x2, ..., xn) и М'(у1, y2, ..., yn) определяется формулой аналогичной формуле расстояния между двумя точками обычного евклидова пространства. С сохранением такой же аналогии обобщаются на случай n-мерного пространства и другие геометрические понятия. Так, в многомерном пространстве рассматриваются не только двумерные плоскости, но и k-мерные плоскости (k < n), которые, как и в обычном евклидовом пространстве, определяются линейными уравнениями (или системами таких уравнений). Понятие n-мерного евклидова пространства имеет важные применения в теории функций многих переменных, позволяя трактовать функцию n переменных как функцию точки этого пространства и тем самым применять геометрические представления и методы к изучению функций любого числа переменных (а не только одного, двух или трёх). Это и было главным стимулом к оформлению понятия n-мерного евклидова пространства.
|
|
|
Важную роль играют и другие М. п. Так, при изложении физического принципа относительности пользуются четырёхмерным пространством, элементами которого являются т. н. «мировые точки». При этом в понятии «мировой точки» (в отличие от точки обычного пространства) объединяется определённое положение в пространстве с определённым положением во времени (поэтому «мировые точки» и задаются четырьмя координатами вместо трёх). Квадратом «расстояния» между «мировыми точками» М’(х’, y’, z’, t’) и М’’(х’’, y’’, z’’, t’’), где первые три «координаты» — пространственные, а четвёртая — временная, принято считать выражение: (M’ M’’)2 = (x’ - x’’)2 + (y’ — y’’)2 + (z’ — z’’)2 — c2(t’ — t’’)2, где с — скорость света. Отрицательность последнего члена делает это пространство «псевдоевклидовым». Вообще n-мерным пространством называется топологическое пространство, которое в каждой своей точке имеет размерность n. В наиболее важных случаях это означает, что каждая точка обладает окрестностью, гомеоморфной открытому шару n-мерного евклидова пространства.
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ векторов – это произведение векторов а и b, образующее число (скаляр), равное произведению длин этих векторов на косинус угла j между ними.
Скалярное произведение обозначается как ( а, b ), тогда формулу скалярного произведения можно изобразить как ( а, b ) = | a | ´ | b | ´ cosj. При этом следует учитывать, что векторы имеют одну общую точку, и имеет место соотношение:
|
|
|
а
j
 |
b
Рисунок 1. 4. – Скалярное произведение векторов.
СКАЛЯР (от латинского scalaris – ступенчатый), величина, каждое значение которой (в отличие от вектора) может быть выражено одним действительным числом, вследствие чего совокупность значений скаляра можно изобразить на линейной шкале (от слова scala - скала: отсюда и название величины – скаляр). Примерами скалярных величин могут выступать длина, площадь, время, температура и др. СКАЛЯР часто называют скалярной величиной.
КОВАРИАЦИЯ. В математической статистике ковариация – это средняя из произведений отклонений двух переменных Х и Y от их средних (соответственно) значений (Моисейченко, Заверюха, Трифонова, 1994, стр. 353):
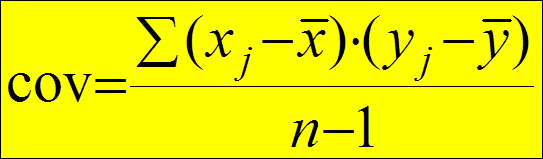, где
- текущее значение переменной «Х»;
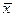- среднее значение переменной «Х»;
- текущее значение переменной «У»;
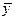- среднее значение переменной «У»;
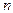- число пар текущих значений двух сравниваемых признаков в ковариационном
комплексе.
Ковариационная оценка применяется, когда необходимо установить соотношение (или взаимосвязь) между варьированием двух показателей, находящихся во взаимозависимости друг от друга, которая однозначно не определена как корреляционная или функциональная и является неопределенной. Ковариационный анализ применяют для приведения фактических средних по ряду одного признака (Х – длина плодоножки) к полной выравненности условий по ряду другого признака (У – масса плода). В случае применения многофакторного анализа ковариационная оценка позволяет (и необходима) перейти от независимых значений одного признака ко взаимоуравненным значениям между признаками – к значениям (безразмерным) признака с учетом его взаимодействия с другими. Построение матрицы ковариационных оценок (ковариационной матрицы) позволяет перейти от оценок комплекса независимых неоднородных и разноразмерных признаков к операциям с одноразмерными (безразмерными на основе использования значений ковариации) признаками, построенным на основе учета взаимовлияния признаков во всех возможных вариантах (или условиях) их взаимодействия.
Ковариационный анализ часто рассматривают как метод, объединяющий возможности регрессионного, корреляционного и дисперсионного анализов.
|
|
|
НОРМИРОВАНОЕ ОТКЛОНЕНИЕ. Это важный статистический показатель, позволяющий определять изменчивость признаков. С его помощью можно выразить в относительных единицах (долях σ ) отклонение каждого конкретного члена совокупности (х) от средней арифметической (М).
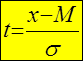, где
t – нормированное отклонение;
σ – среднеквадратическое отклонение или стандартное отклонение;
х – текущее (частное) значение признака;
М – среднее значение признака в анализируемой совокупности.
При нормированном отклонении можно сравнить члены разных совокупностей по одноименному признаку, предполагается, что изменчивость признака в разных совокупностях может быть неодинаковой.
Необходимость введения в расчеты нормированного отклонения вызвана необходимостью работы с разными (в том числе и по характеру изменчивости одноименных признаков) совокупностями.
ПРИМЕР.
Даже один и тот же параметр можно выразить разными по величине и обозначению единицами измерения. Например, меру длины или расстояние можно выразить в метрах, сантиметрах, футах (англ. «нога или стопа»), вершках, дюймах, саженях, световых годах или иных единицах измерения. Логически их сопоставление затруднено или невозможно. Эта проблема наглядно рассматривается в одном из детских мульт-сериалов, персонажами которого выступают Слоненок, Обезьянка, Удав, Попугай и Мартышка. В одной из серий они пытались измерять длину удава в попугаях, мартышках и других эталонах (единицах) измерений. При этом каждый раз у них возникали различные количественные оценки одного и того же параметра – длины удава. Перевод величин в нормированную форму снимает указанную проблему.
|
|
|
