 |
μab = 1/(1+ dab).. N(N-1) i<j f=1
|
|
|
|
μ ab = 1/(1+ dab).
Существуют достаточно адекватные статистики для измерения расстояния между объектами в пространстве m признаков. Некоторые из них приведены ниже.
1. Линейное расстояние:
dLij = Σ │ xil – xjl │ = Σ │ xi – xj │ l =
l=1, m
xil – нормированное значение l-го признака у i-го объекта;
xjl – нормированное значение l-го признака у j-го объекта;
l = 1, m – индекс признака, принимает значение 1, 2, 3, …m;
i = 1, n – индекс одного из сравниваемых объектов, принимает значение 1, 2, 3, … n;
j = 1, n – индекс второго из сравниваемых объектов, принимает значение 1, 2, 3, … n;
m – количество признаков, определяющее мерность пространства;
n – количество объектов сравниваемых между собой в многомерном пространстве признаков;
Линейное расстояние является метрикой (мерой расстояния между многомерными объектами), заслуживающей большего внимания, чем ему уделяется в настоящее время. По своему смысловому содержанию оно очень близко евклидову расстоянию и призвано учесть величину обобщенного удаления (по всем признакам) одного многомерного объекта от другого. По сути дела, различия между линейным расстоянием и евклидовым расстоянием состоят только в математическом механизме преодоления проблемы нахождения сумм значений разности между многомерными объектами по многочисленным признакам в ситуации, когда часть значений может оказаться (по вполне понятным причинам) отрицательной, а часть значений – положительной, и их сумма может оказаться равной нулю, при том, что объекты не идентичны. В евклидовом расстоянии математический механизм представляет собой возведение каждого значения разности в квадрат, что обеспечивает положительность значения, а в дальнейшем из суммы квадратов разностей извлекают квадратный корень, для того чтобы компенсировать увеличение различий, возникающее при возведении в степень. В линейном расстоянии математический механизм состоит в использовании абсолютных значений разности между объектам по каждому из анализируемых признаков и в последующем их суммировании для получения интегральной величины обобщенного расстояния. В кластерном анализе применяется в ситуациях, когда заранее известно, что кластеры имеют плоскую форму, то есть все их объекты расположены на некоторой одной плоскости. По вполне понятным причинам реализация этого алгоритма предусматривает предварительное нормирование, в противном случае процедура суммирования оказывается нелогичной (невозможно суммировать штуки с килограммами и сантиметрами…).
|
|
|
2. Евклидово расстояние:
dEij = ﴾ Σ ﴾ xil – xjl ﴿ 2﴿ 1/2 = ﴾ Σ ﴾ xi – xj﴿ l2﴿ 1/2
l=1, m
xil – значение l-го признака у i-го объекта;
xjl – значение l-го признака у j-го объекта;
l = 1, m – индекс обозначения признака, принимает значение 1, 2, 3, …m;
i = 1, n – индекс одного из сравниваемых объектов, принимает значение 1 … n;
j = 1, n – индекс второго из сравниваемых объектов, принимает значение 1 … n;
m – количество признаков, определяющее мерность пространства;
n – количество объектов сравниваемых между собой в многомерном пространстве признаков;
Выбор метода потенциальных функций для решения задачи кластеризации основан на квадрате евклидова расстояния между группируемыми объектами (матричная запись):
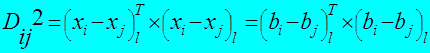, где:
xi – вектор-столбец значений всех признаков от 1 до m на i-м объекте;
xj – вектор-столбец значений всех признаков от 1 до m на j-м объекте.
bi – вектор нормированных значений всех признаков от 1 до m на i-м объекте;
bj – вектор нормированных значений всех признаков от 1 до m на j-м объекте.
|
|
|
l =1, m – индекс обозначения признака, принимает значение 1, 2, 3, …m;
Само евклидово расстояние вычисляется по формуле (матричная запись):
.
Евклидово расстояние является наиболее удобной и часто употребляемой метрикой в кластерном анализе. Оно соответствует интуитивным представлениям близости, а, кроме того, в силу своей квадратичной формы удачно вписывается в традиционные статистические конструкции. Необходимым условием его реализации является переход от натуральных значений признаков к их нормированным значениям. Геометрически оно наилучшим образом объединяет объекты в шарообразных скоплениях, которые весьма типичны для слабо коррелированных совокупностей. Евклидово расстояние часто употребляется для кластеров шаровидной формы (не плоских). По вполне понятным причинам реализация и этого алгоритма предусматривает необходимость предварительного нормирования показателей, в противном случае процедура суммирования оказывается нелогичной (невозможно суммировать штуки с килограммами и сантиметрами…).
3. Расстояние Махаланобиса:
dMij = ﴾ xi – xj ﴿ l T × Wij- 1 × ﴾ xi – xj ﴿ l
l=1, m (применена матричная запись)
xil – значение l-го признака у i-го объекта;
xjl – значение l-го признака у j-го объекта;
l =1, m – индекс признака, принимает значение 1, 2, 3, …m;
i = 1, n – индекс одного из сравниваемых объектов, принимает значение 1, 2, 3, … n;
j = 1, n – индекс второго из сравниваемых объектов, принимает значение 1, 2, 3, … n;
m – количество признаков, определяющее мерность пространства;
n – количество объектов в многомерном пространстве;
xi – вектор-столбец значений всех признаков от 1 до m на i-м объекте;
xj – вектор-столбец значений всех признаков от 1 до m на j-м объекте.
W-1 – матрица обратная обобщенной ковариационной матрице для данной пары объектов.
Расстояние Махаланобиса представляет собой весьма своеобразную статистическую конструкцию. Одной из его особенностей является наличие в формуле расчета матрицы обратной по отношению к обобщенной ковариационной матрице. Наличие в формуле матрицы ковариаций делает расстояние между двумя объектами по какому-либо признаку или группе признаков, зависимым от расстояния по другим признакам. По этой причине наличие аномальных наблюдений может исказить всю матрицу расстояний, что вообще свойственно для дисперсионных статистик.
|
|
|
Кроме того, в ряде случаев обобщенное расстояние Махаланобиса может иметь ограничения в применении для определения степени отдаленности объектов в многомерном пространстве. В частности при росте корреляции между признаками, образующими многомерное пространство, нормировочный эффект, способный нивелировать разницу в дисперсиях, не исчезает, а приобретает достаточно усложненные формы. Так, в ситуации, если корреляция оценивается коэффициентами, значения которых близки к единичным (что нередко возникает при анализе параметров ствола или других параметров дерева или насаждения), а дисперсии почти равны друг другу (что характерно для линейных признаков деревьев и для многих характеристик ствола и кроны или же таксационных показателей насаждений), определитель ковариационной матрицы приближается к нулю. Это означает, что ковариационная матрица становится близкой к вырожденной (такой для которой невозможно получить обратную матрицу), а матрица обратная ковариационной приобретает крайне неустойчивый вид. Такая ситуация способствует произвольному упорядочению расстояний Махаланобиса (они могут приобретать нетипично большие значения, принимать отрицательные значения), что в конечном итоге не позволяет дать корректную оценку взаимного расположения многомерных объектов в пространстве признаков.
Инвариантная статистика Махаланобиса (как и ряд других подобных статистик) имеет весьма полезное свойство – она не меняется при допустимых преобразованиях шкал (шкал измерения расстояний). Вместе с тем она имеет существенное ограничение – статистика Махаланобиса теряет содержательный смысл без предварительного нормирования (Мандель, 1988, стр. 146). Отсюда необходимым условием реализации метода является предварительное нормирование всех переменных – исходных значений признаков. Ковариация, лежащая в их основе, оправдана лишь для заранее соизмеримых (по дисперсиям и величинам) признаков.
|
|
|
Набор расстояний одного объекта до всех остальных объектов в комплексе сравнения называют профилем данного объекта.
Весьма важным условием такой организации кластерного анализа, которая способна привести к корректным и адекватным оценкам реального взаиморасположения многомерных объектов в пространстве признаков, является правильный выбор меры близости между многомерными объектами и правильное построение многомерного пространства. Признаки пространства должны быть строго и однозначно фиксированы, что позволит получить единое и единственное пространство анализа.
Если из содержательных соображений анализа не вытекает предподчительность той или иной шкалы измерения какого-либо (каждого) признака или каждого из всех признаков, то следует переходить к нормированным данным. При этом следует учитывать качественную специфику признаков и тщательно выбирать способ нормировки, и если имеется возможность, то нормирование следует производить только по величинам, не зависящим от выборки.
После формирования пространства признаков следует выбрать меру близости объектов. При этом следует учитывать формальные свойства мер близости (кратко мы их рассмотрели выше). Полезно сделать расчеты несколько раз с разными метриками и найти устойчивые общие черты в разбиении совокупности многомерных объектов на кластеры.
При выборе метрик следует учитывать ряд обстоятельств.
1. Инвариантная статистика Махаланобиса (как и ряд других подобных статистик) имеет весьма полезное свойство – она не меняется при допустимых преобразованиях шкал (шкал измерения расстояний). Вместе с тем она имеет существенное ограничение – статистика Махаланобиса теряет содержательный смысл без предварительного нормирования (Мандель, 1988, стр. 146). Отсюда необходимым условием реализации метода является предварительное нормирование всех переменных – исходных значений признаков. Ковариация, лежащая в их основе, оправдана лишь для заранее соизмеримых (по дисперсиям и величинам) признаков.
2. Если исследователь находится в ситуации, когда отсутствует априорная (заранее известная точная) информация о целесообразности выбора той или иной метрики, предпочтение следует отдавать применению евклидова расстояния, расчет величины которого производится по нормированным значениям признаков. Кроме того, следует учитывать, что (Мандэль, 1988, стр. 85) квадрат евклидова расстояния тесно связан с дисперсионными критериями.
|
|
|
, где:
2 N m
-------------- Σ d2ij = Σ σ 2f
N(N-1) i< j f=1
Эксперименты показали, что искажения евклидова расстояния (за счет изменения количества признаков или их размерности) не очень сильно влияют на результаты работы процедур кластеризации, таких как иерархические процедуры или К-процедуры, результатом работы которых является построение дендрограмм (Мандэель, 1988, стр. 148).
|
|
|
