Средние значения признаков популяций облепихи (исходная матрица)

Средние значения признаков популяций облепихи (исходная матрица)

 

№ п. п.	Популяции в поймах рек и в прибрежных зонах озер	Длина плодо-ножки, мм	Диаметр плода, мм	Длина плода, мм	Масса плода, г	Длина листа, см	Ширина листа, мм	Коэф-фициент формы плода	Коэф-фициент формы листа	Коэф-фициет площади листа	Коли-чество колючек, шт. /дм
1.	Бес-Агач	4, 278	5, 123	5, 950	0, 082	4, 601	3, 983	1, 175	1, 195	1, 349	2, 555
2.	Каркара	2, 545	6, 996	7, 353	0, 214	5, 026	5, 959	1, 054	0, 873	3, 006	2, 128
3.	Каинды	3, 550	5, 517	6, 291	0, 113	5, 205	4, 672	1, 150	1, 153	2, 437
4.	Чилик	4, 163	5, 914	6, 738	0, 133	5, 340	4, 867	1, 146	1, 120	2, 604	2, 366
5.	Кульсай	4, 287	6, 037	6, 578	0, 145	4, 991	4, 613	1, 090	1, 101	2, 346	3, 162
6.	Большая Алма-Атинка	3, 359	6, 429	6, 634	0, 170	6, 254	6, 284	1, 031	1, 009	3, 958	1, 887
7.	Чу	4, 093	5, 523	5, 777	0, 113	4, 441	4, 573	1, 051	0, 998	2, 048	4, 385
8.	Усек	4, 632	6, 098	7, 056	0, 162	6, 725	5, 078	1, 158	1, 337	3, 432	1, 266
9.	Каратал	4, 638	6, 388	7, 641	0, 189	4, 888	4, 993	1, 199	0, 997	2, 501	1, 892
10.	Лепсы	4, 446	6, 459	7, 325	0, 188	5, 160	5, 332	1, 138	0, 977	2, 788	1, 801
11.	Аксай	4, 251	6, 144	6, 768	0, 181	5, 906	5, 336	1, 109	1, 117	3, 211	2, 443
12.	Бель-Булак	3, 562	5, 691	6, 468	0, 146	5, 568	4, 809	1, 138	1, 161	2, 739	2, 113
13.	Баян-Кол	3, 288	5, 943	6, 581	0, 167	5, 605	4, 927	1, 112	1, 183	2, 757	1, 783
14.	Тасты-Булак	3, 617	5, 757	6, 592	0, 124	5, 538	5, 005	1, 157	1, 146	2, 813	1, 538
15.	Зайсан	5, 425	7, 291	10, 068	0, 359	6, 992	7, 175	1, 408	1, 004	5, 060	1, 844

 

Таблица 2.

Нормированные значения признаков популяций облепихи (матрица нормированных значений)

 

№ п. п.	Популяции в поймах рек и в прибрежных зонах озер	Длина плодо-ножки	Диаметр плода	Длина плода	Масса плода	Длина листа	Ширина листа	Коэф-фициент формы плода	Коэф-фициент формы листа	Коэф-фициет площади листа	Коли-чество колючек
1.	Бес-Агач	0, 310	-1, 235	-1, 006	-1, 310	-0, 980	-1, 186	0, 251	0, 466	-1, 181	0, 255
2.	Каркара	-1, 583	1, 181	0, 456	0, 777	-0, 499	0, 825	-0, 649	-1, 017	0, 147	-0, 053
3.	Каинды	-0, 419	-0, 727	-0, 651	-0, 826	-0, 297	-0, 484	0, 060	0, 273	-0, 507	-0, 151
4.	Чилик	0, 176	-0, 216	-0, 186	-0, 497	-0, 144	-0, 286	0, 033	0, 120	-0, 315	0, 119
5.	Кульсай	0, 310	-0, 057	-0, 353	-0, 323	-0, 538	-0, 545	-0, 384	0, 031	-0, 612	0, 692
6.	Большая Алма-Атинка	-0, 698	0, 448	-0, 295	-0, 084	0, 888	1, 156	-0, 821	-0, 391	1, 238	-0, 226
7.	Чу	0, 099	-0, 720	-1, 186	-0, 828	-1, 160	-0, 586	-0, 675	-0, 442	-0, 953	-1, 573
8.	Усек	0, 686	0, 022	0, 144	0, 045	1, 420	-0, 072	0, 124	1, 117	0, 635	-0, 673
9.	Каратал	0, 692	0, 392	0, 753	0, 374	-0, 656	-0, 158	0, 425	-0, 445	-0, 433	-0, 222
10.	Лепсы	0, 484	0, 487	0, 424	0, 358	-0, 347	0, 187	-0, 028	-0, 538	-0, 104	-0, 288
11.	Аксай	0, 271	0, 081	-0, 155	0, 260	0, 495	0, 191	-0, 245	0, 108	0, 382	0, 177
12.	Бель-Булак	-0, 477	-0, 495	-0, 467	-0, 305	0, 113	-0, 345	-0, 026	0, 308	-0, 160	-0, 063
13.	Баян-Кол	-0, 776	-0, 178	-0, 350	0, 034	0, 155	-0, 225	-0, 223	0, 408	-0, 139	-0, 301
14.	Тасты-Булак	-0, 417	-0, 418	-0, 339	-0, 646	0, 079	-0, 146	0, 113	0, 240	-0, 076	-0, 477
15.	Зайсан	1, 548	1, 561	3, 279	3, 059	1, 643	2, 064	1, 978	-0, 415	2, 504	-0, 257

 

ПРИМЕЧАНИЕ.

При наличии достаточной мощности счетной решающей техники преобразование матрицы исходных значений в матрицу нормированных безразмерных однородных величин целесообразнее производить на этапе первичного преобразования каждого первичного исходного значения в каждое первичное нормированное значение и затем рассчитывать величину среднего значения нормированных исходных величин (среднее значение нормированных дат).

 

2. Для расчета обобщенного среднего значения каждого признака и обобщенного среднеквадратического отклонения по нему формируется обобщенная выборка – обобщенный цифровой массив из результатов замеров признака на всех учетных растениях (учетных площадках и т. п. ) во всех популяциях или экотипах (или сортах, формах и т. п. ). Как правило, такие массивы достаточно велики, что вызывает определенные сложности с их статистической обработкой. В этой ситуации полезно применять счетно-решающую программируемую технику – компьютеры. Для решения задачи создают программы расчета, предусматривающие объединение всех частных выборок в единую и её последующую обработку как единого массива. Не исключена возможность использования пакетов прикладных программ, например «ЭКСЭЛЬ», «СТАТГРАФ», «СТАТИСТИКА» и т. д. Однако, в любом случае первоначально необходимо сформировать массив исходных данных. Обработка ведется по каждому признаку отдельно (в программе организуются циклы, повторяющиеся по каждому признаку).

 

3. Кроме этого предусматривается статистическая обработка данных в пределах каждой популяции (экотипа, сорта и т. д. ) с расчетом популяционных средних (и всех необходимых статистик). Для этого применяются такие же программы статистических расчетов, ориентированные на объем выборки в пределах отдельного объекта в комплексе сравниваемых объектов (популяции, сорта, экотипа и т. п. ).

 

4. Полученные в ходе этих (и на популяционном уровне, и на обобщенном уровне) расчетов данные (популяционные средние, обобщенные средние, обобщенные среднеквадратические отклонения по каждому признаку) используются для получения нормированных безразмерных однородных значений. Для этого применяется формула z-преобразования:

       a_ij - А_j

b_ij = ---------, где

          S_j

 

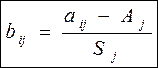, где

 

i = 1, … n – индекс значения (порядковый номер) объекта, (популяции, экотипа или т. п. );

j = 1, …k – индекс значения (порядковый номер) анализируемого признака;

b_ij – элемент матрицы нормированных значений;

a_ij – элемент матрицы исходных значений;

A_j – обобщенное среднее значение j – го признака;

S_j – обобщенное среднеквадратическое отклонение j – го признака;

n – количество сравниваемых объектов в комплексе сравнения (популяций, экотипов, клоновых групп и т. д. );

k – количество анализируемых признаков, введенных в комплекс сравнения.

 

 

Полученная матрица (таблица) преобразованных нормированных значений обладает следующими свойствами:

- каждый столбец (соответствует набору значений нормированных показателей какого-либо признака у разных объектов сравниваемого комплекса объектов – популяций, экотипов, сортов, клонов и т. п. ) имеет нулевое среднее значение, т. е. сумма всех значений нормированного показателя равна «нулю»: М_ср = 0;

- среднеквадратическое отклонение нормированных значений от их средней величины «0» равно «единице»: СКО = 1.

 

Базой сравнения выступает «эталонный объект» (эталонная популяция или эталонный экотип и т. д. ), имеющий наилучшие (наибольшие в смысле размеров плодов, семян, ствола и т. п. или наименьшие в смысле количества колючек на побегах, отпада за единицу времени, поражаемости вредителями и болезнями и т. п. ) показатели. При этом наилучшие показатели могут быть введены только как комплекс наилучших показателей анализируемого комплекса популяций, экотипов сортов и т. п. Здесь следует учитывать то, что «наилучшее значение» признака устанавливается по его реальному ненормированному значению (при сравнении показателей в исходной матрице), но в расчете статистического обобщенного расстояния используются соответствующие ему («лучшему значению») нормированные значения того же признака. В этом случае статистические координаты эталонного объекта можно представить в виде:

 

С = (С₁, С₂, С₃, …, С_К)

 

Тогда расчет обобщенного статистического расстояния между эталонным объектом и каждым конкретным (i - м) реальным объектом (между эталонной популяцией и любой из реальных популяций) может быть представлен в виде:

d_i = (b_i1-c₁)²+(b_i2-c₂)²+(b_i3-c₃)²+…+(b_ik-c_k)², где

 

d_i  - обобщенное статистическое расстояние между i-м объектом и эталонным объектом.

 

Вместе с тем не исключена возможность введения параметров эталонного объекта как комплекса гипотетических параметров, которые должен иметь эталонный объект в соответствии с установленными задачами селекции или другой отрасли лесного хозяйства или лесной науки, даже если они не зафиксированы ни у одного объекта анализируемого комплекса. В этом случае параметры эталонного объекта вводятся в исходную матрицу и учитываются при расчете обобщенного среднего и обобщенного среднеквадратического отклонения. После этого преобразование матрицы исходных значений в матрицу нормированных значений производится по принятой ранее схеме.

 

Ограничением в этом случае может выступать то обстоятельство, что при расчетах обобщенного среднего и обобщенного среднеквадратического отклонения (используемых при нормировании материалов исходной матрицы) трудно учесть статистическое влияние гипотетических параметров гипотетического объекта на обобщенное среднее и обобщенное среднеквадратическое отклонение. Одним из путей преодоления этого ограничения может явиться такая схема расчета, при которой обобщенные статистики рассчитываются на основе статистической обработки материалов исходной матрицы средних, с условием введения в неё параметров гипотетического объекта.

 

ПРИМЕЧАНИЕ.

Преодоление данного (см. предыдущий абзац) ограничения возможно при введении параметров эталонного объекта по всем признакам комплексной оценки в исходную системную матрицу в форме одного из элементов (одного из объектов) по каждому признаку, в форме вариационного ряда, состоящего только из значений эталонного проектируемого объекта в количестве наблюдений, соответствующем принятому числу наблюдений по признакам в комплексе сравнения. Т. е. по 30 значений проектируемой оптимальной длины, 30 значений проектируемого оптимального диаметра, …. массы и т. д. Понятно, что среднее значение этого ряда будет равно каждому частному значению варианты составляющей этот ряд, а дисперсия будет равна «нулю». Вместе с тем для расчета обобщенного среднего по всему комплексу и обобщенного среднего квадратического отклонения для всего комплекса именно такое введение параметров проектируемого эталонного объекта является необходимым. Техническим условием организации такого статистического комплекса является обязательное равенство числа наблюдений каждого из сравниваемых объектов (по каждому отдельному признаку) с числом представительства дат прогнозируемого эталонного объекта в таком сводном комплексе сравнения. Иными словами прогнозируемый эталонный комплекс сравнения должен быть введен в общий комплекс фактических объектов как еще один объект с характеристиками размеров статистических рядов такими же, как и у реальных объектов. Это необходимо для расчета обобщенного среднего всего комплекса с учетом эталона и для учета влияния эталона на обобщенную дисперсию признаков (каждого из них). Т. е. эталонный объект должен быть выбран из общего для всего комплекса, включая и его, параметров объектов, определяющих пределы многомерного статистического пространства в целом, в пределах которого производится комплексное сравнение.

 

ВНИМАНИЕ?

ДОПУЩЕНИЕ 1.

Возможно, здесь допустимо введение значений эталонного объекта как комплекса вариационных рядов с числом наблюдений в каждом равном единице (по одному наблюдению).

 

Допущение 2.

Возможно, что эталонный объект (популяция, сорт, форма и т. п. ) представлен только одной особью с эталонными прогнозируемыми характеристиками. Т. е. в комплекс сравнения реальных объектов (популяций…) вводится эталонный прогнозируемый объект (эталонная прогнозируемая популяция), представленный одной особью (число особей в этой эталонной популяции равно единице, а число наблюдений или замеров признаков на ней рано ранее принятому числу, например 30).

 

Кроме того метод не исключает возможности оценки статистического расстояния в евклидовом пространстве между реальными объектами – реальными популяциями, экотипами, клоновыми группами и т. п. при попарном их сравнении каждого с каждым. В этом случае количество сравнений будет существенно больше, чем при сравнении реальных объектов с эталонным объектом. Существенно важным моментом в этом случае является возникающая возможность оценки статистической близости или удаленности одного объекта от другого по комплексу (из всех анализируемых) признаков. Тогда возникает и возможность оценки генетической близости сравниваемых объектов (при селекционной оценке): т. е. удается установить, какие из объектов наиболее сходны между собой по всему комплексу признаков, а какие – наиболее удалены друг от друга. Принципиально используется схема сравнения, как и при сравнении с эталонным объектом, только в этом случае каждый раз в качестве объекта сравнения поочередно выступает один из реальных объектов, и с ним сравниваются все остальные объекты. В этом случае расчет обобщенного статистического расстояния между реальными объектами при их попарном сравнении будет иметь вид:

 

, где

 

diy = (b_i1-b_y1)²+(b_i2-b_y2)²+(b_i3-b_y3)²+…+(b_ik-b_yk)² ,

 

diy – обобщенное статистическое расстояние между двумя сравниваемыми объектами;

i = 1, 2, 3, …n – индекс порядкового номера одного из двух сравниваемых объектов;

y = 1, 2, 3, …n – индекс порядкового номера другого из двух сравниваемых объектов;

k – количество анализируемых признаков, введенных в комплекс сравнения.

 

Получаемые в итоге такого анализа результаты, представляют собой статистическую оценку обобщенного статистического расстояния между каждой из проанализированных пар объектов. Они неодинаковы, что соответствует различной степени статистической удаленности или близости между конкретными объектами, но при этом, и это очень важно, все полученные оценки сравнимы между собой, поскольку получены для единого многомерного статистического пространства, для одной и той же многомерной системы координат. На основании этого представляется возможным дать обобщенную оценку (единую для всех сравниваемых пар объектов) статистической близости или удаленности сравниваемых объектов: представляется возможным оценить какой из объектов наиболее близок к каждому из других или удален от него. Обобщенное статистическое расстояние измеряется единым критерием, единой единицей измерения общей для всех случаев сравнения объектов. Принципиально это соответствует любому измерению вообще, поскольку измерение есть сравнение с эталоном.

 

При использовании многочисленных признаков (целого комплекса различных признаков) для комплексного сравнительного анализа необходимо выдвижение рабочего условия о равной информативной значимости каждого из анализируемых признаков. В противном случае, когда признаки не равнозначны в информативном плане (существуют более значимые и менее значимые признаки) вводят так называемые коэффициенты ценности признака или весовые коэффициенты.

 

Введение в комплекс сравнения эталонного объекта и оценка статистического расстояния между ним и каждым из реальных объектов позволяет дать оценку каждому из реальных объектов в смысле степени его приближения к эталонному объекту. Возникает возможность ранжировать анализируемые реальные объекты по критерию статистического расстояния между ними и эталонным объектом: чем ближе реальный объект к эталонному объекту, тем выше его оценка в принятой системе оценочных координат (признаков). При этом каждому из реальных объектов присваивается соответствующий ранг (от 1 до n) в зависимости от близости к эталонному объекту (табл. ***).

 

Таблица ***

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: