Методика изучения десятичных дробей.

Перед введением понятия «десятичной дроби» учитель сообщает ученикам, что наибольшее распространение во всём мире получила метрическая система мер.

Достоинством этой системы мер является то, что отношения м/у различными единицами измерения одной и той же величины выражаются степенями числа 10.

При измерении, взвешивании можно например получить число , , 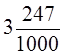т.е. в знаменателе стоят различные степени 10.

Знаменатели данных дробных чисел представляют 1 с нулями. Такие дроби условились записывать без знаменателей. Сначала пишут целую часть, а потом числитель дробной части. Целую часть отделяют от числителя дробной части запятой, при этом числитель дробной части пишут так, чтобы в нём было столько цифр, сколько нулей в знаменателе и учитель снова возвращается к дробным числам: =5,17; =3,247.

Затем объясняются действия над десятичными дробями (для объяснения действия с десятичными дробями исп. индуктивный подход).

Методика изучения обыкновенных дробей.

С понятием дроби учащиеся встречаются в начальной школе, причем программой предусмотрено изучение следующих вопросов: образование дробей; их чтение и запись; числитель и знаменатель дроби, сравнение дробей; нахождение дроби от числа. Главным было формирование у детей конкретно образного представления о дробных числах. Простейшие задачи с дробями решались на основе представлений о дроби, как доли определенной величины. В курсе математики 5 класса, как и в начальной школе, только быстрее ученик должен пройти все этапы наглядного обучения. Вначале непосредственное разбиение предмета на равные части. Затем деление на равные части геометрических фигур на рисунках и чертежах. После этого вводится термин дробь; числитель и знаменатель дроби. Причем понятие дроби вводится описанием. В учебнике приводится рисунок пирога, разрезанного на 4 части, причем одна часть на одной тарелке, три на другой. Говорят, что на одной тарелке лежит четвертая часть пирога, т.е. , на другой тарелке . Такие записи и называются обыкновенными дробями. Рассмотрим дробь . Число 3 называют числителем дроби, 4 - знаменателем. Также необходимо после этого дать характеристику числителю и знаменателю дроби Знаменатель показывает, на сколько частей разделили величину, числитель - сколько взяли частей. Используя рисунки и наглядные предметы, учащиеся знакомятся с понятием равные дроби. Необходимо подчеркнуть, что далее учащиеся встречаются с дробью, как с числом вне всякой связи с частями предмета. Для этого ученикам предлагают задачи такого вида: Прочитайте дроби ; ; 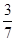;...; запишите в виде дроби число: две третьих, семь десятых,....

Следующим этапом формирования понятия дроби является изображение дробей на луче. Школьникам поясняют, чтобы изобразить дробь 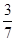надо единичный отрезок разделить на семь частей и отсчитать от начала три таких части.

Затем с помощью координатного луча геометрически интерпретируют понятия «<», «>».

Рассмотрим дроб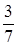и и .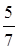

Из двух дробей с одинаковыми знаками больше та, у которой числитель больше.

В 5 классе рассматривается сложение и вычитание дробей с одинаковыми знаменателями. Объяснение нового материала называется с задачи. Буханку хлеба разрезали на 8 равных частей, сначала на тарелку положили 2 части, потом еще 5 частей. На тарелке оказалось части (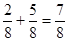). Чтобы сложить дроби с одинаковыми знаменателями, надо к числителю первой дроби прибавить числитель второй дроби, а знаменатель оставить прежним. Аналогично вводится «-».