Методика изучения квадратичной ф-ии

Изучение вопроса о квадратичной функции осуществляется в следующей последовательности, сначала изучается у=2x2. Задача: найти зависимость площади поверхности куба от длинны его ребра. Пусть длинна ребра куба х см, площадь поверхности куба равна 6х2см2, если обозначить х поверхности куба через у, то получаем равенство у=6x2. В рассматриваемой задаче мы встретились с ф-ией, которая задается ф-лой у=ах2, где х – независимая переменная, а – некоторое число. Итак рассмотрим ф-ию у=ах2, выясним что является графиком этой ф-ии, каковы св-ва этой ф-ии:

1) при а=1, у=х2– графиком является парабола.

2) при а=1,5 у=1,5х2. Составляют таблицу, строят график и рассматривая график учащиеся приходят к выводу, что график ф-ии у=1,5х2можно получить из параболы у=х2, растяжением по оси х а полтора раза.

3) при а=0,5, у=0,5 х2– составляют таблицу, аналогично рассматривая график данной ф-ии

приходят к выводу, что график ф-ии у=0,5х2можно получить из параболы у= х2сжатием по оси х в два раза.

4) При а=-0,5, у=-0,5 х2– график ф-ии у=-0,5 х2может быть получен из графика ф-ии у=0,5 х2с помощью симметрии относительно оси х.

Вывод график ф-ии у=ах2при любом значении а≠0 называется параболой, затем:

1) при любом а, если х=0, то у=0 => график ф-ии проходит через начало координат.

2) при a>0, если х≠0, то у>0; при а<0, если х≠0, то у<0 (расположенные в координатной плоскости)

3) противоположным значениям аргумента соответствует равные значения ф-ии, следовательно график ф-ии симметричен относительно оси ординат

4) при a>0, у уменьшается при xє(-∞;0], увеличивается при xє[0;+∞), при а<0, у увеличивается при xє(-∞;0], уменьшается при xє[0;+∞). Точки пересечения параболы с ее осью симметрии называется вершиной параболы

График ф-ии y=ax2+bx+c

Рассматриваются, записанные на доске ф-ии y=x2-15x+8, y=-0,8x2+7x-15, учитель обращает внимание учащихся на то что правые части являются квадратными трехчленами, ф-ии называются квадратичными.

Опр: квадратичной ф-ией называется ф-ия, которую можно задать ф-лой y=ax2+bx+c, где х – независимая переменная, a,b,c – некоторые числа, причем а ≠ 0.

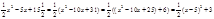Для выяснения, что является графиком квадратичной ф-ии рассматривают пример: . Показывают, что график данной ф-ии может быть получет из графика ф-ии у=½х2с помощью параллельного переноса. Для этого выполняют некоторые преобразования: выделяют квадрат двучлена в правой части: , строят в одной сис-ме координат графики ф-ий у=½х2и у=½(х-5)2+3. Рассмотрим графики данных ф-ий. Учащиеся приходят к выводу, что любая точка графика у=½(х-5)2+3 может быть получена параллельным переносом соответствующих точек графика ф-ии , т.е. парал-ным переносом при котором всякая точка с координатами (х0;y0) переходят в точку с координатами (х0+5;y0+3). Из свойств парал-ного переноса следует, что графиком ф-ии у=½(х-5)2+3, а значит и ф-ии является парабола, равная параболе у=½х2. Далее рассматривают ф-ию в общем виде y=ax2+bx+c. В результате преобразований получают у=а(х+b/2а)2– (b2-4ас)/4а. Эта формула имеет вид y=a(x-m)2+n, m=(-b)/2a, n=(b2-4ас)/4а, можно докь-ть, что график ф-ии y=a(x-m)2+n получился из графика ф-ии y=ax2с помощью пар. переноса при котором точка а с координатами (х0;y0) переходит в точку с координатами (х0+m;y0+n) => графиком ф-ии y=ax2+bx+c является парабола, равная y=ax2, ее вершиной является точка с координатами (m;n).

Для практики удобно строить график квадратичной ф-ии по нескольким точкам: 1) точки с координатами (m,n); 2) точки пересечения с осью Ох: y=0, ; 3) точка пересечения с осью Оу х=0, у=с. Далее рассматривают с-ва ф-ии: область определения ф-ии, область значения ф-ии, монотонность, точки пересечения с координатными осями, промежутки знакопостоянства, наибольшее и наименьшее значение ее.